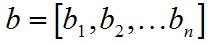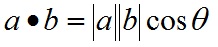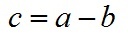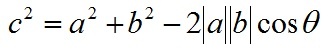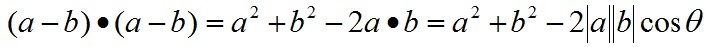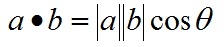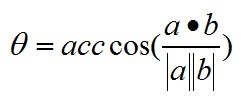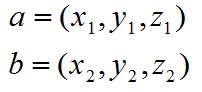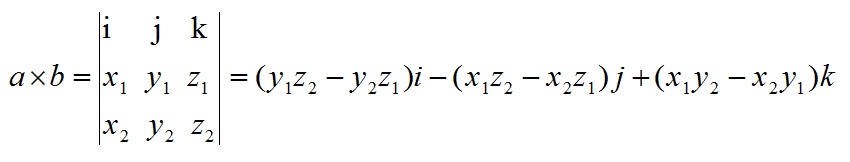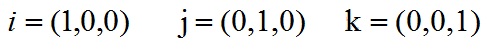向量是由n个实数组成的一个n行1列(n*1)或一个1行n列(1*n)的有序数组;
向量的点乘,也叫向量的内积、数量积,对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个标量。
点乘公式
对于向量a和向量b:
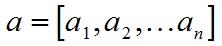
a和b的点积公式为:
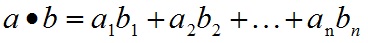
要求一维向量a和向量b的行列数相同。
点乘几何意义
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影,有公式:
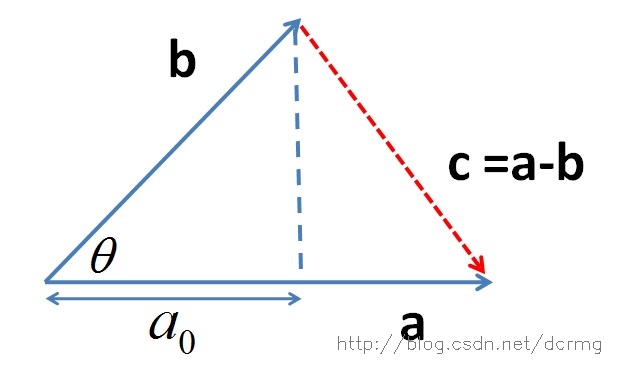
推导过程如下,首先看一下向量组成:
定义向量:
根据三角形余弦定理有:
根据关系c=a-b(a、b、c均为向量)有:
即:
向量a,b的长度都是可以计算的已知量,从而有a和b间的夹角θ:
根据这个公式就可以计算向量a和向量b之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:
a·b>0 方向基本相同,夹角在0°到90°之间
a·b=0 正交,相互垂直
a·b<0 方向基本相反,夹角在90°到180°之间
叉乘公式
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
对于向量a和向量b:
a和b的叉乘公式为:
其中:
根据i、j、k间关系,有:
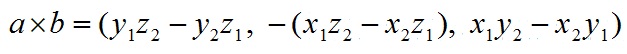
叉乘几何意义
在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
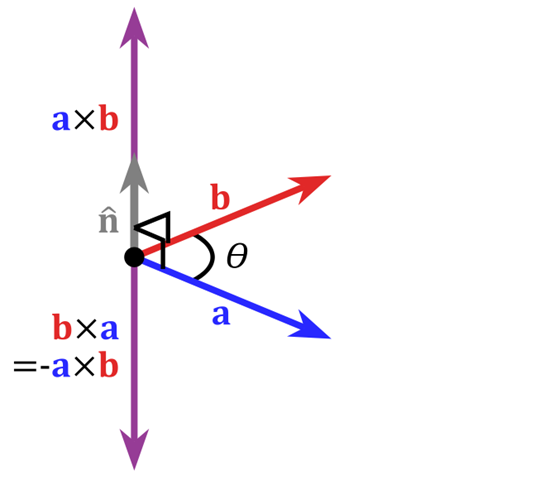
在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
在二维空间中,叉乘还有另外一个几何意义就是:aXb等于由向量a和向量b构成的平行四边形的面积。
向量:u=(u1,u2,u3) v=(v1,v2,v3)
叉积公式:u x v = { u2v3-v2u3 ,u3v1-v3u1 ,u1v2-u2v1 }
点积公式:u * v = u1v1+u2v2+u3v33=lul*lvl*COS(U,V)
对于向量的运算,还有两个“乘法”,那就是点乘和叉乘了.点乘的结果就是两个向量的模相乘,然后再与这两个向量的夹角的余弦值相乘.或者说是两个向量的各个分量分别相乘的结果的和.很明显,点乘的结果就是一个数,这个数对我们分析这两个向量的特点很有帮助.如果点乘的结果为0,那么这两个向量互相垂直;如果结果大于0,那么这两个向量的夹角小于90度;如果结果小于0,那么这两个向量的夹角大于90度.对于叉乘,它的运算公式令人头晕,我就不说了,大家看下面的公式自己领悟吧……
向量c的方向与a,b所在的平面垂直,且方向要用“右手法则”判断(用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向).
若向量a=(a1,b1,c1),向量b=(a2,b2,c2),
则
向量a·向量b=a1a2+b1b2+c1c2
向量a×向量b=
| i j k|
|a1 b1 c1|
|a2 b2 c2|
=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)
(i、j、k分别为空间中相互垂直的三条坐标轴的单位向量).
叉乘的意义就是通过两个向量来确定一个新的向量,该向量与前两个向量都垂直
///计算点积,及向量长度,及向量夹角
double Dot(Vector A,Vector B) { return A.x*B.x+A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A,A)); }
double Angle(Vector A,Vector B) { return acos(Dot(A,B))/Length(A)/Length(B); }
//计算叉积,向量逆时针旋转,两线段是否想交
double Cross(Vector A,Vector B) { return (A.x*B.y-A.y*B.x); }
double Area2(Vector A,Vector B,Vector C) { return Cross(B-A,C-A); }
Vector Rotate(Vector A,double rad)
{
return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
bool Converxline(Vector A,Vector B,Vector C,Vector D)
{
//共线或平行
if((Area2(A,B,C)==0&&Area2(A,B,D)==0) || Area2(A,B,C)*Area2(A,B,D)>0||Area2(C,D,A)*Area2(C,D,B)>0)
return false;
else
return true;
}