Imagine a city with n horizontal streets crossing m vertical streets, forming an (n - 1) × (m - 1) grid. In order to increase the traffic flow, mayor of the city has decided to make each street one way. This means in each horizontal street, the traffic moves only from west to east or only from east to west. Also, traffic moves only from north to south or only from south to north in each vertical street. It is possible to enter a horizontal street from a vertical street, or vice versa, at their intersection.
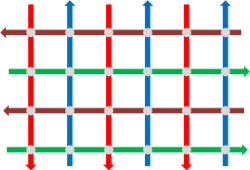
The mayor has received some street direction patterns. Your task is to check whether it is possible to reach any junction from any other junction in the proposed street direction pattern.
The first line of input contains two integers n and m, (2 ≤ n, m ≤ 20), denoting the number of horizontal streets and the number of vertical streets.
The second line contains a string of length n, made of characters '<' and '>', denoting direction of each horizontal street. If the i-th character is equal to '<', the street is directed from east to west otherwise, the street is directed from west to east. Streets are listed in order from north to south.
The third line contains a string of length m, made of characters '^' and 'v', denoting direction of each vertical street. If the i-th character is equal to '^', the street is directed from south to north, otherwise the street is directed from north to south. Streets are listed in order from west to east.
If the given pattern meets the mayor's criteria, print a single line containing "YES", otherwise print a single line containing "NO".
3 3 ><> v^v
NO
4 6 <><> v^v^v^
YES
The figure above shows street directions in the second sample test case.
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define M 1007
using namespace std;
char a[30],b[30];
int head[M],belong[M],dfn[M],low[M],stac[M],vis[M];
int num,cnt,scnt,id;
struct E
{
int v,next;
}edg[M*M];
void addedge(int u,int v)
{
edg[num].v=v;
edg[num].next=head[u];
head[u]=num++;
}
void init()
{
num=cnt=scnt=id=0;
memset(vis,0,sizeof(vis));
memset(head,-1,sizeof(head));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
}
void tarjan(int x)
{
int v;
dfn[x]=low[x]=++cnt;
stac[id++]=x;
vis[x]=1;
for(int u=head[x];u!=-1;u=edg[u].next)
{
int v=edg[u].v;
if(!dfn[v]){tarjan(v);low[x]=min(low[x],low[v]);}
else if(vis[v])low[x]=min(low[x],dfn[v]);
}
if(low[x]==dfn[x])
{
scnt++;
do
{
v=stac[--id];
belong[v]=scnt;
vis[v]=0;
}while(v!=x);
}
}
int main()
{
int n,m;
while(scanf("%d%d",&n,&m)!=EOF)
{
init();
scanf("%s%s",a+1,b+1);
for(int i=1;i<=n;i++)
{
int s=(i-1)*m;
if(a[i]=='>')
for(int j=1;j<m;j++)addedge(s+j,s+j+1);
else
for(int j=m;j>1;j--)addedge(s+j,s+j-1);
}
for(int i=1;i<=m;i++)
{
int s=i;
if(b[i]=='v')
for(int j=1;j<n;j++)addedge(s+(j-1)*m,s+j*m);
else
for(int j=n;j>1;j--)addedge(s+(j-1)*m,s+(j-2)*m);
}
for(int i=1;i<=n*m;i++)
if(!dfn[i])
tarjan(i);
if(scnt==1)printf("YES
");
else printf("NO
");
}
return 0;
}