二分查找插入排序以及一些思考

　　二分查找的插入排序是在处理待处理插入元素时，在已排好序的集合中采用二分法查找到插入的位置，而后进行整体后移，腾出这个插入的位置后，将该元素插入。

　　思路并不难理解，但是当我面对这个二分法实现的时候，还是觉得有很多细节不好处理，于是有了以下思路的记录：

定义i为当前轮到的比较元素，如果i<2，那么不需要比较，直接返回。
1.确定顺序集合的边界
　　从0到i-1
2.确定中点位置
　　如果是奇数：从0开始算是偶数个元素，所以无法确定到真正的中位，只能中位最近的两个元素取一个，(i-1-0)/2满足条件
　　如果是偶数：从0开始算是奇数个元素，(i-1-0)/2就是真正的中位元素，满足条件
　　这个结论对于非0开始的元素也是成立的
　　所以，设定开始(include)进行计数的边界为start,结束(include)计数的边界为(i-1)，那么((i-1-start)/2)+start就是中点位置元素
3.一般情况
　　第一轮比较，0和i-1计算出中点位置为k=(i-1-0)/2，将i位置与k位置进行比较
　　如果i位置元素更大，那么下一轮比较的范围是k+1,i-1；
　　如果i位置元素更小，那么下一轮比较的范围是0,k-1;
　　如果i位置元素相等，那么此时就得到了i的插入位置为k+1,原k+1位置到i-1位置全部后移一个位置。
　　第二轮比较，计算出中点位置为k1=((i-1-k-1)/2)+k+1，将i位置与k1位置进行比较
　　...
4.边界情况
　　在步骤3中，讨论的是正常比较和推进的策略，这里步骤4讨论的是比较的终止条件。
　　在步骤3中已经讨论了一种插入情况，就是找到了与i元素相等元素的位置时，可以插入；但是，如果整个序列里没有相等的情况，我们就需要用边界去比较得到最终的插入位置。
　　计数和偶数序列的最后一次二分判断情况应该如下图所示：

 

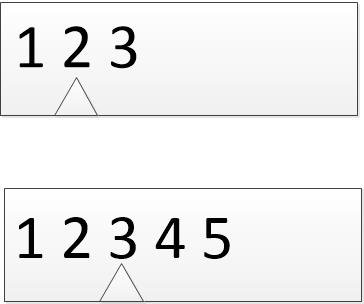
　　如果剩余的是1个元素，即边界[m,n]中，m==n，此时只需要判断i位置元素与这个元素的大小就能确定插入位置：
　　如果小于等于该剩余元素，那么插入位置为m;
　　否则插入位置为m+1;

　　如果剩余的是2个元素，即边界[m,n]中，m+1==n，那么此时需要根据与这两个元素的比较结果确定插入位置：
　　<=左侧元素，那么插入位置为m;
　　>=右侧元素，那么插入位置为n+1;

　　同时不满足以上两点，那就证明这个元素的值介于左右侧元素之间，且都不相等，那么插入位置为m+1;
　　如果剩余的是3个及以上，那么还可以进行再次的二分判断逻辑。

　综合上面的分析，逻辑编写时，while的判定条件应该就是m和n的关系来确定。先进行m与n的关系判断，而后内部的循环应该是靠不断地改变边界来推动比较过程，最终确定插入位置。
　注意，这里是可以写成一个递归函数的，但是能用while搞定就尽量不要用递归，因为递归还需要考虑栈深。
　另外，由于查找到了插入位置后，后续的位置交换也是固定的，此时可以从i-1位开始向前推进，每一位都往后一位覆盖，一直到插入的位置，不用再进行交换操作。
　以上其实是一种分析二分法的套路，也可以算作一种分析比较复杂情况的分析套路。

=================================================================　　

　　　代码经过编写调试如下：

public class BinarySearchInsertionSort {
    public static void sort(int[] array) {
        if (array == null || array.length < 2) {
            return;
        }

        int start = 0;
        int end = 0;
        int insert = 0;
        for (int i = 0; i < array.length - 1; i++) {
            //1.找到已排好的序列，找到需要进行插入的元素
            //待处理的元素如果已经超过范围，说明排序已经完成，可以退出循环
            int process = end + 1;
            if (process > array.length - 1) {
                break;
            }

            //比较待二分处理的序列，如果序列长度超过2，才进行二分处理
            boolean findLocation = false;
            while (end - start >= 2) {
                //进行二分处理，找到插入位置
                int middle = start + ((end - start) / 2);
                if (array[process] == array[middle]) {
                    insert = middle + 1;
                    findLocation = true;
                    break;
                } else if (array[process] > array[middle]) {
                    start = middle + 1;
                } else {
                    end = middle - 1;
                }
            }
            if (!findLocation) {
                //如果到这里，说明本身序列长度不超过2个；或者，在while中没有找到相等的middle位置
                insert = findInsertLocationForLessEqualTwo(array, start, end, insert, process);
            }

            //2.找到了插入位置，这里进行元素的后移
            int readyInsertValue = array[process];
            for (int j = process; j > insert; j--) {
                array[j] = array[j - 1];
            }
            array[insert] = readyInsertValue;

            //3.确定下一个元素二分查找的start与end位置
            start = 0;
            end = i + 1;
        }
    }

    private static int findInsertLocationForLessEqualTwo(int[] array, int start, int end, int insert, int process) {
        if (start == end) {
            if (array[process] <= array[start]) {
                insert = start;
            } else {
                insert = start + 1;
            }
        } else if (start + 1 == end) {
            if (array[process] <= array[start]) {
                insert = start;
            } else if (array[process] >= array[end]) {
                insert = end + 1;
            } else {
                insert = start + 1;
            }
        } else {
            throw new RuntimeException("logic error");
        }
        return insert;
    }

    public static void main(String[] args) {
        int[] array = {2, 3, 1, 4, 2, 44, 32, 13, 12, 56, 32, 12, 33, 21, 15, 16, 76, 45, 32, 33, 121, 123, 123, 122};
        sort(array);
        System.out.println("Arrays.toString(array) = " + Arrays.toString(array));
    }
}

　　这里需要注意的是，二分查找只是将查找的效率提高了，但是在一轮插入最坏的情况下，还是会出现n-1次元素赋值操作，所以算法复杂度没有根本变化。最优时O(n)，最差时O(n^2)。

=================================================================

　　在整理这个思路的过程中，我愈发觉得，其实要思考了整个过程，才能形成一些自己的套路。就像熟悉了一个有序集合可以使用二分法，也像单轴快排与双轴快排对比，会发现双周快排其实是一个轮次做了更多的事情，这样的思路可能会让我们在新场景旧问题的情况下很快形成解决思路，而对于这种本质的把控，可能真的需要我们将整个逻辑在脑子里不断地放电影，形成动图，才有可能实现。