在之前的两篇blog中,已经简要的说明了冒泡排序和快排的原理、过程图示以及代码实现。这里主要讨论的是两种排序的复杂度以及一些常见的优化手段。
冒泡排序
【时间复杂度】
在整个序列完全是有序的状态下,只需要执行第一次的内层循环。只要做好标记,我们就不用再进行后续的内层循环。此时时间复杂度为O(n);
再来计算最坏的情况。外层的循环每次都进行,那么会进行N次,而这N轮的比较次数分别是(n-1),(n-2),(n-3),(n-4)...1,0,所以总的比较次数为(0+1+2+...+n-1)=n*(n-1)/2,所以根据O法则,它的时间复杂度为O(n^2)。
【空间复杂度】
整个冒泡排序过程中,只用了一个可以重复利用的临时变量,用于交换需要调换位置的元素,所以空间复杂度为O(1)。
【稳定性】
所谓的稳定性,就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。冒牌排序是可以保证两个相等元素前后的排列顺序不发生变化。所以冒泡排序是稳定的。
【时间复杂度的平均情况】
其实最好最坏的情况都不难分析,但是平均情况的排序需要考虑的就是,n个元素的序列所有可能的情况下(即n!),时间复杂度的一个加权平均期望时间复杂度,需要结合概率论的知识,严格定量的推导是很复杂的。
这里可以稍微想想,这n!中排序的情况,顺序和逆序的情况应该是对称的。比如说,1和2,有[1,2]这个顺序,就会有[2,1]这个顺序;1,2,3三个元素,有[1,2,3]这个顺序,就会有[3,2,1]这个顺序。而冒泡排序中,我们可以想到的是,如果完全顺序,就是n-1次,而完全逆序,就是n(n-1)/2次,其它的情况,可以想到随着这种顺序的程度,从完全顺序到完全逆序不断地转换,那么这个次数应该是一个线性地变化过程。所以可以认为,这个平均值接近最差情况的一半,所以平均时间复杂度可以认为是O(n^2) 。
快速排序
【时间复杂度】
在整个序列完全有序,以及完全相等的情况下,每一次R的位置,从集合的最右侧,经过n-1次滑动到L的位置,最终确定pivot(加入pivot每次取最左侧的元素)不再参与下一轮的快排。那么,整个排序完成,会发生的快排操作次数为(n-1)+(n-2)+...+1=n(n-1)/2,与冒泡排序的最差情况一致。时间复杂度为O(n^2)。
这里用公式进行归纳,也可以得到最差的情况,公式比较难打,这里手写拍照用图片记录了:
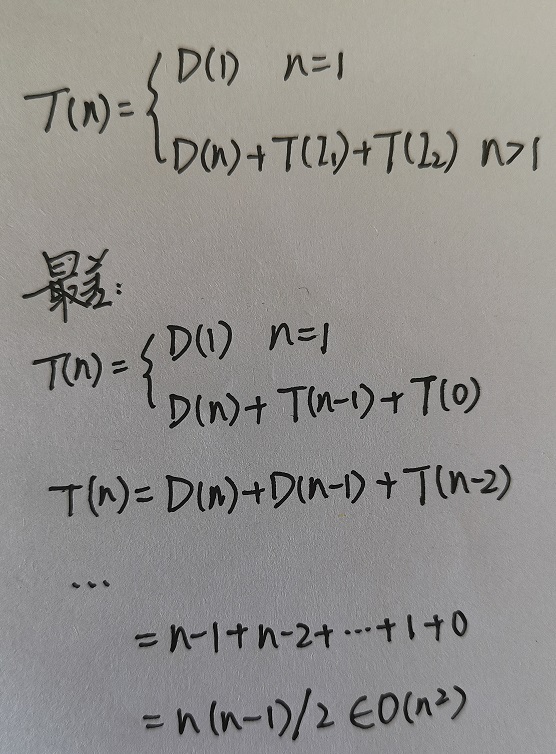
用同样的方法,我们来推导最优的情况。尽管网上有直接给出情况是O(nlog(2)n),但是很少有将过程说清楚的。这里给出推导过程:

平均复杂度的情况更加复杂,这里就不进行推导了。最终的结果,平均复杂度也是O(nlog(2)n)。
【空间复杂度】
快排过程中,不需要临时空间进行存储元素,在原数组上就能完成,但是由于快排是递归调用,所以会消耗函数调用栈空间。在分区选择最优的情况下,栈深度为log(2)n,所以空间复杂度最优为O(log(2)n),最差情况深度会变为n,所以复杂度为O(n)。平均情况下,递归深度也是对数级别的。
【稳定性】
由于pivot选择不同会导致原数组中相同元素的位置不同(考虑用不同位置的同值元素作为pivot),所以快排并不稳定。