原文网址:https://zhuanlan.zhihu.com/p/428783752
1、时域(时间域)(time domain)
自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x(t)是描述信号在不同时刻取值的函数。
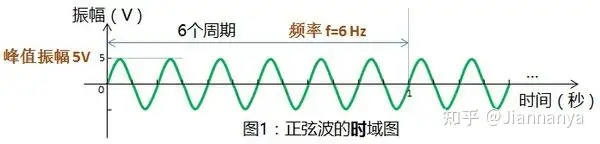
图1是正弦波的时域图,示出了振幅与时间的关系。在时域图中,横轴是时间,纵轴是振幅。时域图显示振幅随时间的变化,可以看出峰值振幅为5V,可以算出频率f=6 Hz。
2、频域(频率域)(frequency domain)
自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。

图2是图1中正弦波的频域图,在频域图中,横轴是频率,纵轴是峰值振幅。频域图仅仅示出峰值振幅与频率,而不显示振幅随时间的变化。
从频域图可以看出,正弦波的频率为6Hz,这个6Hz的正弦波的峰值振幅为5V 。
频域图的优点是,从频域图中,可以一眼看出正弦波的频率和峰值振幅。整个正弦波在频域图上只是一个立柱立柱的位置显示了正弦波的频率,立柱的高度显示了正弦波的峰值振幅。
3、时域和频域
将时域频域一起放在一个三维的坐标系中,如图所示,与时域和频域的轴表示振幅:
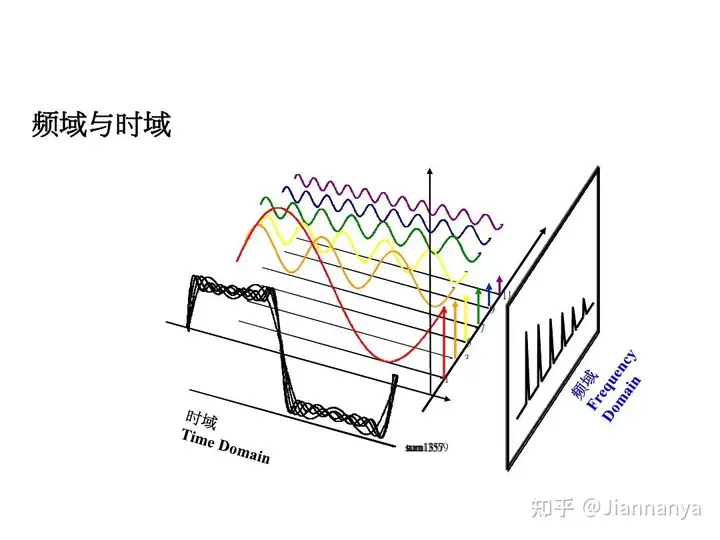
另外一张动图:
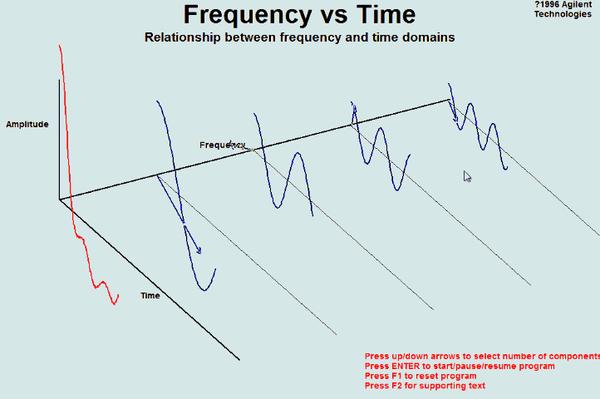
4、时域变换到频域的意义
对信号进行时域分析时,有时一些信号的时域参数相同,但并不能说明信号就完全相同。因为信号不仅随时间变化,还与频率、相位等信息有关,这就需要进一步分析信号的频率结构,并在频率域中对信号进行描述。
动态信号从时间域变换到频率域主要通过傅立叶级数和傅立叶变换等来实现。很简单时域分析的函数是参数是t,也就是y=f(t),频域分析时,参数是w,也就是y=F(w)两者之间可以互相转化。时域函数通过傅立叶或者拉普拉斯变换就变成了频域函数。
总的来说,在某种需求下将信号变换到另一种域中,有利于进行处理、计算和分析。
5、空间域(spatial domain)
空间域简称空域,又称图像空间(image space),一般这个概念会出现在数字图像处理中,指由图像像元组成的空间。在图像空间中以长度(距离)为自变量直接对像元值进行处理称为空间域处理。
实际上你可以简单理解为,像素空间,在空域的处理就是在像素级的处理,通过傅立叶变换后,得到的是图像的频谱。表示图像的能量梯度。