迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止
###基本思想
-
通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
-
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
-
初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 … 重复该操作,直到遍历完所有顶点。
###操作步骤
-
初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
-
从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
-
更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
-
重复步骤(2)和(3),直到遍历完所有顶点。
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
###图解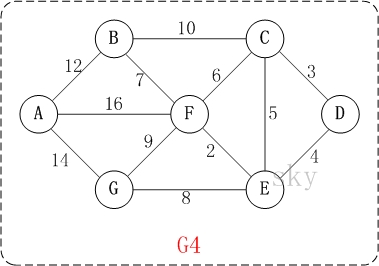
以上图G4为例,来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。以下B节点中23应为13。
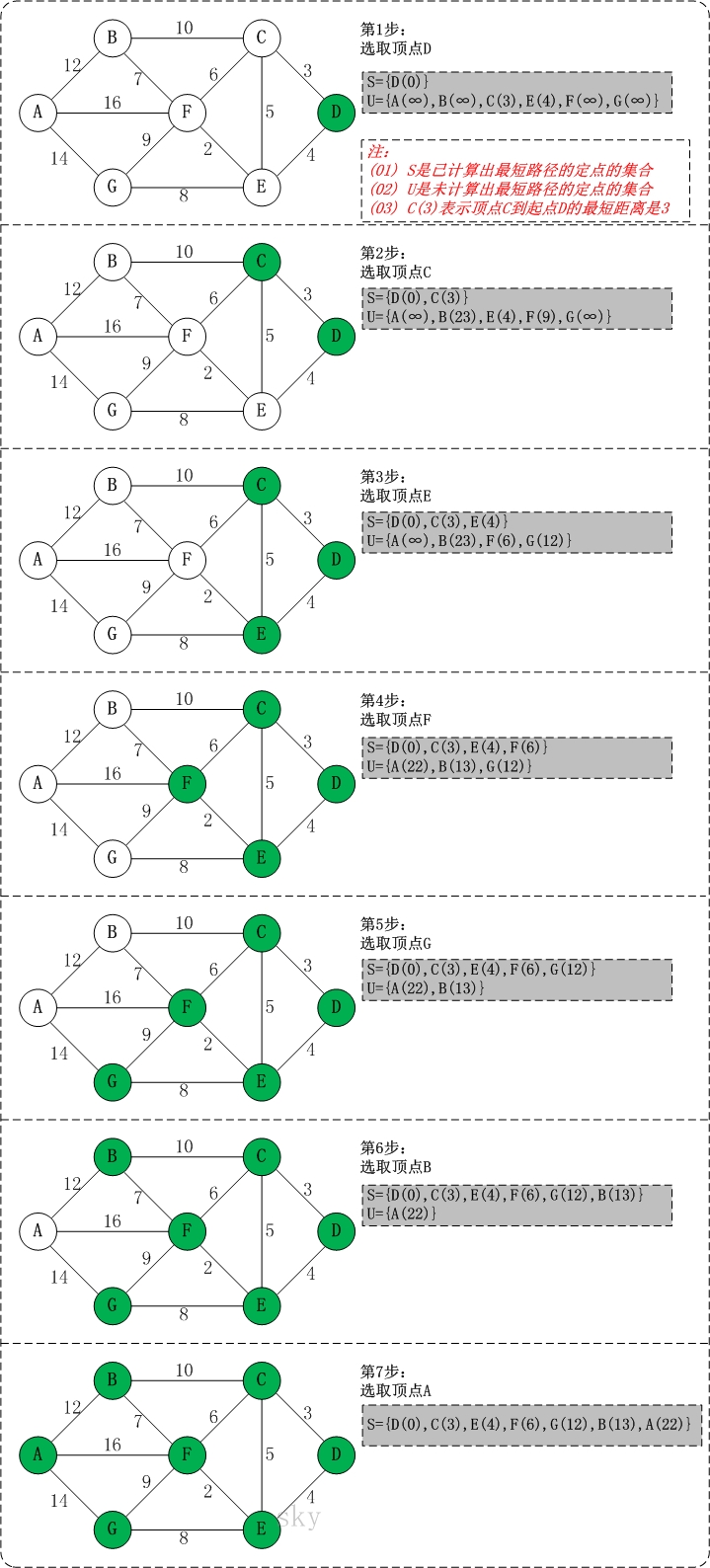
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。
###代码
邻接矩阵为例,
// 邻接矩阵
typedef struct _graph
{
char vexs[MAX]; // 顶点集合
int vexnum; // 顶点数
int edgnum; // 边数
int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;
// 边的结构体
typedef struct _EdgeData
{
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
}EData;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
Graph是邻接矩阵对应的结构体。
vexs用于保存顶点,vexnum是顶点数,edgnum是边数;matrix则是用于保存矩阵信息的二维数组。
例如,matrix[i][j]=1,则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点;matrix[i][j]=0,则表示它们不是邻接点。
EData是邻接矩阵边对应的结构体。
####Dijkstra算法
/*
* Dijkstra最短路径。
* 即,统计图(G)中"顶点vs"到其它各个顶点的最短路径。
*
* 参数说明:
* G -- 图
* vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。
* prev -- 前驱顶点数组。即,prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中,位于"顶点i"之前的那个顶点。
* dist -- 长度数组。即,dist[i]是"顶点vs"到"顶点i"的最短路径的长度。
*/
void dijkstra(Graph G, int vs, int prev[], int dist[])
{
int i,j,k;
int min;
int tmp;
int flag[MAX]; // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。
// 初始化
for (i = 0; i < G.vexnum; i++)
{
flag[i] = 0; // 顶点i的最短路径还没获取到。
prev[i] = 0; // 顶点i的前驱顶点为0。
dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。
}
// 对"顶点vs"自身进行初始化
flag[vs] = 1;
dist[vs] = 0;
// 遍历G.vexnum-1次;每次找出一个顶点的最短路径。
for (i = 1; i < G.vexnum; i++)
{
// 寻找当前最小的路径;
// 即,在未获取最短路径的顶点中,找到离vs最近的顶点(k)。
min = INF;
for (j = 0; j < G.vexnum; j++)
{
if (flag[j]==0 && dist[j]<min)
{
min = dist[j];
k = j;
}
}
// 标记"顶点k"为已经获取到最短路径
flag[k] = 1;
// 修正当前最短路径和前驱顶点
// 即,当已经"顶点k的最短路径"之后,更新"未获取最短路径的顶点的最短路径和前驱顶点"。
for (j = 0; j < G.vexnum; j++)
{
tmp = (G.matrix[k][j]==INF ? INF : (min + G.matrix[k][j])); // 防止溢出
if (flag[j] == 0 && (tmp < dist[j]) )
{
dist[j] = tmp;
prev[j] = k;
}
}
}
// 打印dijkstra最短路径的结果
printf("dijkstra(%c):
", G.vexs[vs]);
for (i = 0; i < G.vexnum; i++)
printf(" shortest(%c, %c)=%d
", G.vexs[vs], G.vexs[i], dist[i]);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
###参考资料
1, http://www.cnblogs.com/skywang12345/p/3711512.html