经典树与图论（最小生成树、哈夫曼树、最短路径问题---Dijkstra算法）

参考网址： https://www.jianshu.com/p/cb5af6b5096d

算法导论--最小生成树

最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

image.png

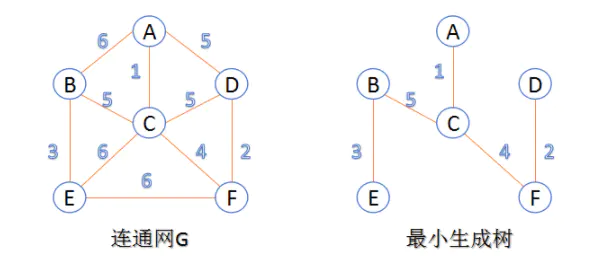
1.Kruskal算法
此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

1. 把图中的所有边按代价从小到大排序；
2. 把图中的n个顶点看成独立的n棵树组成的森林；
3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。

4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

   
   
    

   

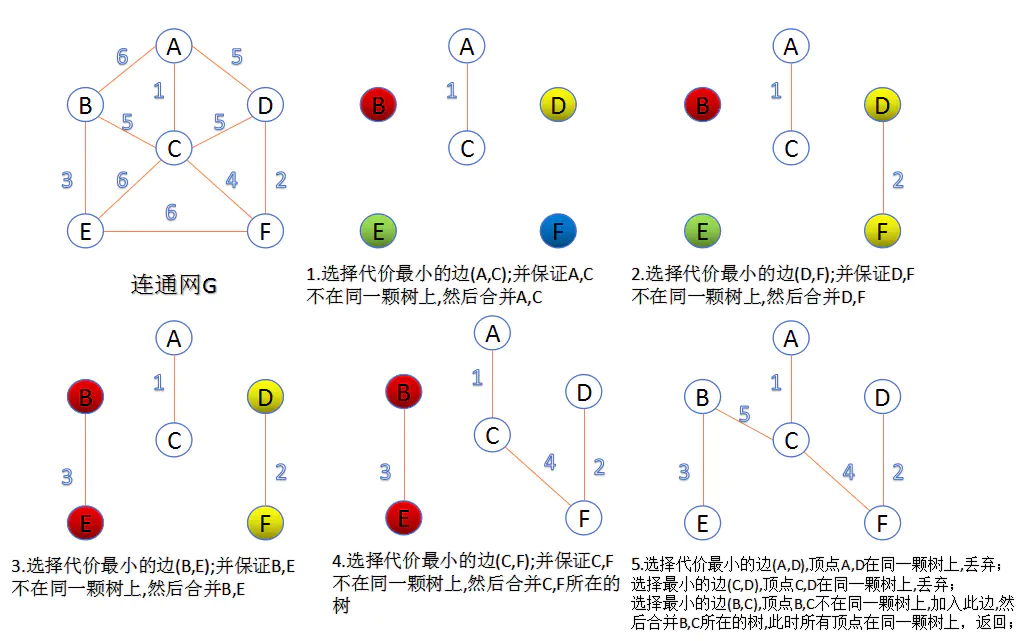   image.png

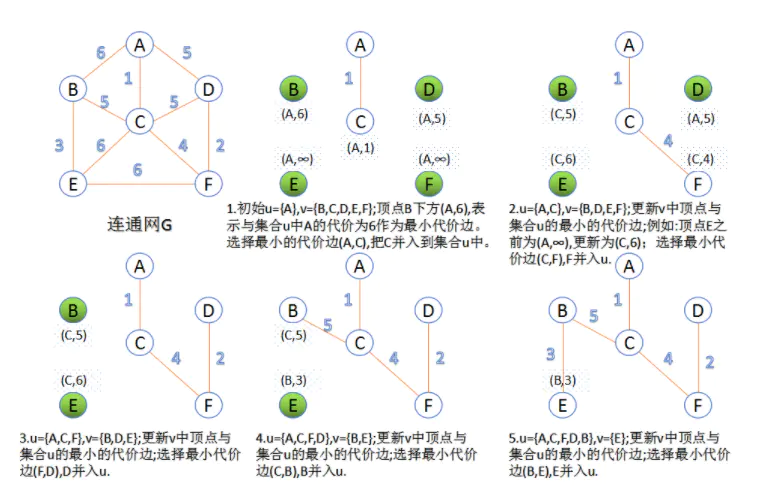
Prim算法
此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1.图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;
2.在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。
3.重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

 

 

image.png

哈夫曼树

哈夫曼树又称最优二叉树。它是 n 个带权叶子结点构成的所有二叉树中，带权路径长度 WPL 最小的二叉树。

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：
(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；
(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
(3)从森林中删除选取的两棵树，并将新树加入森林；
(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

 

image.png

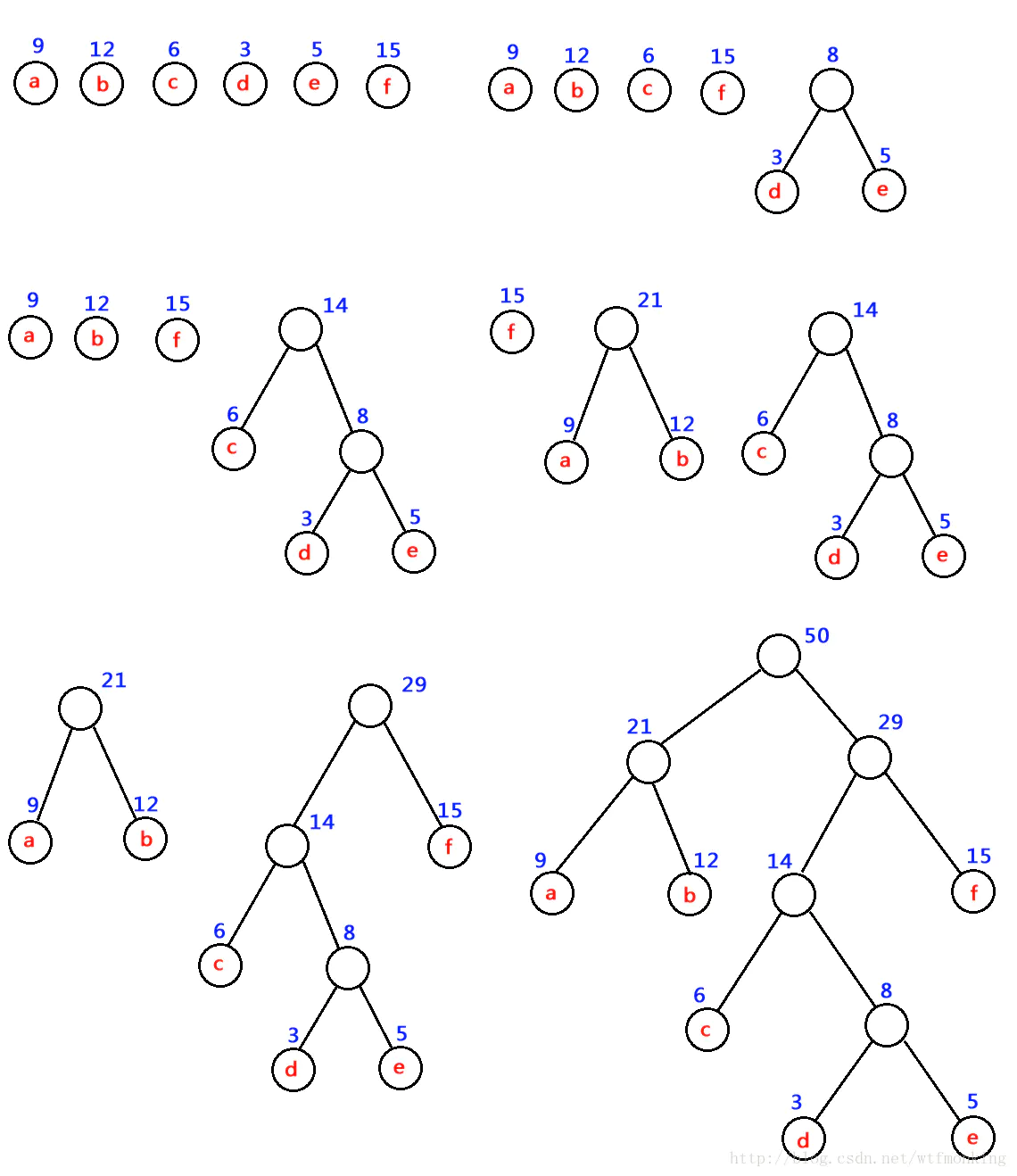
注意：为了使得到的哈夫曼树的结构尽量唯一，通常规定生成的哈夫曼树中每个结点的左子树根结点的权小于等于右子树根结点的权。

哈夫曼编码

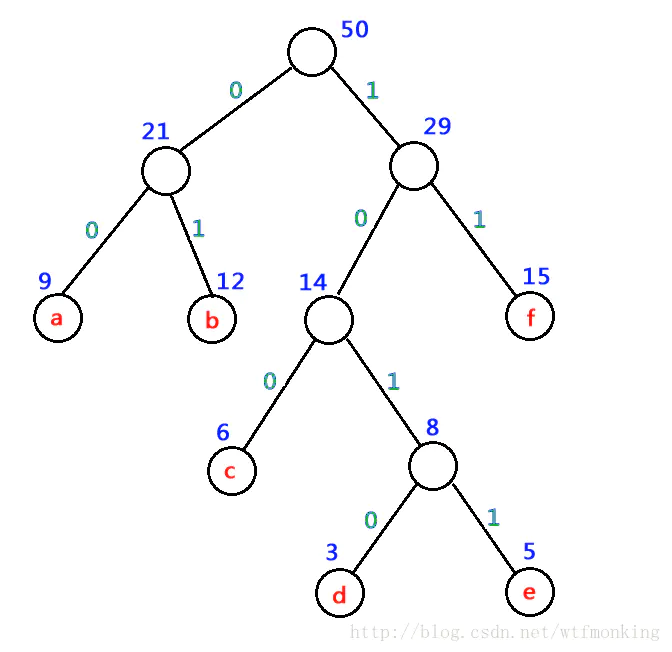
在电报通信中，电文是以二进制的0、1序列传送的，每个字符对应一个二进制编码，为了缩短电文的总长度，采用不等长编码方式，构造哈夫曼树，
将每个字符的出现频率作为字符结点的权值赋予叶子结点，每个分支结点的左右分支分别用0和1编码，从树根结点到每个叶子结点的路径上
所经分支的0、1编码序列等于该叶子结点的二进制编码。如上文所示的哈夫曼编码如下：

 

image.png

最短路径问题---Dijkstra算法

最短路径问题介绍
问题解释：
从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径。

 

 

image.png

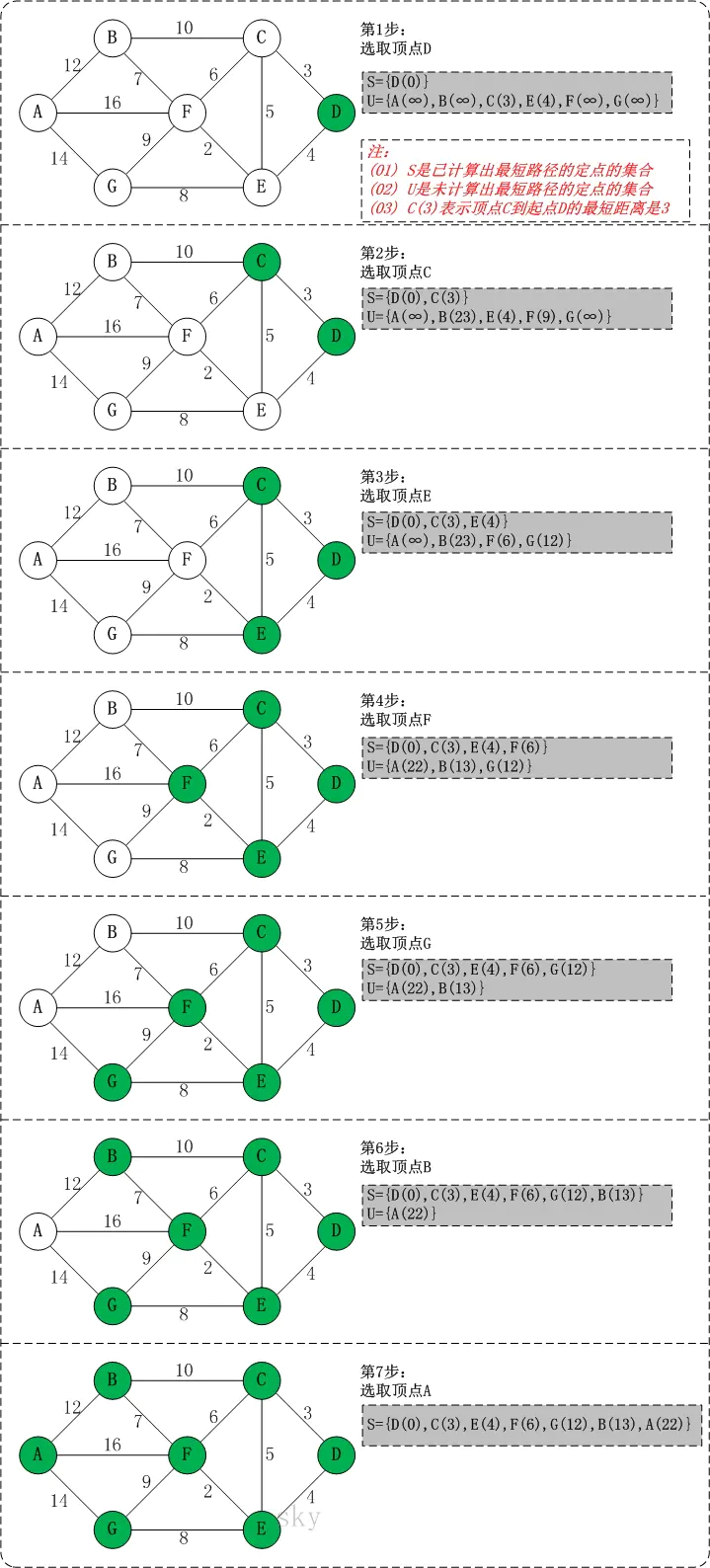
初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！
第1步：将顶点D加入到S中。
此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。
上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。
此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。
上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。
此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。
此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

作者：第六象限
链接：https://www.jianshu.com/p/cb5af6b5096d
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。