查找算法

博客园：数据结构

目录

• 1. 顺序查找
• 2. 二分查找
  • 2.1. 二分查找框架
  • 2.2. 二分查找针对的是有序数据
  • 2.3. 数据量太小不适合二分查找
  • 2.4. 数据量太大不适合二分查找
  • 2.5. 折半查找算法只适用于有序表，同时仅限于查找表用顺序存储结构表示
• 3. 索引顺序查找（分块查找）算法
  • 3.1. 分块查找的性能分析
• 4. 静态树表查找算法
  • 4.1. 次优查找树的构建方法
  • 4.2. 完整示例演示
  • 4.3. 总结
• 5. 动态查找表：二叉排序树（二叉查找树）
  • 5.1. 什么是二叉排序树？
  • 5.2. 使用二叉排序树查找关键字
  • 5.3. 二叉排序树中插入关键字
  • 5.4. 二叉排序树中删除关键字
  • 5.5. 总结

1. 顺序查找

顺序查找没有难度和技术含量，是我们谁都能想到并且最先会想到一种最直接的方法。比如在玩扑克牌的时候，若不需要大小王，则我们会拿过来所有的牌，从头到尾地一张一张地找。

我们有时需要显示一些人的详细信息，比如榜单，我们往往在排行榜中只保存了用户id与得分数，这时可以根据得分数获取前 10 名用于展示，可是我们不知道这些 id 对应哪个人，所以往往还需要用户的一些其他信息如昵称、头像等。

这时我设计了这样一段代码逻辑：先找出前 10 名的 id，再查出这 10 个人的详细信息列表，然后循环这 10 个人的 id，内层循环这 10 个人的详细信息，发现 id 一致时，我们就可以找到对应的某个人的详细信息了。这里就是典型的顺序查找。

顺序查找由于其简单的特点，在元素并不多的很多情况下，运用还是很广泛的。因为没有必要为了有限数量的元素使用复杂的算法。

2. 二分查找

五分钟学算法：二分查找算法详解

先给大家讲个笑话乐呵一下：

有一天阿东到图书馆借了 N 本书，出图书馆的时候，警报响了，于是保安把阿东拦下，要检查一下哪本书没有登记出借。阿东正准备把每一本书在报警器下过一下，以找出引发警报的书，但是保安露出不屑的眼神：你连二分查找都不会吗？于是保安把书分成两堆，让第一堆过一下报警器，报警器响；于是再把这堆书分成两堆…… 最终，检测了 log2N 次之后，保安成功的找到了那本引起警报的书，露出了得意和嘲讽的笑容。于是阿东背着剩下的书走了。

从此，图书馆丢了 N – 1 本书。

二分查找真的很简单吗？并不简单。看看 Knuth 大佬（发明 KMP 算法的那位）怎么说的：

Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky…

这句话可以这样理解：思路很简单，细节是魔鬼。

2.1. 二分查找框架

int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = (right + left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。本文都会使用 else if，旨在讲清楚，读者理解后可自行简化。

其中…标记的部分，就是可能出现细节问题的地方，当你见到一个二分查找的代码时，首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。

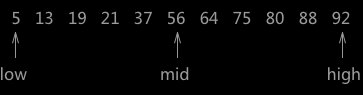
2.2. 二分查找针对的是有序数据

二分查找需要的数据必须是有序的。如果数据没有序，我们需要先排序，排序的时间复杂度最低是 O(nlogn)。所以，如果我们针对的是一组静态的数据，没有频繁地插入、删除，我们可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较低。

但是，如果我们的数据集合有频繁的插入和删除操作，要想用二分查找，要么每次插入、删除操作之后保证数据仍然有序，要么在每次二分查找之前都先进行排序。针对这种动态数据集合，无论哪种方法，维护有序的成本都是很高的。

所以，二分查找只能用在插入、删除操作不频繁，一次排序多次查找的场景中。针对动态变化的数据集合，二分查找将不再适用

2.3. 数据量太小不适合二分查找

如果要处理的数据量很小，完全没有必要用二分查找，顺序遍历就足够了。比如我们在一个大小为 10 的数组中查找一个元素，不管用二分查找还是顺序遍历，查找速度都差不多，只有数据量比较大的时候，二分查找的优势才会比较明显。

2.4. 数据量太大不适合二分查找

二分查找底层依赖的是数组，数组需要的是一段连续的存储空间，所以我们的数据比较大时，比如1GB，这时候可能不太适合使用二分查找，因为我们的内存都是离散的，可能电脑没有这么多的内存。

2.5. 折半查找算法只适用于有序表，同时仅限于查找表用顺序存储结构表示

当查找表使用链式存储结构表示时，折半查找算法无法有效地进行比较操作（排序和查找操作的实现都异常繁琐）。

3. 索引顺序查找（分块查找）算法

将n个数据元素按块有序的划分为m块（m不能大于n）。每一块的元素可以不是有序的，但块与块之间必须有序。第一块中的任一元素的关键字都必须小于第二块任一元素的关键字，第二块中的任一元素都要小于第三块中的任一元素······

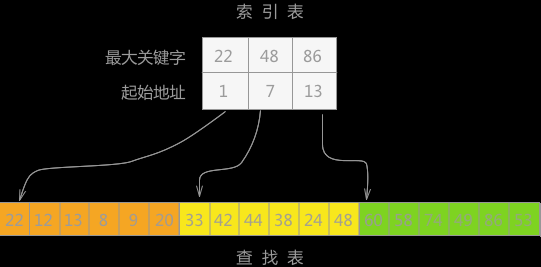
具体操作

1. 先在各块的最大关键字构成索引表。
2. 查找分为两部分，先对索引表进行二分查找或顺序查找，已确定待查记录在哪一块中。
3. 然后，在已经确实的块中用顺序法进行查找。注意这里的这一步只能用顺序法。

3.1. 分块查找的性能分析

分块查找算法的运行效率受两部分影响：查找块的操作和块内查找的操作。查找块的操作可以采用顺序查找，也可以采用折半查找（更优）；块内查找的操作采用顺序查找的方式。相比于折半查找，分块查找时间效率上更低一些；相比于顺序查找，由于在子表中进行，比较的子表个数会不同程度的减少，所有分块查找算法会更优。

总体来说，分块查找算法的效率介于顺序查找和折半查找之间。

4. 静态树表查找算法

博客园: 静态树表查找算法

前面章节所介绍的有关在静态查找表中对特定关键字进行顺序查找、折半查找或者分块查找，都是在查找表中各关键字被查找概率相同的前提下进行的。

例如查找表中有 n 个关键字，表中每个关键字被查找的概率都是 1/n。在等概率的情况，使用折半查找算法的性能最优。

而在某些情况下，查找表中各关键字被查找的概率是不同的。例如水果商店中有很多种水果，对于不同的顾客来说，由于口味不同，各种水果可能被选择的概率是不同的。假设该顾客喜吃酸，那么相对于苹果和橘子，选择橘子的概率肯定要更高一些。

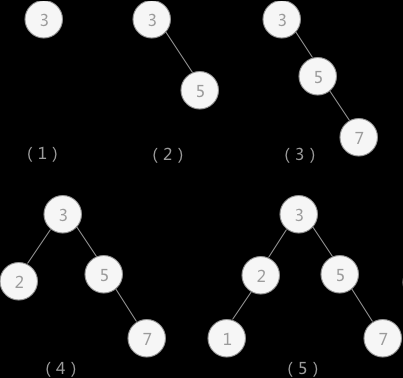
在查找表中各关键字查找概率不相同的情况下，对于使用折半查找算法，按照之前的方式进行，其查找的效率并不一定是最优的。例如，某查找表中有 5 个关键字，各关键字被查找到的概率分别为：0.1，0.2，0.1，0.4，0.2（全部关键字被查找概率和为 1 ），则根据之前介绍的折半查找算法，建立相应的判定树为（树中各关键字用概率表示）：

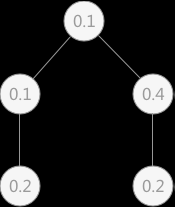
折半查找查找成功时的平均查找长度的计算方式为： ASL = 判定树中各结点的查找概率*所在层次

所以该平均查找长度为： ASL=0.1*1 + 0.1*2 + 0.4*2 + 0.2*3 + 0.2*3 = 2.3

由于各关键字被查找的概率是不相同的，所以若在查找时遵循被查找关键字先和查找概率大的关键字进行比对，建立的判定树为：

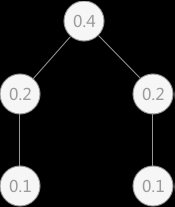
相应的平均查找长度为： ASL=0.4*1 + 0.2*2 + 0.2*2 + 0.1*3 + 0.1*3=1.8

后者折半查找的效率要比前者高，所以在查找表中各关键字查找概率不同时，要考虑建立一棵查找性能最佳的判定树。若在只考虑查找成功的情况下，描述查找过程的判定树其带权路径长度之和（用 PH 表示）最小时，查找性能最优，称该二叉树为静态最优查找树。

带权路径之和的计算公式为： PH = 所有结点所在的层次数 * 每个结点对应的概率值

但是由于构造最优查找树花费的时间代价较高，而且有一种构造方式创建的判定树的查找性能同最优查找树仅差 1% - 2%，称这种极度接近于最优查找树的二叉树为次优查找树。

4.1. 次优查找树的构建方法

首先取出查找表中每个关键字及其对应的权值，采用如下公式计算出每个关键字对应的一个值：

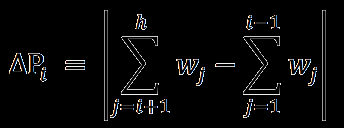
其中 wj 表示每个关键字的权值（被查找到的概率），h 表示关键字的个数。

表中有多少关键字，就会有多少个 △Pi ，取其中最小的做为次优查找树的根结点，然后将表中关键字从第 i 个关键字的位置分成两部分，分别作为该根结点的左子树和右子树。同理，左子树和右子树也这么处理，直到最后构成次优查找树完成。

4.2. 完整示例演示

例如，一含有 9 个关键字的查找表及其相应权值如下表所示：

则构建次优查找树的过程如下：

首先求出查找表中所有的 △P 的值，找出整棵查找表的根结点：

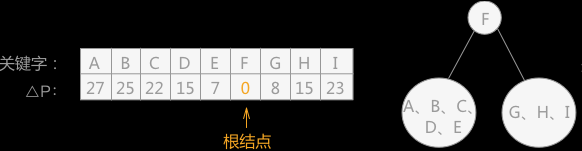
例如，关键字 F 的 △P 的计算方式为：从 G 到 I 的权值和 - 从 A 到 E 的权值和 = 4+3+5-1-1-2-5-3 = 0。

通过上图左侧表格得知，根结点为 F，以 F 为分界线，左侧子表为 F 结点的左子树，右侧子表为 F 结点的右子树（如上图右侧所示），继续查找左右子树的根结点：

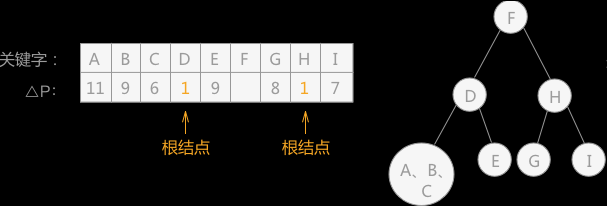
通过重新分别计算左右两查找子表的 △P 的值，得知左子树的根结点为 D，右子树的根结点为 H （如上图右侧所示），以两结点为分界线，继续判断两根结点的左右子树：

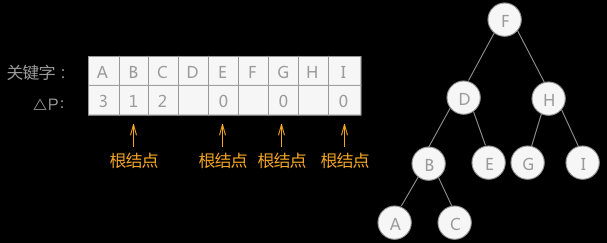
通过计算，构建的次优查找树如上图右侧二叉树所示。

后边还有一步，判断关键字 A 和 C 在树中的位置，最后一步两个关键字的权值为 0 ，分别作为结点 B 的左孩子和右孩子，这里不再用图表示。

注意：在建立次优查找树的过程中，由于只根据的各关键字的 P 的值进行构建，没有考虑单个关键字的相应权值的大小，有时会出现根结点的权值比孩子结点的权值还小，此时就需要适当调整两者的位置。

4.3. 总结

由于使用次优查找树和最优查找树的性能差距很小，构造次优查找树的算法的时间复杂度为 O(nlogn)，因此可以使用次优查找树表示概率不等的查找表对应的静态查找表（又称为静态树表）。

5. 动态查找表：二叉排序树（二叉查找树）

博客园: 二叉排序树（二叉查找树）

前几节介绍的都是有关静态查找表的相关知识，从本节开始介绍另外一种查找表——动态查找表。

动态查找表中做查找操作时，若查找成功可以对其进行删除；如果查找失败，即表中无该关键字，可以将该关键字插入到表中。

动态查找表的表示方式有多种，本节介绍一种使用树结构表示动态查找表的实现方法——二叉排序树（又称为“二叉查找树”）。

5.1. 什么是二叉排序树？

二叉排序树要么是空二叉树，要么具有如下特点：

• 二叉排序树中，如果其根结点有左子树，那么左子树上所有结点的值都小于根结点的值；
• 二叉排序树中，如果其根结点有右子树，那么右子树上所有结点的值都大小根结点的值；
• 二叉排序树的左右子树也要求都是二叉排序树；

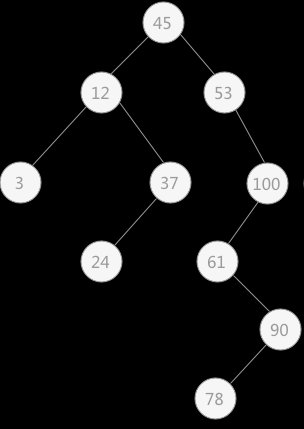
5.2. 使用二叉排序树查找关键字

5.3. 二叉排序树中插入关键字

二叉排序树本身是动态查找表的一种表示形式，有时会在查找过程中插入或者删除表中元素，当因为查找失败而需要插入数据元素时，该数据元素的插入位置一定位于二叉排序树的叶子结点，并且一定是查找失败时访问的最后一个结点的左孩子或者右孩子。

例如，在图 1 的二叉排序树中做查找关键字 1 的操作，当查找到关键字 3 所在的叶子结点时，判断出表中没有该关键字，此时关键字 1 的插入位置为关键字 3 的左孩子。

所以，二叉排序树表示动态查找表做插入操作，只需要稍微更改一下前面“查找关键字”的代码就可以实现。

5.4. 二叉排序树中删除关键字

在查找过程中，如果在使用二叉排序树表示的动态查找表中删除某个数据元素时，需要在成功删除该结点的同时，依旧使这棵树为二叉排序树。

假设要删除的为结点 p，则对于二叉排序树来说，需要根据结点 p 所在不同的位置作不同的操作，有以下 3 种可能：

1. 结点 p 为叶子结点，此时只需要删除该结点，并修改其双亲结点的指针即可；

2. 结点 p 只有左子树或者只有右子树，此时只需要将其左子树或者右子树直接变为结点 p 双亲结点的左子树即可；

3. 结点 p 左右子树都有，此时有两种处理方式：

   1. 令结点 p 的左子树为其双亲结点的左子树；结点 p 的右子树为其自身直接前驱结点的右子树

      

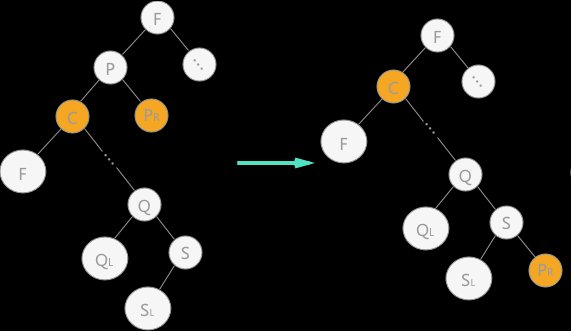
   2. 用结点 p 的直接前驱（或直接后继）来代替结点 p，同时在二叉排序树中对其直接前驱（或直接后继）做删除操作。如图 4 为使用直接前驱代替结点 p

      

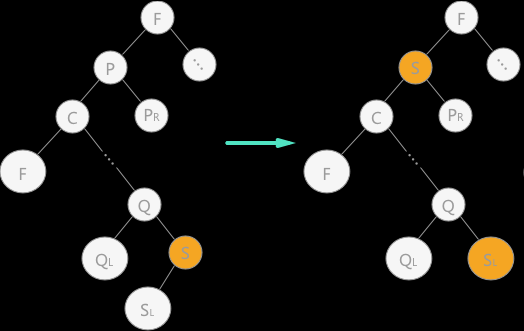
5.5. 总结

使用二叉排序树在查找表中做查找操作的时间复杂度同建立的二叉树本身的结构有关。即使查找表中各数据元素完全相同，但是不同的排列顺序，构建出的二叉排序树大不相同。

例如：查找表 {45，24，53，12，37，93} 和表 {12，24，37，45，53，93} 各自构建的二叉排序树图下图所示：

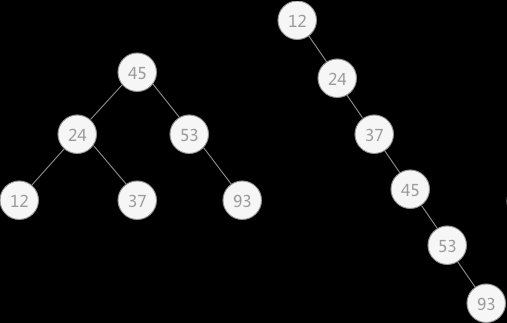
使用二叉排序树实现动态查找操作的过程，实际上就是从二叉排序树的根结点到查找元素结点的过程，所以时间复杂度同被查找元素所在的树的深度（层次数）有关。

为了弥补二叉排序树构造时产生如上图右侧所示的影响算法效率的因素，需要对二叉排序树做“平衡化”处理，使其成为一棵平衡二叉树。

平衡二叉树是动态查找表的另一种实现方式，下一节做重点介绍。