A.Hard Problem
题目大意:给你一个数n,然后让你计算一个子集大小,这个大小的子集要保证一定存在一个数是另一个数的约数,求出这个最小的数。
做法:显然后面的\(\frac{n}{2}\)个数是互相不为约数的。然后细节再随便搞一搞就行,可以发现\(ans=\lceil\frac{n}{2}\rceil+1\)。
#include<bits/stdc++.h>
using namespace std;
int n,t;
int main(){
scanf("%d",&t);
for(int i=1;i<=t;i++){
scanf("%d",&n);
printf("%d\n",(n+1)/2+1);
}
return 0;
}
B. Chessboard
题目大意:给你棋盘的大小n,m。你需要求出有多少种遍历方式可以遍历整个棋盘,但是在遍历过程中有限制:你不能让你涂完色的格子与其他涂完色的格子在涂色的格子上的最短距离变得更短。
做法:(以下直接抄的别人blog)
首先,我们可以观察到如下几个不难证明的性质:
- 两个被染上颜色的格子之间的距离始终为:曼哈顿距离。
- 一个染色方案是合法的,当且仅当:任何时刻,每行/列被染色的格子要么不存在,要么是连续的一段。
- 如果当前被染色的区域是个矩形,那么最后一个被染色的点,一定在角上。
如果当前被染色的区域是个\(r(r>=2)\)行\(c(c>=2)\)列的矩形,那么接下来要么扩充成 r+1 行 c 列的矩阵(扩充行),要么扩充成 r 行 c+1 列的矩形(扩充列)。并且根据当前状态中最后一个被染色的格子在哪个角上,扩充行/列的方案都是唯一的。
从 1∗1 的矩阵,到 n∗m 的矩阵,一共要扩充 n+m−2 次,其中有 n−1 次是扩充行,这样的决策有 \(C_{n+m-2}^{n-1}\) 种,又由于 1*1 时候的矩阵可以视为左上/右上/左下/右下角,答案需要乘以4.
所以最终答案为\(4C_{n+m-2}^{n-1}\)
具体做法只需要预处理阶乘,然后直接套组合数原始公式+用快速幂求逆即可。
小心\(n=1\)和\(m=1\)的情况。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define IL inline
typedef long long LL;
const int N = 2e6 + 3;
const LL mod = 1e9 + 7;
LL jc[N];
IL void init() {
jc[0] = 1;
for(int i=1;i<=2e6;i++) {
jc[i] = jc[i-1]*i%mod;
}
}
IL LL ksm(LL a,LL b,LL p) {
LL res = 1LL;
while(b) {
if(b&1LL) res = res * a % p;
a = a * a % p;
b >>= 1LL;
}
return res;
}
IL LL C(LL n,LL m,LL p) {
if(n < m) return 0;
return jc[n]*ksm(jc[m],p-2,p)%p*ksm(jc[n-m],p-2,p) % p;
}
int main() {
init();
int T; scanf("%d",&T);
while(T--) {
LL n,m; scanf("%lld%lld",&n,&m);
if(n == 1) {
if(m == 1) printf("1\n");
else printf("2\n");
continue;
}
if(m == 1) {
if(n == 1) printf("1\n");
else printf("2\n");
continue;
}
printf("%lld\n",4LL*C(n+m-2,n-1,mod)%mod);
}
return 0;
}
C. Digital Path
题目大意:你需要找出单调递增1且长度不小于4的路径有多少条。
做法:队友做的。我觉得就是个大模拟Orz。
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
const int MOD = 1e9 + 7;
const int addx[] = {-1, 0, 1, 0};
const int addy[] = {0, 1, 0, -1};
int a[N][N];
int f[N][N][4];
struct Point {
int x, y, a;
}P[1000005];
bool cmp(Point A, Point B) {
return A.a < B.a;
}
int main() {
//freopen("1.txt", "r", stdin);
int n, m;
scanf("%d%d", &n, &m);
int t = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
scanf("%d", &a[i][j]);
P[++t] = (Point) {i, j, a[i][j]};
}
sort(P + 1, P + t + 1, cmp);
for (int i = 1; i <= t; i++) {
int x = P[i].x, y = P[i].y;
for (int j = 0; j < 4; j++) {//四个方向
int fx = x + addx[j], fy = y + addy[j];
if (fx >= 1 && fx <= n && fy >= 1 && fy <= m && a[fx][fy] + 1 == a[x][y]) {
for (int k = 1; k < 4; k++) {
f[x][y][k] = (f[x][y][k] + f[fx][fy][k - 1]) % MOD;
}
f[x][y][3] = (f[x][y][3] + f[fx][fy][3]) % MOD;
}
}
if (f[x][y][1] == 0 && f[x][y][2] == 0 && f[x][y][3] == 0)
f[x][y][0] = 1;
}
int ans = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
int pd = 1;
for (int k = 0; k < 4; k++) {
int x = i + addx[k], y = j + addy[k];
if (x >= 1 && x <= n && y >= 1 && y <= m && a[x][y] == a[i][j] + 1) pd = 0;
}
if (pd)
ans = (ans + f[i][j][3]) % MOD;
}
printf("%d", ans);
return 0;
}
H.Prince and Princess
大意:王子要找到公主在哪个房间。有三类人,说真话的(包括公主),不说真话的,随便人。给你这三种人各自的人数a,b,c,你需要判断你最少需要问多少人才能问出来公主在哪个房间。
做法:显然当\(a>b+c\)时你就能问出来公主在哪,问的次数也显然是\(2(b+c)+1\),不过要小心\(1,0,0\)的情况应该输出0.
#include <bits/stdc++.h>
using namespace std;
int main() {
int a, b, c;
cin >> a >> b >> c;
if (a > b + c) {
if (a == 1 && b == 0 && c == 0)
printf("YES\n0");
else
printf("YES\n%d", (b + c) * 2 + 1);
}
else
printf("NO\n");
return 0;
}
J. Spy
大意:你需要给你的人配对,两人配成一对击败对面的队伍获得一定的名声值,你要求出最大的期望名声*n。
做法:假如此时你已经把所有人都配对好了,设此时你每个队队伍的力量值为\(d_i\),那么最后答案为$$ans=\sum_{i=1}n\sum_{j=1}n[d_i<a_j]p_j$$
我们可以发现配对的过程是一个二分图最大权匹配。边权就是\(b_i\)与\(c_j\)相连对答案的贡献$$\sum_{k=1}^n[b_i+c_j>a_k]p_k$$
然后这个题把(在我已知范围内的)除了bfs的\(O(n^3)\)以外的所有算法都给卡了。包括我写dfs的\(O(n^3)\)算法也过不去,甚至dfs的\(O(n^4)\)算法比\(O(n^3)\)还快。
这个板子需要记录一下,因为我不会写。
bfs ac。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define IL inline
typedef long long LL;
const int N = 400 + 3;
const int INF = 0x3f3f3f3f;
struct Kuhn_Munkers {
int n;
int W[N][N];
int Lx[N],Ly[N];
int left[N];
int slack[N];
int pre[N];
bool T[N];
IL void init(int n) {
this->n = n;
for(int i=1;i<=n;i++) fill(W[i],W[i]+1+n,INF);
}
IL void bfs(int u) {
fill(slack,slack+1+n,INF);
fill(pre,pre+1+n,0);
int x,y=0,yy=0,a;
left[y] = u;
for(;;) {
x = left[y]; a = INF, T[y] = true;
for(int i=1;i<=n;i++) if(!T[i]){
if(slack[i] > Lx[x]+Ly[i]-W[x][i]) {
slack[i] = Lx[x] + Ly[i] - W[x][i];
pre[i] = y;
}
if(slack[i] < a) a = slack[i],yy = i;
}
for(int i=0;i<=n;i++) {
if(T[i]) { Lx[left[i]] -= a; Ly[i] += a;}
else slack[i] -= a;
}
y = yy;
if(!left[y]) break;
}
while(y) left[y] = left[pre[y]], y = pre[y];
}
IL int KM() {
fill(Lx,Lx+1+n,0);
fill(Ly,Ly+1+n,0);
fill(left,left+1+n,0);
for(int i=1;i<=n;i++) {
fill(T,T+1+n,false);
bfs(i);
}
int ans = 0LL;
for(int j=1;j<=n;j++) ans += W[left[j]][j];
return ans;
}
}solver;
int n;
int p[N];
LL a[N],b[N],c[N];
int main() {
scanf("%d",&n); solver.init(n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&p[i]);
for(int i=1;i<=n;i++) scanf("%lld",&b[i]);
for(int i=1;i<=n;i++) scanf("%lld",&c[i]);
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
int v = 0;
for(int k=1;k<=n;k++) if(b[i]+c[j] > a[k]) v += p[k];
solver.W[i][j] = v;
}
}
printf("%d\n",solver.KM());
return 0;
}
dfs tle
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define IL inline
typedef long long LL;
const int N = 400 + 3;
const int INF = 0x3f3f3f3f;
struct Kuhn_Munkers {
int n;
int W[N][N];
int Lx[N],Ly[N];
int left[N];
int slack[N];
bool S[N],T[N];
IL void init(int n) {
this->n = n;
for(int i=1;i<=n;i++) fill(W[i],W[i]+1+n,INF);
fill(Lx,Lx+1+n,0);
fill(Ly,Ly+1+n,0);
fill(left,left+1+n,0);
}
bool match(int i) {
S[i] = true;
for(int j=1;j<=n;j++) if(!T[j]) {
if(Lx[i]+Ly[j] == W[i][j]) {
T[j] = true;
if(!left[j] || match(left[j])) {
left[j] = i;
return true;
}
}
else slack[j] = min(slack[j],Lx[i]+Ly[j]-W[i][j]);
}
return false;
}
IL void update() {
int a = INF;
for(int j=1;j<=n;j++) if(!T[j]) a = min(a,slack[j]);
for(int i=1;i<=n;i++) {
if(S[i]) Lx[i] -= a;
if(T[i]) Ly[i] += a;
else slack[i] -= a;
}
}
IL int KM() {
for(int i=1;i<=n;i++) {
left[i] = Lx[i] = Ly[i] = 0;
for(int j=1;j<=n;j++)
Lx[i] = max(Lx[i],W[i][j]);
}
for(int i=1;i<=n;i++) {
fill(slack,slack+1+n,INF);
for(;;) {
for(int j=1;j<=n;j++) S[j]=T[j]=0;
if(match(i)) break; else update();
}
}
int ans = 0LL;
for(int j=1;j<=n;j++) {
ans += W[left[j]][j];
}
return ans;
}
}solver;
int n;
int p[N];
LL a[N],b[N],c[N];
int main() {
scanf("%d",&n); solver.init(n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&p[i]);
for(int i=1;i<=n;i++) scanf("%lld",&b[i]);
for(int i=1;i<=n;i++) scanf("%lld",&c[i]);
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
int v = 0;
for(int k=1;k<=n;k++) if(b[i]+c[j] > a[k]) v += p[k];
solver.W[i][j] = v;
}
}
printf("%d\n",solver.KM());
return 0;
}
K.Triangle
大意:给你一个三角形,你需要找到一条线段平分这个三角形的面积,这个线段的一个端点已经给出了。
做法:简单的计算几何题,但是我写了3.5kb,非常难受。
给的端点如果不在三角形边上或者角上直接输出-1.
那么在三角形边上可以分成两种情况:
- 给的端点在角上。
- 给的端点在边上。
如果给的端点在角上,那么显然你只需要输出对边的中点即可。
如果给的端点在边上,那么你可以枚举这个端点相邻的两个角,然后利用正弦的面积公式,得出另一个端点在哪里,如果另一个端点不在三角形上就不要它。
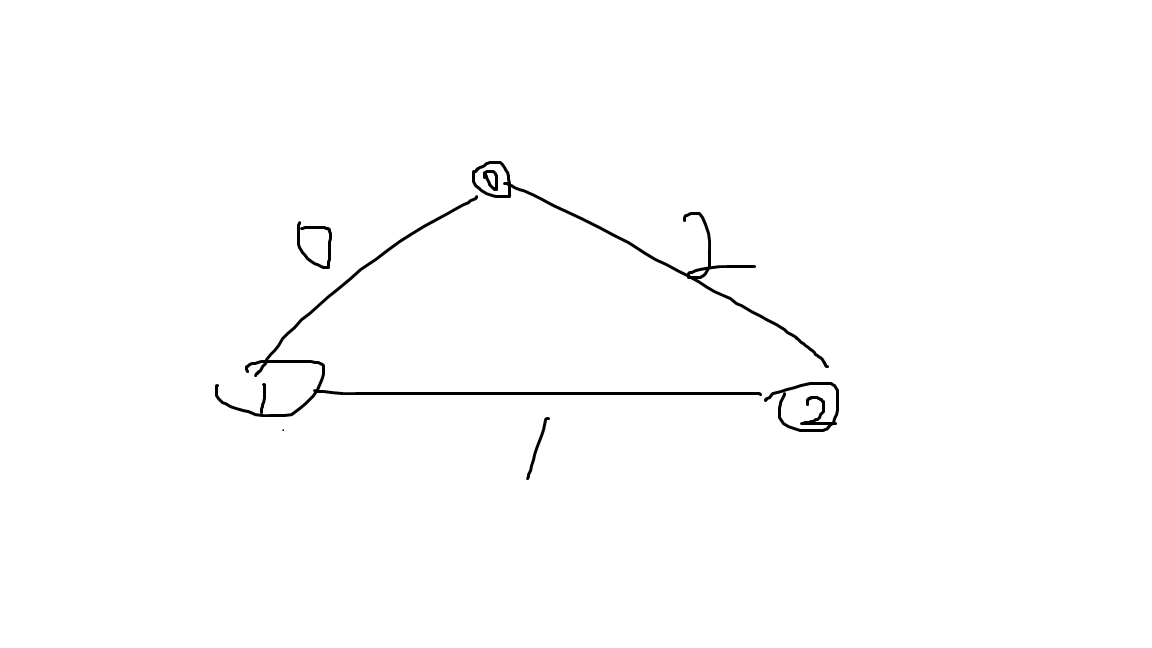
配一张图,看一下我的代码里边和角的命名。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<vector>
#include<algorithm>
using namespace std;
#define IL inline
typedef long long LL;
const double PI = acos(-1.0);
const double eps = 1e-10;
struct Point {
double x,y;
IL Point() {}
IL Point(double x,double y):x(x),y(y){}
};
typedef Point Vector;
IL Vector operator + (const Vector& A,const Vector& B) { return Vector(A.x+B.x,A.y+B.y);}
IL Vector operator - (const Vector& A,const Vector& B) { return Vector(A.x-B.x,A.y-B.y);}
IL Vector operator * (const Vector& A,double p) { return Vector(A.x*p,A.y*p);}
IL Vector operator / (const Vector& A,double p) { return Vector(A.x/p,A.y/p);}
IL bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y);}
IL int dcmp(double x) { if(fabs(x) < eps) return 0; else return x < 0 ? -1 : 1;}
IL bool operator == (const Point& A,const Point& B) { return dcmp(A.x-B.x) == 0 && dcmp(A.y-B.y) == 0;}
IL double Dot(const Vector& A,const Vector& B) { return A.x*B.x + A.y*B.y;}
IL double Length(const Vector& A) { return sqrt(Dot(A,A));}
IL double Angle(const Vector& A,const Vector& B) { return acos(Dot(A,B) / Length(A) / Length(B));}
IL double Cross(const Vector& A,const Vector& B) { return A.x*B.y - A.y*B.x;}
IL double Area2(const Point& A, const Point& B,const Point& C) { return Cross(B-A,C-A);}
IL Vector Rotate(const Vector& A,double rad) { return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));}
IL Vector Normal(const Vector& A) { double L = Length(A); return Vector(-A.y/L,-A.x/L);}
IL double DistanceToSegment(const Point& P,const Point& A,const Point& B) {
if(A == B) return Length(P-A);
Vector v1 = B-A, v2 = P-A, v3 = P-B;
if(dcmp(Dot(v1,v2)) < 0) return Length(v2);
else if(dcmp(Dot(v1,v3)) > 0) return Length(v3);
else return fabs(Cross(v1,v2)) / Length(v1);
}
int vtos[5][5];
int stov[5][5];
IL void init() {
vtos[0][1] = vtos[1][0] = 0;
vtos[0][2] = vtos[2][0] = 2;
vtos[1][2] = vtos[2][1] = 1;
stov[0][0] = 0; stov[0][1] = 1;
stov[1][0] = 1; stov[1][1] = 2;
stov[2][0] = 0; stov[2][1] = 2;
}
bool may[5];
IL int valid(Point* p) {
may[0]=may[1]=may[2] = false;
for(int i=0;i<3;i++) if(p[i] == p[3]) {
may[(i+1)%3] = true; return 1;
}
for(int i=0;i<3;i++) {
for(int j=0;j<i;j++) {
if(DistanceToSegment(p[3],p[i],p[j]) == 0) {
may[0]=may[1]=may[2] = true;
may[vtos[i][j]] = false;
return 2;
}
}
}
return 0;
}
IL void EndPoint_On_Vertices(Point* p) {
int now;
for(int i=0;i<3;i++) if(may[i]) now = i;
Point a = p[stov[now][0]] , b = p[stov[now][1]];
Point ans = a + (b-a) / 2.0;
printf("%lf %lf\n",ans.x,ans.y);
}
IL void EndPoint_On_Sides(Point *p) {
int pos;
for(int i=0;i<3;i++) if(!may[i]){ pos = i;}
for(int i=0;i<2;i++) {
int v1 = stov[pos][i], v2 = stov[pos][i^1], v3 = 3-v1-v2;
double S = Length(p[v2]-p[v1]) / 2.0 *Length(p[v3]-p[v1]);
double d = S / Length(p[3]-p[v1]);
Point ans = p[v1] + (p[v3]-p[v1]) / Length(p[v3]-p[v1]) * d;
if(DistanceToSegment(ans,p[v1],p[v3]) > eps) continue;
printf("%lf %lf\n",ans.x,ans.y); return;
}
printf("-1\n");
}
Point p[10];
int main() {
int T; scanf("%d",&T); init();
while(T--) {
for(int i=0;i<4;i++) {
int x,y; scanf("%d%d",&x,&y);
p[i] = Point(x,y);
}
int d = valid(p);
if(!d) { printf("-1\n"); continue;}
else if(d == 1) EndPoint_On_Vertices(p);
else EndPoint_On_Sides(p);
}
return 0;
}
后面随便复制粘贴一些别人博客我没写的题解。
