F Infinite String Comparision
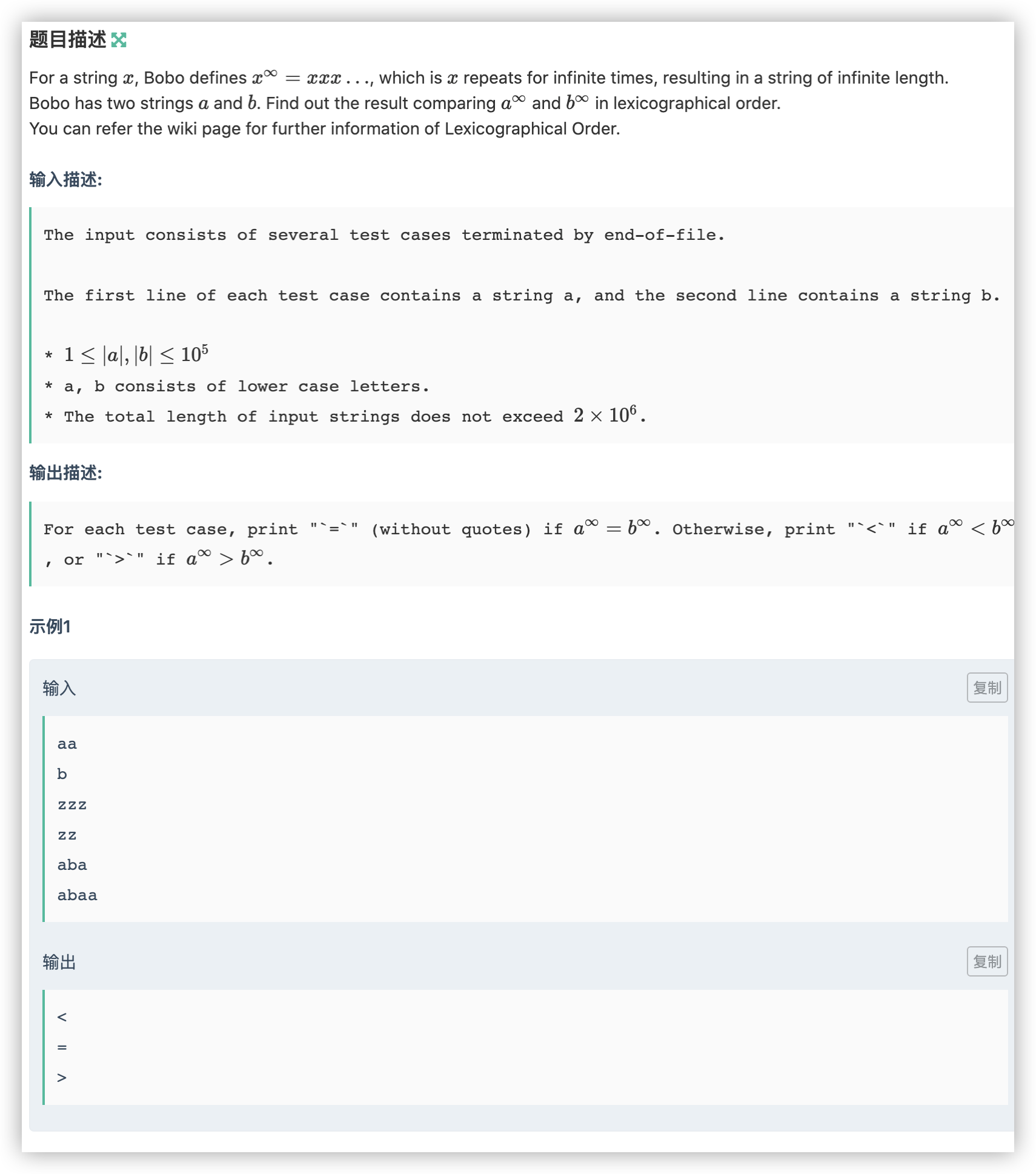
-
签到题,就是给你两个字符串,每个字符串可以以他本身为循环节循环无限次,让你以字典序规则判断两个字符串的大小。做法有不少,我就直接将字符串变为自己两倍,然后一次遍历判断每个位置对应的字符大小。
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <list>
#include <map>
#include <string>
#include <stack>
#include <math.h>
#include <stdlib.h>
#include <time.h>
#define S(X) scanf("%d",&(X))
#define SS(X, Y) scanf("%d%d",&(X),&(Y))
#define SSS(X,Y,Z) scanf("%d%d%d",&(X),&(Y),&(Z))
#define SL(X) scanf("%lld",&(X))
#define SLL(X, Y) scanf("%lld%lld",&(X),&(Y))
#define P(X) printf("%d\n",&(X))
#define P1 printf("-1\n")
using namespace std;
typedef double db;
typedef long long ll;
const int maxn=2e5+100;
using namespace std;
int main()
{
#ifdef ONLINE_JUDGE
#else
freopen(".vscode/in.txt","r",stdin);
#endif
string s,ss;
while(cin>>s>>ss)
{
s+=s;ss+=ss;
int lens=s.length();
int lenss=ss.length();
int len=max(lens,lenss);
bool flag=false;
char ans;
for(int i=0,s1=0,s2=0;i<=len+10;i++)
{
if(s[s1]<ss[s2]){
ans='<';
flag=true;break;
}
else if(s[s1]>ss[s2]){
ans='>';
flag=true;break;
}
s1++;s2++;
if(s1==lens)s1=0;
if(s2==lenss)s2=0;
}
if(flag)
printf("%c\n",ans);
else
printf("=\n");
}
return 0;
}
J Easy Integration
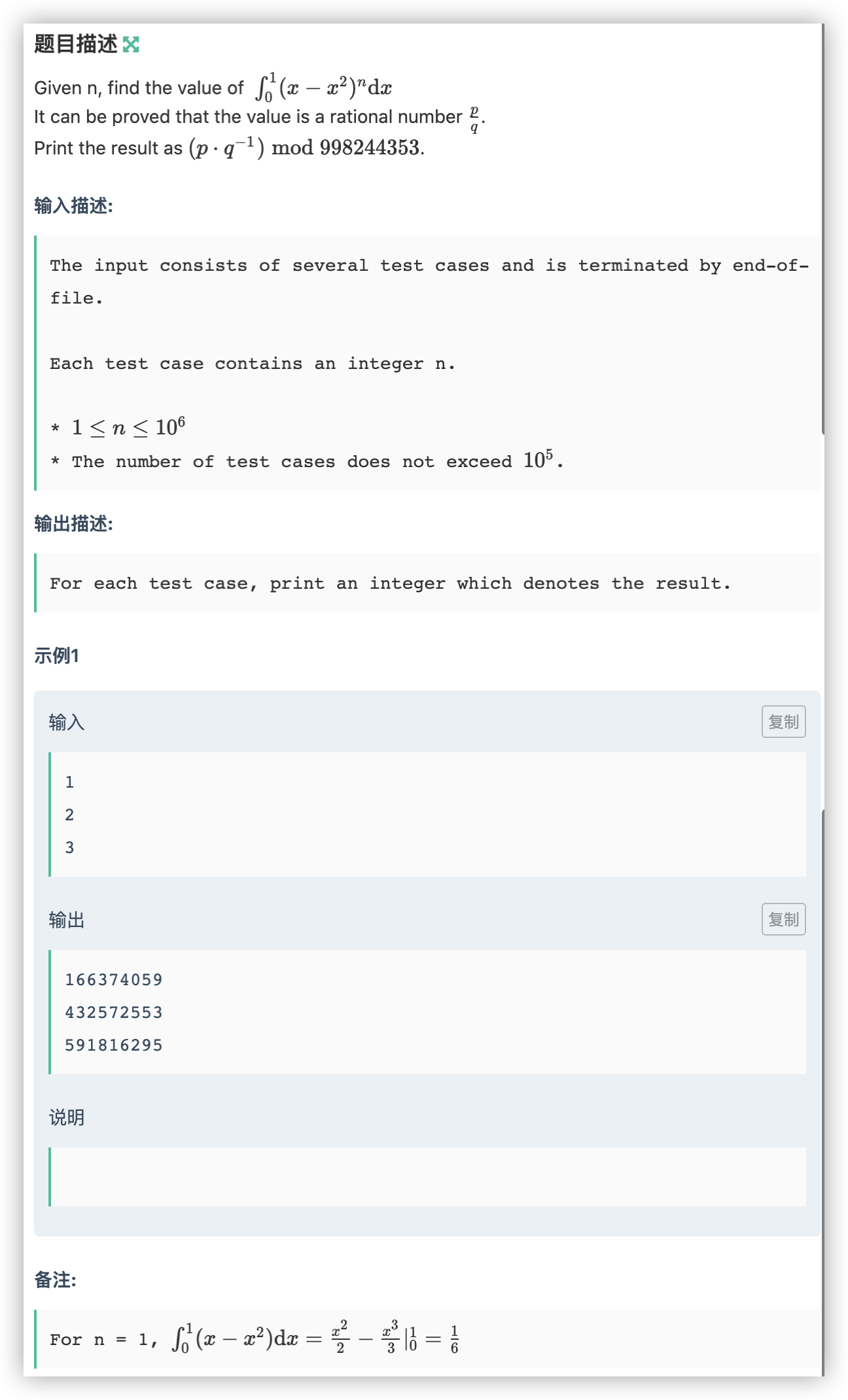
-
算出前几个例子的公式就能大致推出,如
\[1:1/(2*3)=1/6
\]
\[2: (1*2)/(3*4*5)=1/30
\]
\[3: (1*2*3)/(4*5*6*7)=1/140
\]
\[n: (1*2*3*...*n)*(1*2*3*...*n)/(1*2*3*...*n)*(1*2*3*...*2*n+1)=(n!)^2/(2*n+1)!
\]
由于答案取模,所以可以用数组存入2*n+1的阶乘,算好分子分母后求出这个分数%mod的值,
由于直接模会超精度,因此用到逆元算\((a/b)\%p\),即利用\(b^{mod-2}\)来算出b的逆元,
那么结果就是
\[((n!)^2/(2n+1)!)\%mod --> ((a\%mod)*((b^{mod-2}\%mod))\%mod
\]
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <list>
#include <map>
#include <string>
#include <stack>
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <iomanip>
#include<limits.h>
#define S(X) scanf("%d",&(X))
#define SS(X, Y) scanf("%d%d",&(X),&(Y))
#define SSS(X,Y,Z) scanf("%d%d%d",&(X),&(Y),&(Z))
#define SL(X) scanf("%lld",&(X))
#define SLL(X, Y) scanf("%lld%lld",&(X),&(Y))
using namespace std;
typedef double db;
typedef long long ll;
const int mod = 998244353;
const int maxn=2e6+1000;
ll quick(ll a,ll b)//快速幂用来求b^(mod-2)即b的逆元
{
ll ans=1;
while(b>0)
{
if(b&1)
ans=(ans*a)%mod;
b>>=1;
a=(a*a)%mod;
}
return ans;
}
ll F[maxn];
int main()
{
#ifdef ONLINE_JUDGE
#else
freopen(".vscode/in.txt","r",stdin);
#endif
F[0]=1;
for(int i=1;i<=2000100;i++)
F[i]=(F[i-1]*i)%mod;//求阶乘
//Ni[1]=1;
// for(int i=2;i<=INT_MAX-2;i++)
// Ni[i]=(mod-mod/i)*Ni[mod%i]%mod;
int n;
while(~S(n))
{
ll fenz=(F[n]*F[n])%mod;//分子
ll fenm=F[n<<1|1];//分母
//cout<<fenz<<" "<<fenm<<" "<<Ni[fenm]<<endl;
ll cnt=(fenz*(quick(fenm,mod-2)%mod))%mod;//答案的值了:((n!)^2/(2*n+1)!)%mod
printf("%lld\n",cnt);
}
return 0;
}