桶排序

一、思想
一句话总结：划分多个范围相同的区间，每个子区间自排序，最后合并。

桶排序是计数排序的扩展版本，计数排序可以看成每个桶只存储相同元素，而桶排序每个桶存储一定范围的元素，通过映射函数，将待排序数组中的元素映射到各个对应的桶中，对每个桶中的元素进行排序，最后将非空桶中的元素逐个放入原序列中。

桶排序需要尽量保证元素分散均匀，否则当所有数据集中在同一个桶中时，桶排序失效。

二、图解过程

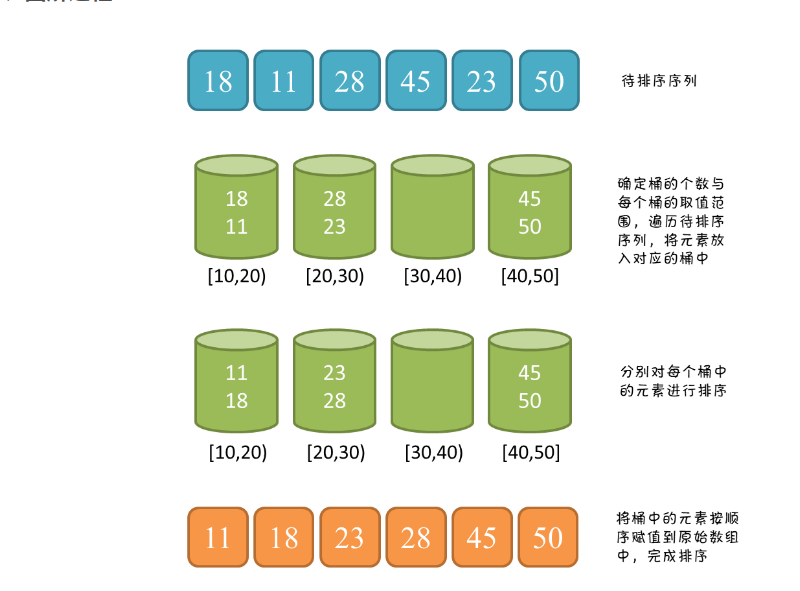
三、核心代码

public static void bucketSort(int[] arr){
    
    // 计算最大值与最小值
    int max = Integer.MIN_VALUE;
    int min = Integer.MAX_VALUE;
    for(int i = 0; i < arr.length; i++){
        max = Math.max(max, arr[i]);
        min = Math.min(min, arr[i]);
    }
    
    // 计算桶的数量
    int bucketNum = (max - min) / arr.length + 1;
    ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
    for(int i = 0; i < bucketNum; i++){
        bucketArr.add(new ArrayList<Integer>());
    }
    
    // 将每个元素放入桶
    for(int i = 0; i < arr.length; i++){
        int num = (arr[i] - min) / (arr.length);
        bucketArr.get(num).add(arr[i]);
    }
    
    // 对每个桶进行排序
    for(int i = 0; i < bucketArr.size(); i++){
        Collections.sort(bucketArr.get(i));
    }
    
    // 将桶中的元素赋值到原序列
	int index = 0;
	for(int i = 0; i < bucketArr.size(); i++){
		for(int j = 0; j < bucketArr.get(i).size(); j++){
			arr[index++] = bucketArr.get(i).get(j);
		}
	}  
}

　　

四、复杂度分析
1. 时间复杂度：O(N + C)
对于待排序序列大小为 N，共分为 M 个桶，主要步骤有：

N 次循环，将每个元素装入对应的桶中
M 次循环，对每个桶中的数据进行排序（平均每个桶有 N/M 个元素）
一般使用较为快速的排序算法，时间复杂度为 O ( N l o g N ) O(NlogN)O(NlogN)，实际的桶排序过程是以链表形式插入的。

整个桶排序的时间复杂度为：

O ( N ) + O ( M ∗ ( N / M ∗ l o g ( N / M ) ) ) = O ( N ∗ ( l o g ( N / M ) + 1 ) ) O(N)+O(M*(N/M*log(N/M)))=O(N*(log(N/M)+1))O(N)+O(M∗(N/M∗log(N/M)))=O(N∗(log(N/M)+1))

当 N = M 时，复杂度为 O ( N ) O(N)O(N)

2. 额外空间复杂度：O(N + M)
五、稳定性分析
桶排序的稳定性取决于桶内排序使用的算法。
————————————————
版权声明：本文为CSDN博主「str_818」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_27124771/article/details/87651495