算法分析作业(C|C++版本)

 

算法分析作业：

1. 使用快速排序和冒泡排序进行数组排序

2. 使用蛮力法进行字符串匹配

3. 实现大整数乘法

4. 实现循环赛制安排表

5. 运用减一算法，生成一个n个元素集合的幂集

6. 使用插人排序对序列2,6,1,4,5,3,2进行排序

7. 实现俄式乘法

8. 实现AVL树

9. 实现2-3树

10. 贪心算法实现活动安排

11. 贪心算法实现背包问题

1. 使用快速排序和冒泡排序进行数组排序

/*
 * @Author: bpf
 * @Date: 2020-04-01 08:54:13
 * @LastEditTime: 2020-04-01 10:12:08
 * @LastEditors: bpf
 * @Description: 使用快速和冒泡排序数组
 * @FilePath: Learn in the InternetCodeAlgorithmssortArray.cpp
 */
#include <stdio.h>

void Print(int a[], int n)
{
    for(int i=0; i<n; i++)
        printf("%d  ", a[i]);
}

void Switch(int *a, int *b)
{
    int tmp = 0;
    tmp = *a;
    *a = *b;
    *b = tmp;
}

void QuickSort(int a[], int n)
{
    int min = 0, tmp = 0;
    for(int i=0; i<n-1; i++)
    {
        min = i;
        for(int j=i+1; j<n; j++)
            if(a[min] > a[j])
                min = j;

        if(min != i)
            Switch(a+min, a+i);
    }    
}

void BubbleSort(int a[], int n)
{
    int tmp = 0;
    for(int i=0; i<=n-2; i++)
        for(int j=0; j<=n-2-i; j++)
            if(a[j] > a[j+1])
                Switch(a+j, a+j+1);
}

int main()
{
    int a [7] = {2, 6, 1, 4, 5, 3, 2};
    int Length = 7;
    printf("原数组：");
    Print(a, Length);
    printf("
快速排序法：");
    QuickSort(a, Length);
    Print(a, Length);
    printf("
冒泡排序法：");
    BubbleSort(a, Length);
    Print(a, Length);
    return 0;
}

/****** 快速排序
1. 获得源数组a
2. 输出源数组a
3. min = 0, 表示默认第一个元素为最小
4. i = 0, j = i+1
5. 第i轮排序, 从第j个元素开始, 与第min个元素比较
    如果a[min] > a[j], 则 min = j
    如果a[min] < a[j], 则跳过
6. j++ 直到 j == n
7. i++
8. 循环执行第5、6、7步，直到i == n-2
9. 输出排序后数组a

******* 冒泡排序
1. 获得源数组a
2. 输出源数组a
3. i = 0, j = 0
4. 第i轮排序, 从第j个元素开始, 与第j+1个元素比较
    如果a[j] > a[j+1], 则交换两个数
    如果a[j] < a[j+1], 则跳过
5. j++ 直到 j == n-2-i
6. i++
7. 循环执行第4、5、6步，直到i == n-2
8. 输出排序后数组a
*/

2. 使用蛮力法进行字符串匹配

/*
 * @Author: bpf
 * @Date: 2020-04-01 09:21:35
 * @LastEditTime: 2020-04-01 09:47:06
 * @LastEditors: bpf
 * @Description: 使用蛮力法进行字符串匹配
 * @FilePath: Learn in the InternetCodeAlgorithmscatchString.cpp
 */
#include <stdio.h>

int catStr(char s[], char cmp[])
{
    int i = 0, j = 0;
    for(i=0; s[i]!=''; i++)
    {
        for(j=0; cmp[j]!=''; j++)
        {
            if(s[i] !=cmp [j])
                break;
            else
                i++;
        }
        if(cmp[j] == '')
            return true;
    }
    return false;
}

int main()
{
    char s[100] = "I like apples and pears.";
    char cmp[16] = {""};
    printf("源字符串：%s
", s);
    printf("请输入匹配的字符串:");
    scanf("%s", cmp);
    if(catStr(s, cmp))
        printf("Yes");
    else
        printf("No");
}

/* 字符串匹配
1. 获得源字符串s
2. 输入匹配的字符串cmp
3. i = 0, j = 0
4. 判断字符串s与字符串cmp的第i个字符
    如果不同则移到字符串s的下一个字符, 即i++
    如果相同则再匹配cmp的第二个字符, 即j++
5. 重复第4步, 直到匹配完字符串s
6. 输出结果
*/

第1、2部分的 执行结果：

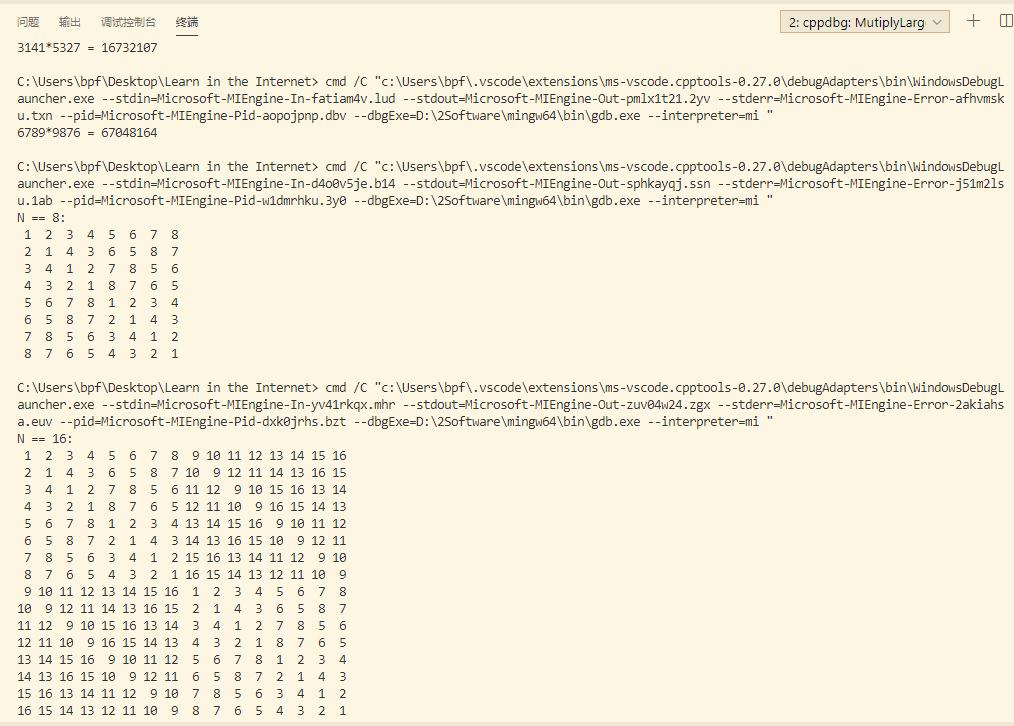
3. 实现大整数乘法

/*
 * @Author: bpf
 * @Description: 大整数乘法，此处数字使用十进制
 * @FilePath: Learn in the InternetCodeAlgorithmsMutiplyLarge.cpp
 */

#include <stdio.h>
#include <math.h>

/** 获取整数符号 */
int sign(int x) {
    if(x > 0)
        return 1;
    else if(x == 0)
        return 0;
    else
        return -1;
}

/** 大整数乘法运算 */
long int Mutiply(int x, int y, int n) {
    int s = sign(x) * sign(y);  // 符号
    x = abs(x);                 // 取绝对值
    y = abs(y);                 // 取绝对值

    if(n == 1) {
        if(x!=0 && y!=0)
            return s*x*y;
        else
            return 0;
    }
    else {
        int a = x / pow(10, n/2);       // a为x的左半边
        int b = x % int(pow(10, n/2));  // b为x的右半边
        int c = y / pow(10, n/2);       // c为y的左半边
        int d = y % int(pow(10, n/2));  // d为y的右半边

        int m1 = Mutiply(a, c, n/2);
        int m2 = Mutiply(a-b, d-c, n/2);
        int m3 = Mutiply(b, d, n/2);
        s = s * (m1*pow(10, n) + (m1+m2+m3)*pow(10, n/2) + m3);
        // printf("a=%d, b=%d, c=%d, d=%d, m1=%d, m2=%d, m3=%d, s=%d
", a,b,c,d,m1,m2,m3,s);

        return s;
    }
}

int main() {
    int x = 3141, y = 5327, n = 4;
    printf("%d*%d = %d", x, y, Mutiply(x, y, n));
}

4. 实现循环赛制安排表

/*
 * @Author: bpf
 * @Date: 2020-04-15 11:03:14
 * @LastEditTime: 2020-04-15 11:53:04
 * @Description: 循环赛安排
 * @FilePath: Learn in the InternetCodeAlgorithmsArrangment.cpp
 */
#include <stdio.h>
#define N 8

/** 输出数组 */
void printArray(int n, int a[][N]) {
    for(int i=0; i<n; i++) {
        for(int j=0; j<n; j++) {
            printf("%2d ", a[i][j]);
        }
        printf("
");
    }
}

void merger(int n, int a[][N]) {
    int m = n/2;
    for(int i=0; i<m; i++) {
        for(int j=0; j<m; j++) {
            a[i][j+m] = a[i][j] + m;
            a[i+m][j] = a[i][j+m];
            a[i+m][j+m] = a[i][j];
        }
    }
}

void arrangment(int n, int a[][N]) {
    if(n == 1) {
        a[0][0] = 1;
        return;
    }
    arrangment(n/2, a);
    merger(n, a);
}

int main() {
    int a[N][N] = {0};
    arrangment(N, a);
    printf("N == %d:
", N);
    printArray(N, a);
}

第3、4部分的 执行结果：

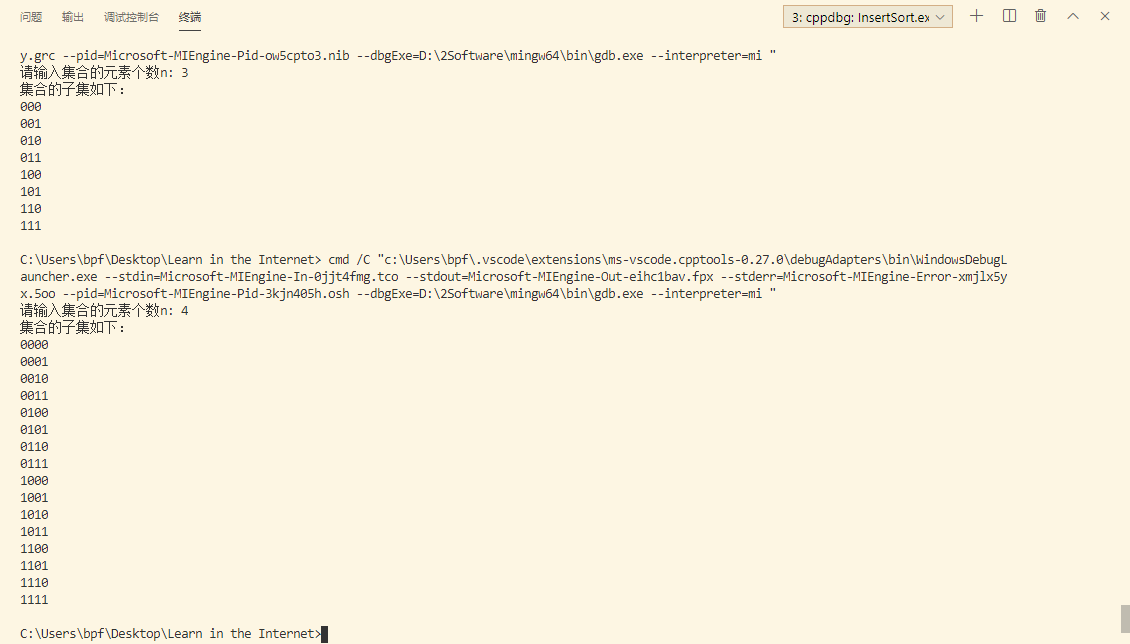
5. 运用减一算法，生成一个n个元素集合的幂集

/*
 * @Author: bpf
 * @Date: 2020-04-29 09:51:30
 * @LastEditTime: 2020-04-29 11:27:21
 * @Description: 集合的幂集, 使用0、1表示第i个元素是否存在, 如下所示
 *    000: 空集  |  001: a1  |  010: a2  |  110: a1,a2
 * @FilePath: Learn in the InternetCodeAlgorithmsSonSet.cpp
 */
#include <stdio.h>
#include <string.h>

void SonSet(int n) {
    short bit[1000][n];
    memset(bit, 0, sizeof(bit));    // 值置为0
    int sum = 1, count = 1;         // sum计算第i轮生成的子集个数,count计算总个数
    for(int i=n-1; i>=0; i--) {
        for(int j=0; j<sum; j++)
        {
            for(int k=0; k<n; k++)
                bit[sum+j][k] = bit[0+j][k];    // 赋值前sum个给后sum个
            bit[sum+j][i] = 1;
            count++;
        }
        sum *= 2;
    }
    
    for(int i=0; i<count; i++) {        // 输出幂集
        for(int j=0; j<n; j++) {
            printf("%d", bit[i][j]);
        }
        printf("
");
    }
}

int main() {
    int n = 0;
    printf("请输入集合的元素个数n: ");
    scanf("%d", &n);
    printf("集合的子集如下：
");
    SonSet(n);

    return 0;
}

6. 使用插人排序对序列2,6,1,4,5,3,2进行排序

/*
 * @Author: bpf
 * @Date: 2020-04-29 09:21:09
 * @LastEditTime: 2020-04-29 11:29:33
 * @Description: 插入排序
 * @FilePath: Learn in the InternetCodeAlgorithmsInsertSort.cpp
 */
#include <stdio.h>
// 插入排序
void InsertSort(int a[], int n) {
    int t = 0, j = 0;
    for(int i=1; i<n; i++) {
        t = a[i];
        for(j = i-1; j>=0 && a[j]>t; j--) {
            a[j+1] = a[j];
        }
        a[j+1] = t;
    }
}
//输出序列
void printArray(int a[], int n) {
    for(int i=0; i<n; i++) {
        printf("%d ", a[i]);
    }
    printf("
");
}

int main() {
    int a[7] = {2, 6, 1, 4, 5, 3, 2};
    printf("排序前：");
    printArray(a, 7);
    InsertSort(a, 7);
    printf("排序后：");
    printArray(a, 7);

    return 0;
}

7. 实现俄式乘法

/*
 * @Author: bpf
 * @Date: 2020-04-29 11:10:48
 * @LastEditTime: 2020-04-29 11:30:57
 * @Description: 俄氏乘法
 * @FilePath: Learn in the InternetCodeAlgorithmsEMutiply.cpp
 */
#include <stdio.h>

int EMutiply(int m, int n) {
    int sum = 0;
    while (m != 0)
    {
        if(m%2 != 0) {
            sum += n;
            m--;
        }
        else
        {
            m /= 2;
            n *= 2;
        }
    }
    
    return sum;
}

int main() {
    int m, n;
    printf("请输入两个整数(空格隔开)：");
    sacnf("%d %d", &m, &n);
    printf("%d x %d = %d
", EMutiply(m, n));
}

第6、7部分的执行结果：

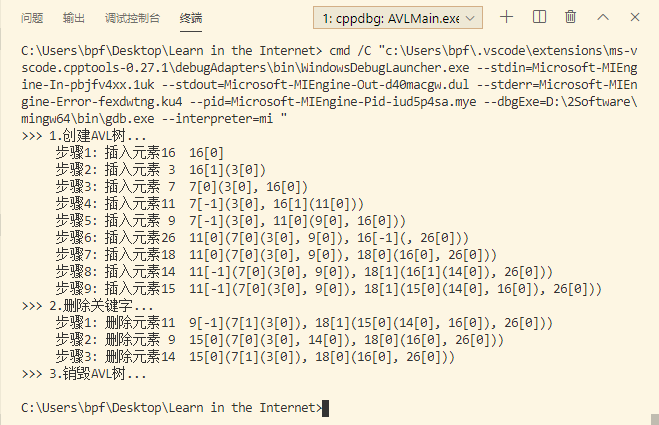
8. 实现AVL树

/*
 * @Author: bpf
 * @Date: 2020-05-13 08:37:26
 * @LastEditTime: 2020-05-13 14:15:00
 * @Description: 算法实现AVL树
 * @FilePath: Learn in the InternetCodeAlgorithmsavlTree.cpp
 */

#include <stdio.h>
#include <malloc.h>
typedef int KeyType;       // 关键字类型
typedef char InfoType;     // 数据类型
typedef struct note
{
    KeyType key;           // 关键字
    InfoType data;         // 数据域
    int bf;                   // 平衡因子
    struct note *lchild;
    struct note *rchild;
} BSTNode;

// 输出AVL树
void dispBSTree(BSTNode *b)
{
    if (b != NULL)
    {
        printf("%d[%d]", b->key, b->bf);
        if (b->lchild != NULL || b->rchild != NULL)
        {
            printf("(");
            dispBSTree(b->lchild);
            if (b->rchild != NULL)
                printf(", ");
            dispBSTree(b->rchild);
            printf(")");
        }
    }
}

// 插入元素时处理左子树
void leftProcess(BSTNode *&p, int &taller)
{
    BSTNode *p1, *p2;
    if (p->bf == 0)
    { // 原左右子树等高，现左子树高右子树1
        p->bf = 1;
        taller = 1;
    }
    else if (p->bf == -1)
    { // 原左子树低右子树1，现左右子树登高
        p->bf = 0;
        taller = 0;
    }
    else
    {
        p1 = p->lchild;
        if (p1->bf == 1)
        { // 新结点插入在结点b的左孩子的左子树上,要作LL调整
            p->lchild = p1->rchild;
            p1->rchild = p;
            p->bf = p1->bf = 0;
            p = p1;
        }
        else if (p1->bf == -1)
        { // 新结点插入在结点b的左孩子的右子树上,要作LR调整
            p2 = p1->rchild;
            p1->rchild = p2->lchild;
            p2->lchild = p1;
            p->lchild = p2->rchild;
            p2->rchild = p;
            if (p2->bf == 0) // 新结点插在p2处作为叶子结点的情况
                p->bf = p1->bf = 0;
            else if (p2->bf == 1)
            { // 新结点插在p2的左子树上的情况
                p1->bf = 0;
                p->bf = -1;
            }
            else
            { // 新结点插在p2的右子树上的情况
                p1->bf = 1;
                p->bf = 0;
            }
            p = p2;
            p->bf = 0; // 仍将p指向新的根结??,并置其bf值为0
        }
        taller = 0;
    }
}

// 插入元素时处理右子树
void rightProcess(BSTNode *&p, int &taller)
{
    BSTNode *p1, *p2;
    if (p->bf == 0)
    { // 原左右子树等高，现左子树低右子树1
        p->bf = -1;
        taller = 1;
    }
    else if (p->bf == 1)
    { // 原左子树高右子树1，现左右子树等高
        p->bf = 0;
        taller = 0;
    }
    else
    {
        p1 = p->rchild;
        if (p1->bf == -1)
        { // 新结点插入在结点b的右孩子的右子树上,要作RR调整
            p->rchild = p1->lchild;
            p1->lchild = p;
            p->bf = p1->bf = 0;
            p = p1;
        }
        else if (p1->bf == 1)
        { // 新结点插入在结点b的右孩子的左子树上,要作RL调整
            p2 = p1->lchild;
            p1->lchild = p2->rchild;
            p2->rchild = p1;
            p->rchild = p2->lchild;
            p2->lchild = p;
            if (p2->bf == 0) //新结点插在p2处作为叶子结点的情况
                p->bf = p1->bf = 0;
            else if (p2->bf == -1)
            { //新结点插在p2的右子树上的情况
                p1->bf = 0;
                p->bf = 1;
            }
            else
            { //新结点插在p2的左子树上的情况
                p1->bf = -1;
                p->bf = 0;
            }
            p = p2;
            p->bf = 0; //仍将p指向新的根结??,并置其bf值为0
        }
        taller = 0;
    }
}

// 插入元素
int insertElement(BSTNode *&b, KeyType e, int &taller)
{
    if (b == NULL)
    {
        b = (BSTNode *)malloc(sizeof(BSTNode));
        b->key = e;
        b->lchild = b->rchild = NULL;
        b->bf = 0;
        taller = 1;
    }
    else
    {
        if (e == b->key)
        { //树中已存在和e有相同关键字的结点则不再插入
            taller = 0;
            return 0;
        }
        if (e < b->key)
        {
            if ((insertElement(b->lchild, e, taller)) == 0)
                return 0;
            if (taller == 1) //已插入到结点b的左子树中且左子树长高
                leftProcess(b, taller);
        }
        else
        {
            if ((insertElement(b->rchild, e, taller)) == 0)
                return 0;
            if (taller == 1) //已插入到b的右子树且右子树长高
                rightProcess(b, taller);
        }
    }
    return 1;
}

// 删除元素时处理左子树
void leftProcessDelete(BSTNode *&p, int &taller) //在删除结点时进行左侧处理
{
    BSTNode *p1, *p2;
    if (p->bf == 1)
    {
        p->bf = 0;
        taller = 1;
    }
    else if (p->bf == 0)
    {
        p->bf = -1;
        taller = 0;
    }
    else
    {
        p1 = p->rchild;
        if (p1->bf == 0)
        { //需作RR调整
            p->rchild = p1->lchild;
            p1->lchild = p;
            p1->bf = 1;
            p->bf = -1;
            p = p1;
            taller = 0;
        }
        else if (p1->bf == -1)
        { //需作RL调整
            p->rchild = p1->lchild;
            p1->lchild = p;
            p->bf = p1->bf = 0;
            p = p1;
            taller = 1;
        }
        else
        { //需作RL调整
            p2 = p1->lchild;
            p1->lchild = p2->rchild;
            p2->rchild = p1;
            p->rchild = p2->lchild;
            p2->lchild = p;
            if (p2->bf == 0)
            {
                p->bf = 0;
                p1->bf = 0;
            }
            else if (p2->bf == -1)
            {
                p->bf = 1;
                p1->bf = 0;
            }
            else
            {
                p->bf = 0;
                p1->bf = -1;
            }
            p2->bf = 0;
            p = p2;
            taller = 1;
        }
    }
}

// 删除元素时处理右子树
void rightProcessDelete(BSTNode *&p, int &taller) //在删除结点时进行右侧处理
{
    BSTNode *p1, *p2;
    if (p->bf == -1)
    {
        p->bf = 0;
        taller = -1;
    }
    else if (p->bf == 0)
    {
        p->bf = 1;
        taller = 0;
    }
    else
    {
        p1 = p->lchild;
        if (p1->bf == 0)
        { //需作LL调整
            p->lchild = p1->rchild;
            p1->rchild = p;
            p1->bf = -1;
            p->bf = 1;
            p = p1;
            taller = 0;
        }
        else if (p1->bf == 1)
        { //需作RL调整
            p->lchild = p1->rchild;
            p1->rchild = p;
            p->bf = p1->bf = 0;
            p = p1;
            taller = 1;
        }
        else
        { //需作LR调整
            p2 = p1->rchild;
            p1->rchild = p2->lchild;
            p2->lchild = p1;
            p->lchild = p2->rchild;
            p2->rchild = p;
            if (p2->bf == 0)
            {
                p->bf = 0;
                p1->bf = 0;
            }
            else if (p2->bf == 1)
            {
                p->bf = -1;
                p1->bf = 0;
            }
            else
            {
                p->bf = 0;
                p1->bf = 1;
            }
            p2->bf = 0;
            p = p2;
            taller = 1;
        }
    }
}

// 处理被删除节点左右子树不空的情况
void deleteNotNull(BSTNode *q, BSTNode *&r, int &taller)
{
    if (r->rchild == NULL)
    {
        q->key = r->key;
        q = r;
        r = r->lchild;
        free(q);
        taller = 1;
    }
    else
    {
        deleteNotNull(q, r->rchild, taller);
        if (taller == 1)
            rightProcessDelete(r, taller);
    }
}

// 删除元素
int deleteElement(BSTNode *&p, KeyType x, int &taller)
{
    int k;
    BSTNode *q;
    if (p == NULL)
        return 0;
    else if (x < p->key)
    {
        k = deleteElement(p->lchild, x, taller);
        if (taller == 1)
            leftProcessDelete(p, taller);
        return k;
    }
    else if (x > p->key)
    {
        k = deleteElement(p->rchild, x, taller);
        if (taller == 1)
            rightProcessDelete(p, taller);
        return k;
    }
    else
    {
        q = p;
        if (p->rchild == NULL)
        { // 被删结点右子树为空
            p = p->lchild;
            free(q);
            taller = 1;
        }
        else if (p->lchild == NULL)
        { // 被删结点左子树为空
            p = p->rchild;
            free(q);
            taller = 1;
        }
        else
        { // 被删结点左右子树均不空
            deleteNotNull(q, q->lchild, taller);
            if (taller == 1)
                leftProcessDelete(q, taller);
            p = q;
        }
        return 1;
    }
}

// 销毁AVL树
void destroyBSTree(BSTNode *&b)
{
    if (b != NULL)
    {
        destroyBSTree(b->lchild);
        destroyBSTree(b->rchild);
        free(b);
    }
}

主函数：

/*
 * @Author: bpf
 * @Date: 2020-05-13 10:49:57
 * @LastEditTime: 2020-05-13 13:47:11
 * @Description: AVL测试
 * @FilePath: Learn in the InternetCodeAlgorithmsAVLMain.cpp
 */

# include <stdio.h>
# include "avlTree.cpp"

int main() {
    BSTNode *b = NULL;
    KeyType a[] = {16, 3, 7, 11, 9, 26, 18, 14, 15};
    int n = 9;
    int taller = 0;
    printf(">>> 1.创建AVL树...
");
    for(int i=0; i<n; i++) {
        printf("     步骤%d: 插入元素%2d  ", i+1, a[i]);
        insertElement(b, a[i], taller);
        dispBSTree(b);
        printf("
");
    }

    printf(">>> 2.删除关键字...
");
    int e[] = {11, 9, 14};
    for(int i=0; i<3; i++) {
        printf("     步骤%d: 删除元素%2d  ", i+1, e[i]);
        deleteElement(b, e[i], taller);
        dispBSTree(b);
        printf("
");
    }
    
    printf(">>> 3.销毁AVL树...
");
    destroyBSTree(b);

    return 0;
}

9. 实现2-3树

　　此算法中删除元素方法还不够完善。

/*
 * @Author: bpf
 * @Date: 2020-05-13 14:11:00
 * @LastEditTime: 2020-05-13 20:45:45
 * @Description: 实现2-3树
 * @FilePath: Learn in the InternetCodeAlgorithmsB3Tree.cpp
 */

#include <stdio.h>
#include <malloc.h>
#include <memory.h>
#define NUM(p)  ((p==NULL)? 0 : p->num)

typedef struct node {
    int a[3];   
    int num;    // 存储数组长度1,2,3

    struct node *left_child;
    struct node *mid_child;
    struct node *right_child;
    struct node *tmp_child;

    struct node *parent;
} Btree, *BtreePtr;

void exchange(int *a, int *b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

// 创建节点
BtreePtr _node(const int key) {
    BtreePtr p = (BtreePtr)malloc(sizeof(Btree));
    if (p != NULL) {
        memset(p, 0, sizeof(p));
        p->a[0] = key;
        p->num = 1;
        p->left_child = NULL;
        p->right_child = NULL;
        p->mid_child = NULL;
        p->tmp_child = NULL;
        p->parent = NULL;
    }
    else {
        puts("内存不足");
    }
    return p;
}

// 排序数组
void _sort(BtreePtr b) {
    int length = b->num;
    for (int i = 0; i < length; i++) {
        for (int j = i; j < length; j++) {
            if ((b->a[j]) < (b->a[i])) {
                exchange(&(b->a[j]), &(b->a[i]));
            }
        }
    }
}

// 平衡2-3树
BtreePtr _checkNum(BtreePtr p) {
    if (NUM(p) == 1) {  //2-结点
        if (NUM(p->left_child) == 3) {  //case 2
            p->a[1] = p->left_child->a[1];
            p->num++;
            _sort(p);

            BtreePtr l = _node(p->left_child->a[0]);
            l->left_child = p->left_child->left_child;
            l->parent = p;

            BtreePtr r = _node(p->left_child->a[2]);
            r->left_child = p->left_child->mid_child;
            r->right_child = p->left_child->right_child;
            r->parent = p;


            p->left_child = l;
            p->mid_child = r;
        }
        else if (NUM(p->right_child) == 3) {  //case 3
            p->a[1] = p->right_child->a[1];
            p->num++;
            _sort(p);

            BtreePtr l = _node(p->right_child->a[0]);
            l->left_child = p->right_child->left_child;
            l->parent = p;

            BtreePtr r = _node(p->right_child->a[2]);
            r->left_child = p->right_child->mid_child;
            r->right_child = p->right_child->right_child;
            r->parent = p;

            p->mid_child = l;
            p->right_child = r;
        }

    }
    else if (NUM(p) == 2) {  //3-结点
        if (NUM(p->left_child) == 3) {  //case 4
            p->a[2] = p->left_child->a[1];
            p->num++;
            _sort(p);

            p->tmp_child = p->mid_child;
            p->mid_child = _node(p->left_child->a[2]);

            BtreePtr l = _node(p->left_child->a[0]);
            l->left_child = p->left_child->left_child;
            l->right_child = p->left_child->mid_child;
            l->parent = p;

            BtreePtr r = _node(p->left_child->a[2]);
            r->left_child = p->left_child->tmp_child;
            r->right_child = p->left_child->right_child;
            r->parent = p;

            p->left_child = l;
        }
        else if (NUM(p->right_child) == 3) {  //case 5
            p->a[2] = p->right_child->a[1];
            p->num++;
            _sort(p);

            p->tmp_child = _node(p->right_child->a[2]); //

            BtreePtr l = _node(p->right_child->a[0]);
            l->right_child = p->right_child->left_child;
            l->right_child = p->right_child->mid_child;
            l->parent = p;

            BtreePtr r = _node(p->right_child->a[2]);
            r->right_child = p->right_child->tmp_child;
            r->right_child = p->right_child->right_child;
            r->parent = p;

            p->right_child = l;
        }
        else if (NUM(p->mid_child) == 3) {
            p->a[2] = p->mid_child->a[1];
            p->num++;
            _sort(p);

            //p->tmp_child = p->mid_child;
            //p->mid_child = _node(p->left_child->a[2]);

            BtreePtr l = _node(p->mid_child->a[0]);
            l->left_child = p->mid_child->left_child;
            l->right_child = p->mid_child->mid_child;
            l->parent = p;

            BtreePtr r = _node(p->mid_child->a[2]);
            r->left_child = p->mid_child->tmp_child;
            r->right_child = p->mid_child->right_child;
            r->parent = p;

            p->mid_child = l;
            p->tmp_child = r;
        }
    }
    if (p->num == 3) {
        if (p->parent == NULL) {  // case 1;
            BtreePtr t = p->left_child;
            p->left_child = _node(p->a[0]);
            p->left_child->left_child = t;
            p->left_child->right_child = p->mid_child;
            p->left_child->parent = p;

            t = p->right_child;
            p->right_child = _node(p->a[2]);
            p->right_child->left_child = p->tmp_child;
            p->right_child->right_child = t;
            p->right_child->parent = p;

            p->mid_child = NULL;
            p->tmp_child = NULL;

            p->a[0] = p->a[1];
            p->num = p->num - 2;
        }
    }
    return p;
}

// 插入元素子函数
BtreePtr _insertBTree(BtreePtr b, const int key, const int pos) {
    if (b->left_child == NULL && b->right_child == NULL) {  //叶子节点
        b->a[b->num] = key;
        b->num++;
        _sort(b);
    }
    else {
        if (b->num == 1) {
            if (key < b->a[0]) { //num =1, 2
                b->left_child = _insertBTree(b->left_child, key, pos);
            }
            else if (key > b->a[0]) { //num = 2
                b->right_child = _insertBTree(b->right_child, key, pos);
            }
        }
        else if (b->num == 2) {
            if (key < b->a[0]) { //num =1, 2
                b->left_child = _insertBTree(b->left_child, key, pos);
            }
            else if (key > b->a[1]) { //num = 2
                b->right_child = _insertBTree(b->right_child, key, pos);
            }
            else {
                b->mid_child = _insertBTree(b->mid_child, key, pos);
            }
        }
    }

    b = _checkNum(b);
    return b;
}

// 插入元素
BtreePtr insertBTree(BtreePtr root, const int key, const int pos) {
    if (root == NULL) {
        root = _node(key);
    }
    else {
        root = _insertBTree(root, key, pos);
    }
    return root;
}

// 处理删除节点数据项只有一个的情况
BtreePtr _deleteGen(BtreePtr b, const int key) {
    BtreePtr b1 = b->right_child;

    if(b1->num == 1 && (b1->left_child==NULL || b1->right_child==NULL)) {
        // b = insertBTree(b->left_child, b1->a[0], b->left_child->num+1); // 此方法不理想
        // b->num++;
        // b->left_child = b->right_child = NULL;
        // free(b1->parent);
        // free(b1);
        
        b1->left_child = b->left_child;
        free(b);
        b = b1;
    }
    else if(b1->num == 1 && (b1->left_child!=NULL || b1->right_child!=NULL)) {
        b->a[0] = b1->a[0];
        _deleteGen(b1, key);
    }
    else if(b1->num == 2) {
        b->a[0] = b1->a[0];
        b1->a[0] = b1->a[1];
        b1->num--;
    }
    // else if(b1->num == 2 && (b1->left_child!=NULL || b1->right_child!=NULL)) { // 包含在第三种情况中
    //     b->a[0] = b1->a[0];
    //     b1->a[0] = b1->a[1];
    //     b1->num--;
    // }

    return b;
}

// 处理删除元素子函数
BtreePtr _deleteBTree(BtreePtr b, const int key) {
    if (b->left_child == NULL && b->right_child == NULL) {  // 叶子节点
        switch (b->num) {
        case 1:
            if(b->a[0] == key);
            break;
        case 2:
            if(b->a[0] == key)
                b->a[0] = b->a[1];
            else if(b->a[1] == key);
            break;
        case 3:
            if(b->a[0] == key) {
                b->a[0] = b->a[1];
                b->a[1] = b->a[2];
            }
            else if(b->a[1] == key)
                b->a[1] = b->a[2];
            else if(b->a[2] == key);
            break;
        }
        if(b != NULL)
            b->num--;
        // _sort(b);
        _checkNum(b);
    }
    else {
        if (b->num == 1) {
            if (key < b->a[0]) { //num =1, 2
                b->left_child = _deleteBTree(b->left_child, key);
                if(b->left_child->num == 0)
                    b->left_child = NULL;
            }
            else if (key > b->a[0]) { //num = 2
                b->right_child = _deleteBTree(b->right_child, key);
                if(b->right_child->num == 0)
                    b->right_child = NULL;
            }
            else
                b = _deleteGen(b, key);
        }
        else if (b->num == 2) {
            if(key == b->a[0]) {
                b->a[0] = b->a[1];
                b->num--;
            }
            else if(key == b->a[1]) {
                b->num--;
            }
            else if (key < b->a[0]) { //num =1, 2
                b->left_child = _deleteBTree(b->left_child, key);
            }
            else if (key > b->a[1]) { //num = 2
                b->right_child = _deleteBTree(b->right_child, key);
            }
            else {
                b->mid_child = _deleteBTree(b->mid_child, key);
            }
        }
    }

    b = _checkNum(b);
    return b;
}

// 删除元素
BtreePtr deleteBTree(BtreePtr root, const int key) {
    if (root == NULL) {
        return root;
    }
    else {
        root = _deleteBTree(root, key);
    }
    return root;
}

// 输出2-3树
void dispTree(BtreePtr p) {
    if(p != NULL) {
        switch (NUM(p))
        {
        case 1:
            printf("[%d]", p->a[0]);
            break;
        case 2:
            printf("[%d,%d]", p->a[0], p->a[1]);
            break;
        case 3:
            printf("[%d,%d,%d]", p->a[0], p->a[1], p->a[2]);
            break;
        }
        if(p->left_child!= NULL || p->mid_child!= NULL || p->right_child!= NULL) {
            printf(" (");
            dispTree(p->left_child);
            if (p->mid_child != NULL)
                printf(", ");
            dispTree(p->mid_child);
            if(p->right_child != NULL)
                printf(", ");
            dispTree(p->right_child);
            printf(")");
        }
    }
}

// 销毁2-3树
void freeTree(BtreePtr p) {
    if (p->left_child != NULL) {
        freeTree(p->left_child);
    }
    if (p->right_child != NULL) {
        freeTree(p->right_child);
    }
    if (p->mid_child != NULL) {
        freeTree(p->mid_child);
    }
    free(p);
    p = NULL;
}

主函数：

/*
 * @Author: bpf
 * @Date: 2020-05-13 20:36:47
 * @LastEditTime: 2020-05-13 20:40:30
 * @Description: 测试2-3树
 * @FilePath: Learn in the InternetCodeAlgorithmsB3Main.cpp
 */
# include <stdio.h>
# include "B3Tree.cpp"

int main() {
    int a[] = {9, 5, 8, 3, 2, 4, 7};
    int n = 7;
    printf(">>> 1.创建2-3树...
");
    BtreePtr b = NULL;
    for (int i = 0; i < n; i++) {
        b = insertBTree(b, a[i], i);
        printf("     步骤%d: 插入元素%2d  ", i+1, a[i]);
        dispTree(b);
        printf("
");
    }

    printf(">>> 2.输出2-3树...
");
    dispTree(b);
    printf("
");

    printf(">>> 3.删除关键树...
");
    int e[] = {4, 8};
    for(int i=0; i<2; i++) {
        printf("     步骤%d: 删除元素%2d  ", i+1, e[i]);
        b = deleteBTree(b, e[i]);
        dispTree(b);
        printf("
");
    }
    
    printf(">>> 4.销毁2-3树...
");
    freeTree(b);
    return 0;
}

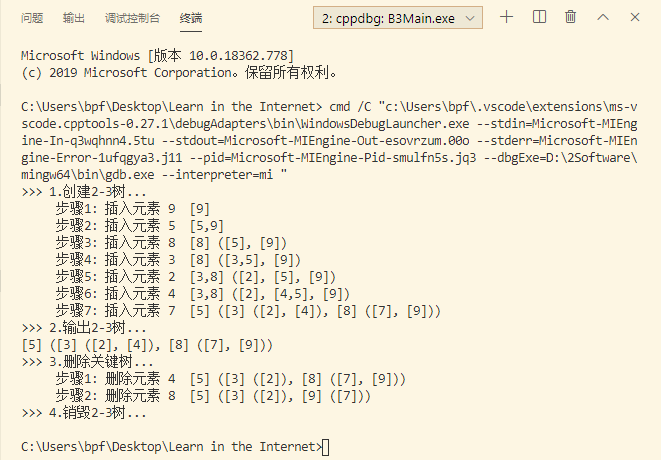
10. 贪心算法实现活动安排

/*
 * @Author: bpf
 * @Date: 2020-06-10 09:42:34
 * @LastEditTime: 2020-06-10 10:49:38
 * @Description: 活动安排 贪心算法实现
 * @FilePath: Learn in the InternetCodeAlgorithmsActivity.cpp
 */ 

/* n个活动  start[]存放开始时间 end[]存放结束时间 play[]存放活动是否入选
    1. 按照结束时间非降序排序数组end
    2. 贪心算法找出结束时间最早的活动，存入play[]
    3. 找出下一个结束时间最早的相容的活动，存入play[]
    4. 循环2、3
    5. 返回总活动数量
*/
#include <stdio.h>
#define MAX 100

void printArray(int n, int a[]) {
    for(int i=0; i<n; i++) {
        printf("%d ", a[i]);
    }
    printf("
");
}

void swit(int *a, int *b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void upSort(int n, int start[], int end[]) {
    int min;
    for(int i=0; i<n-1; i++) {
        min = i;
        for(int j=i+1; j<n; j++) {
            if(end[min] > end[j]) {
                min = j;
            }
        }
        if(min != i) {
            swit(end+min, end+i);
            swit(start+min, start+i);
        }
    }
}

int ActivityManage(int n, int start[], int end[], bool printManage) {
    // play[]置0, 默认所有活动都不安排
    bool play[MAX] = {0};
    // 非降序排序数组end
    upSort(n, start, end);
    // 贪心找出活动
    play[0] = 1;    // 第一个活动被安排
    int count = 1;  // 统计被安排的活动总数
    for(int i=1, j=0; i<n; i++) {
        if(start[i] >= end[j]) {
            play[i] = 1;
            j = i;
            count++;
        }
    }

    // 输出被安排活动详情
    if(printManage) {
        // printArray(n, play);
        printf("被安排活动为：");
        for(int i=0; i<n; i++)
            if(play[i])
                printf("(%d-%d) ", start[i], end[i]);
        printf("
被安排活动总数为：%d", count);
    }

    return count;
}

int main() {
    int start [MAX] = {1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12};
    int end [MAX] =   {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14};
    int n = 11;
    printf("1. 请输入活动个数：");
    scanf("%d", &n);
    printf("2. 请输入每个活动的开始时间与结束时间(空格分开)
");
    for(int i=0; i<n; i++) {
        printf("第%d个活动(开始时间 结束时间)：", i+1);
        scanf("%d %d", &start[i], &end[i]);
    }
    
    ActivityManage(n, start, end, true);

    return 0;
}

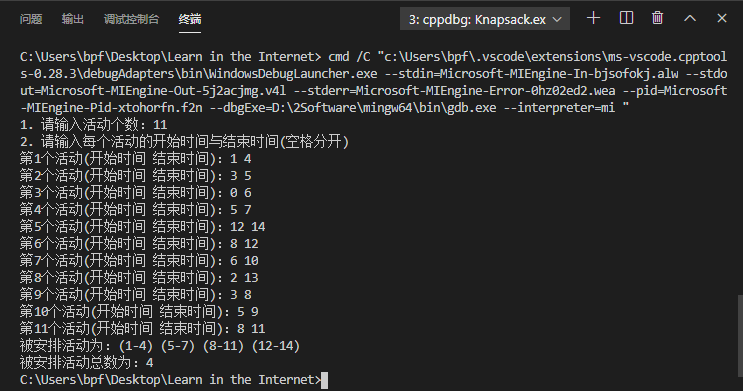
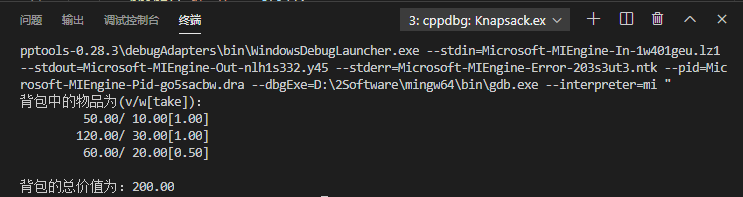
11. 贪心算法实现背包问题

/*
 * @Author: bpf
 * @Date: 2020-06-10 10:29:59
 * @LastEditTime: 2020-06-10 11:11:10
 * @Description: 背包问题 贪心算法实现
 * @FilePath: Learn in the InternetCodeAlgorithmsKnapsack.cpp
 */ 

/*  背包容量为W, 价值为V
    n个物品, 重量分别为w[], 价值为v[]
    1. 按照v/w从大到小排序
    2. 贪心找出性价比最高的物品放入背包
    3. 若背包有空间继续放性价比最高的物品，若无空间结束
    4. 循环2、3
    5. 返回背包总价值V
*/

#include <stdio.h>
#define MAX 100

void printArray(int n, float a[]) {
    for(int i=0; i<n; i++) {
        printf("%6.3f ", a[i]);
    }
    printf("
");
}

void swit(float *a, float*b) {
    float tmp = *a;
    *a = *b;
    *b = tmp;
}

void costSort(int n, float v[], float w[], float cost[]) {
    for(int i=0; i<n; i++) {    // 计算性价比
        cost[i] = v[i] / w[i];
    }

    // 快速排序cost[]
    int min;
    for(int i=0, j; i<n-1; i++) {
        min = i;
        for(j=i+1; j<n; j++) {
            if(cost[min] < cost[j]) {
                min = j;
            }
        }
        if(min != i) {
            swit(cost+min, cost+i);
            swit(v+min, v+i);
            swit(w+min, w+i);
        }
    }
}

float knapsack(int n, float W, float v[], float w[], bool printManage) {
    // take[]置0
    float take[MAX] = {0};      // 存放背包放置i物品的数量
    // 按照性价比排序
    float cost[MAX];            // 存放性价比
    costSort(n, v, w, cost);    // 按照性价比排序
    float V = 0;                // 存放背包的总价值
    // 贪心找出性价比最高的物品
    int i = 0;
    while(w[i] < W) {
        take[i] = 1;
        V += v[i];
        W -= w[i];
        i++;
    }
    // 剩余空间不足一个物品，此时可拆出其中的零件
    take[i] = W / w[i];
    V += take[i] * v[i];

    // 输出被安排活动详情
    if(printManage) {
        // printArray(n, take);
        printf("背包中的物品为(v/w[take])：
");
        for(int i=0; i<n; i++)
            if(take[i] > 0)
                printf("	%6.2f/%6.2f[%4.2f]
", v[i], w[i], take[i]);
        printf("
背包的总价值为：%.2f", V);
    }

    return V;
}


int main() {
    float v[MAX] = {60, 120, 50};
    float w[MAX] = {20, 30, 10};
    int n = 3;
    float W = 50;
    knapsack(n, W, v, w, true);


    return 0;
}