DFS习题

本次学习主要参考算法竞赛入门经典（第二版）。因为DFS本质上还是属于暴力破解，因此从基础的暴力求解法例题学起

---

1、生成1~n的排列

例如n=3时，输出（1,2,3）(1,3,2)（2，1，3）（2，3，1）（3，1，2）（3，2，1）。

尝试用递归的思想解决，先输出所有以1开头的排列，然后输出以2开头的排列……

    public void print_permutation(int n, int[] A, int cur){
        if ( cur == n ){
            for( int i = 0 ; i < n ; i ++ ) System.out.print(A[i]);
        }
        else {
            for ( int i = 1 ; i <= n ; i++){    //尝试在A[cur]中填各种整数i
                int ok = 1;
                for ( int j = 0 ; j < cur ; j ++ )
                    if( A[j] == i ) ok = 0;      //如果i已经在A[0]——A[cur-1]出现过，就不能选了
                if ( ok == 1 ){
                    A[cur] = i;
                    print_permutation(n, A, cur + 1);   //递归调用
                }
            }
        }
    }

上面的代码就是完整的解题过程，可以看到通过最外层的for循环，不断尝试在A[cur]找个位置填入各种整数i，然后递归调用print_permutation函数。因为每一次递归都要调用找个for循环，所以可以理解为从后往前修正，比如A =123，cur=3，然后这个时候无法调用递归函数了，所以跳出最后一轮递归，对cur=2位置再往下循环，此时A[2]没有办法取其他值，所以再跳出递归，检查A[1]位置，发现A[1]还可以取3.然后再进入递归。

结果如下：

---

 2、求一个集合的全部子集

算法描述:
//1、如果遍历完全集，打印出所有被标记为true的元素
//2、否则：
//3、取第depth个元素，即标记为true
//4、继续判断第depth+1个元素
//5、不取第depth个元素，即标记为false
//6、继续判断第depth+1个元素
//如：集合元素为a,b,c
// 把与元素a对应的标记为true,表示要取出
//判断元素b，进入第一层递归，里面就标记b为取出，再进入递归，标记C为取出，再进入递归，打印a,b,c
//退出上一层递归，标记c不取出，进入第二个递归，由于已经遍历完，打印出ab,
//依此类推
//。。。

 代码实现：

public void print_subset(int n, int[] A, int cur, boolean[] B){
        if ( cur == n ){         //判断递归结束条件
            for ( int i = 0 ; i < n ; i ++ ){
                if (B[i])
                    System.out.print(A[i] + " ");
            }
            System.out.println();
            return ;
        }
        else {
            B[cur] = true;
            print_subset(n,A,cur+1,B);
            B[cur] = false;
            print_subset(n,A,cur+1,B);
        }
    }

---

3、八皇后问题

八皇后问题是一个古来而著名的问题，该问题是19世纪著名的数学家高斯同学提出来的。在8*8的国际象棋上摆放八个皇后，使其不能互相的攻击，也就是说，任意的两个皇后不能放在同一行或则是同一个列或者是同一个对角线上，问有多少个摆放的方法。

最简单暴力的方法将问题转化为“从64个格子选一个子集，使得某些子集恰有8个格子，并且该子集中任意两个格子都不在同一行，同一列，同一对角线上”，转化为求解全子集问题，但是时间复杂度太高了。

第二个暴力方法将问题转化为“从64个格子中选择8个”，也不够好。

仔细阅读题目，发现每行每列只能由一个皇后，用C[x]表示第x行皇后的列编号，那么就有8！次枚举。

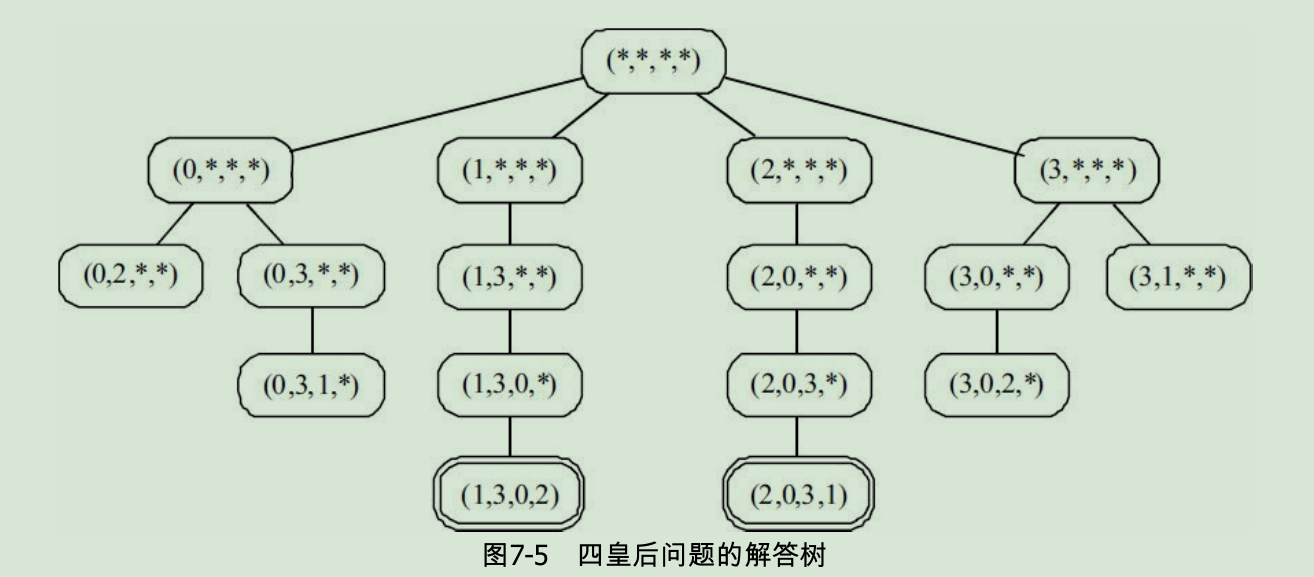
上图是四皇后问题的解答树，在这里解答树可以帮助我们理清递归的过程。根节点（*，*，*，*）表示在（0，1，2，3）行可以任意选择列，因此划分到第一行，（0，*，*，*）代表第0行第0列放一个皇后，因此第一行第一列就不能放皇后了，所以这个节点往下只能是（0，2，*，*）和（0，3，*，*），依次往下分析，最终得到上述的解答树。

在解答树建立过程中，其实我们用到了回溯：在把问题分成若干步骤并递归求解时，如果当前步骤没有合法选择，则函数将返回上一级递归调用。

public class eightqueue {
    int count = 0;
    int queue = 8;
    int[] C = new int[queue];    //C[i]的值是列数，下标是行数

    public static void main(String[] args){
        eightqueue e = new eightqueue();
        e.calcqueue(0);
    }

    public void calcqueue(int cur){
        if ( cur == queue ) count++;  //cur指向行数
        else {
            for ( int i = 0 ; i < queue ; i++ ){    //i代表列数
                int ok = 1;
                C[cur] = i;
                for ( int j = 0 ; j < cur ; j ++ ){    //检查与前面的皇后有没有冲突
                    if ( C[cur] == C[j] || cur-C[cur] == j-C[j] || cur+C[cur] == j+C[j] ) {
                        ok = 0;
                        break;
                    }
                }
                if ( ok == 1 ) calcqueue(cur+1);
            }
        }
        System.out.println(count);
    }
}

最后求解8皇后有92种方法。

上述方法还可以再优化一下，使用另外的visited数组记录下已经放置的皇后占据哪些列，主对角线和副对角线。

public class eightqueue {
    static int count = 0;
    int queue = 8;
    int[] C = new int[queue];    //C[i]的值是列数，下标是行数
    boolean[][] visited = new boolean[3][queue*2]; //visited的3行分别记录摆放好的皇后占据的列、主对角线、副对角线，注意这里列数要扩大

    public static void main(String[] args){
        eightqueue e = new eightqueue();
        e.calcqueue(0);
        System.out.println(count);
    }

    public void calcqueue(int cur){
        if ( cur == queue ) count++;  //cur指向行数
        else {
            for ( int i = 0 ; i < queue ; i++ ){    //i代表列数
                if ( !visited[0][i] && !visited[1][cur+i] && !visited[2][cur-i+queue] ){
                    C[cur] = i;
                    visited[0][i] = visited[1][cur+i] = visited[2][cur-i+queue] = true;
                    calcqueue(cur+1);
                    visited[0][i] = visited[1][cur+i] = visited[2][cur-i+queue] = false;  //回溯的过程一定要把visited状态恢复原样
                }
            }
        }
    }
}

注意：如果在回溯法中使用了辅助的全局变量，则一定要及时把它们恢复原状。特别地，若函数有多个出口，则需在每个出口处恢复被修改的值。

---

4、素数环

输入正整数n，把整数1~n组成一个环，要求每两个相邻整数之和为素数。输出从1开始逆时针排列。

样例输入：
6
样例输出：
1 4 3 2 5 6
1 6 5 2 3 4

分析：首先想到的暴力枚举法，将所有的可能组合都枚举出来，然后一一判断是否是素数环，但是这样时n！时间复杂度，太高了。

因此可以试试DFS，加上回溯，降低时间复杂度。

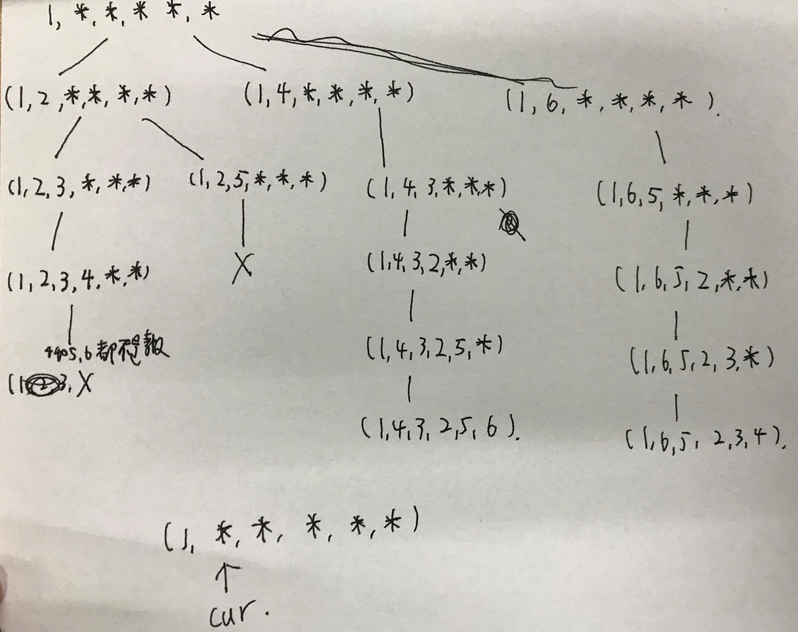
上图是n=6时的解答树。

从上图可以看到我们需要一个用来记录是否访问的visited数组，一个用来保存结果的A数组。同时要注意这时cur初始位置应该是1，而不是0。

public class PrimeRing {

    int n = 6;
    int[] A = new int[n];
    boolean visited[] = new boolean[n+1];   //注意这里visited数组，visited[i]代表i是否被访问，因此长度应该是n+1

    public static void main(String[] args){
        PrimeRing p = new PrimeRing();
        p.calcprimering(1);
    }

        public void calcprimering(int cur){
        if ( cur == n && isprime(A[0] + A[n-1]) ){   //递归结束条件
            for ( int i : A ) System.out.print(i);
            System.out.println();
        }
        else {
            A[0] = 1;
            for ( int i = 2 ; i <= n ; i ++ ){
                if ( !visited[i] && isprime(i + A[cur-1]) ){
                    A[cur] = i;
                    visited[i] = true;
                    calcprimering(cur+1);
                    visited[i] = false;        //回溯时恢复原状态
                }
            }
        }
    }

    private boolean isprime(int num) {
        for ( int i = 2 ; i <= Math.sqrt(num) ; i++ ){
            if ( num % i == 0 ) return false;
        }
        return true;
    }
}