我之前对于KMP算法理解的也不是很到位,如果很长时间不写KMP的话,代码就记不清了,今天刷leetcode的时候突然决定干脆把它彻底总结一下,这样即便以后忘记了也好查看。所以就有了这篇文章。
本文在于帮助大家理解KMP算法的编码实现,假设大家已经明白了KMP算法的原理。如果还不太理解,请参考阮一峰老师的这篇博文,写的不能更清楚了:)
好吧,现在让我们正式开始。
首先,我们要简单回顾一下KMP算法的流程,假设要在串s中找串p,如下图所示。现在已经匹配了有一段了(绿色部分),但是在某个地方发生了失配(图中红色和黄色小块)。
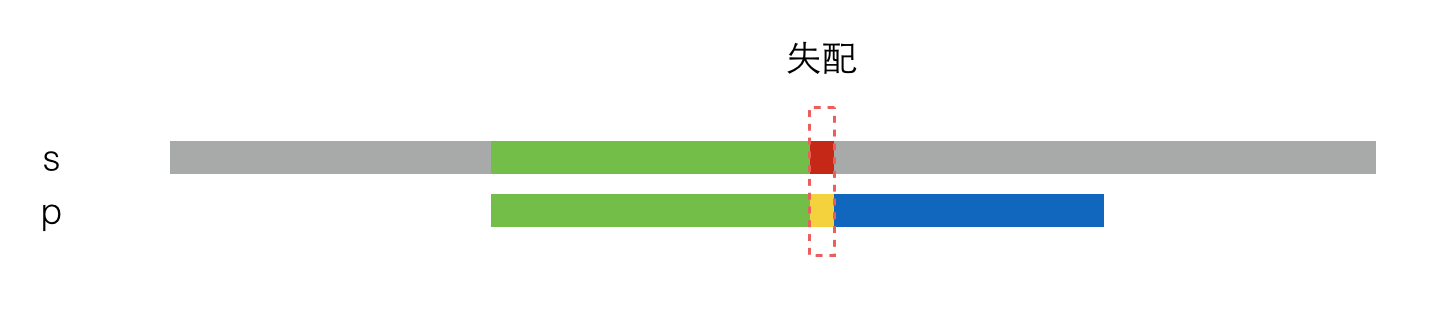
于是,将p串右移一定距离,再次尝试匹配,如下图所示。
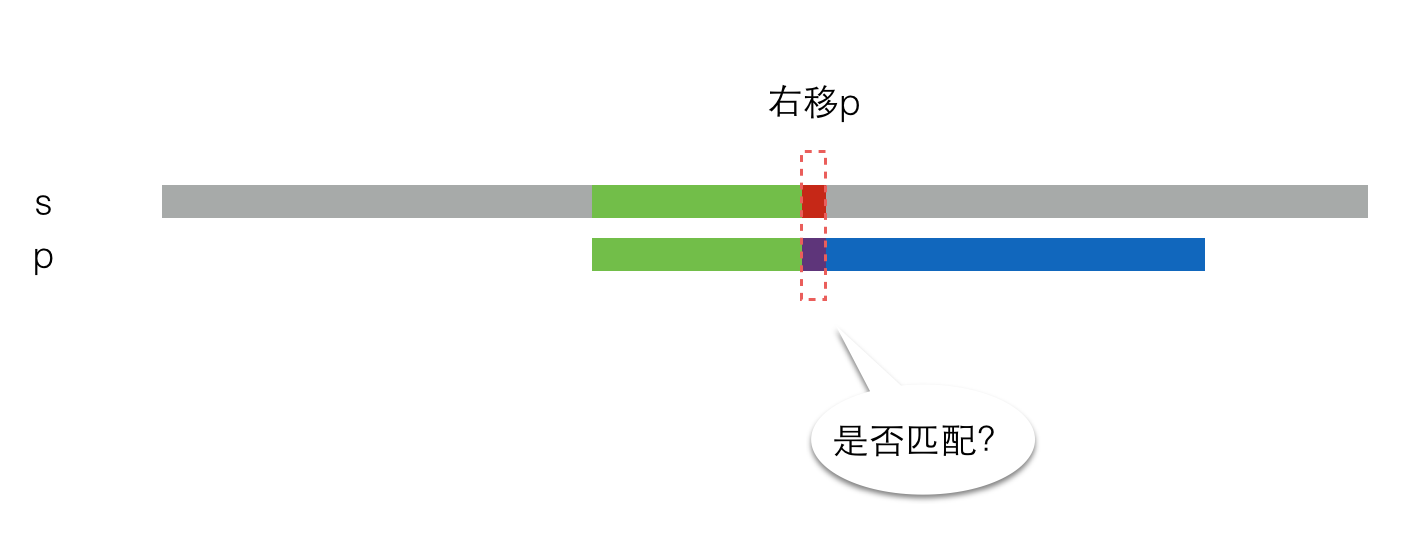
此时,有两种情况。第一种情况是这两块恰好匹配,那么继续匹配下一个元素,就像这样:
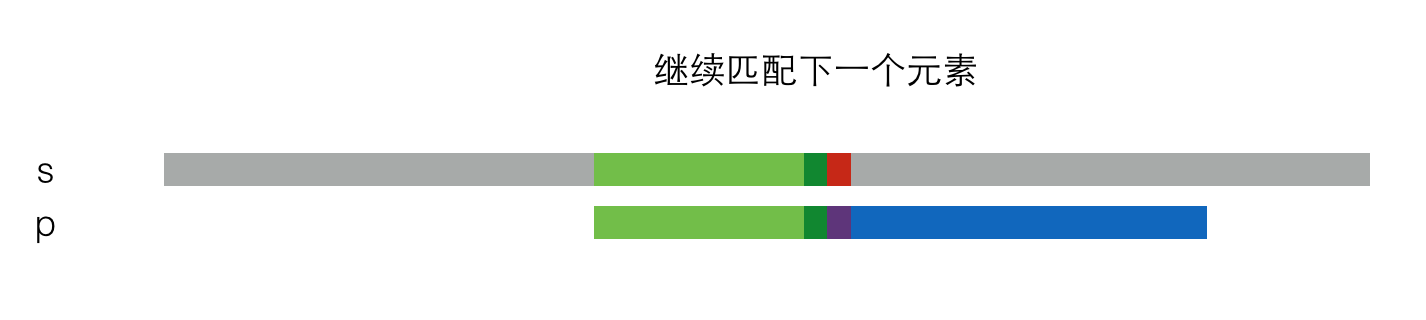
另一种情况是不匹配,那么p串就要再次右移一定距离,并再次尝试是否匹配,就像这样:
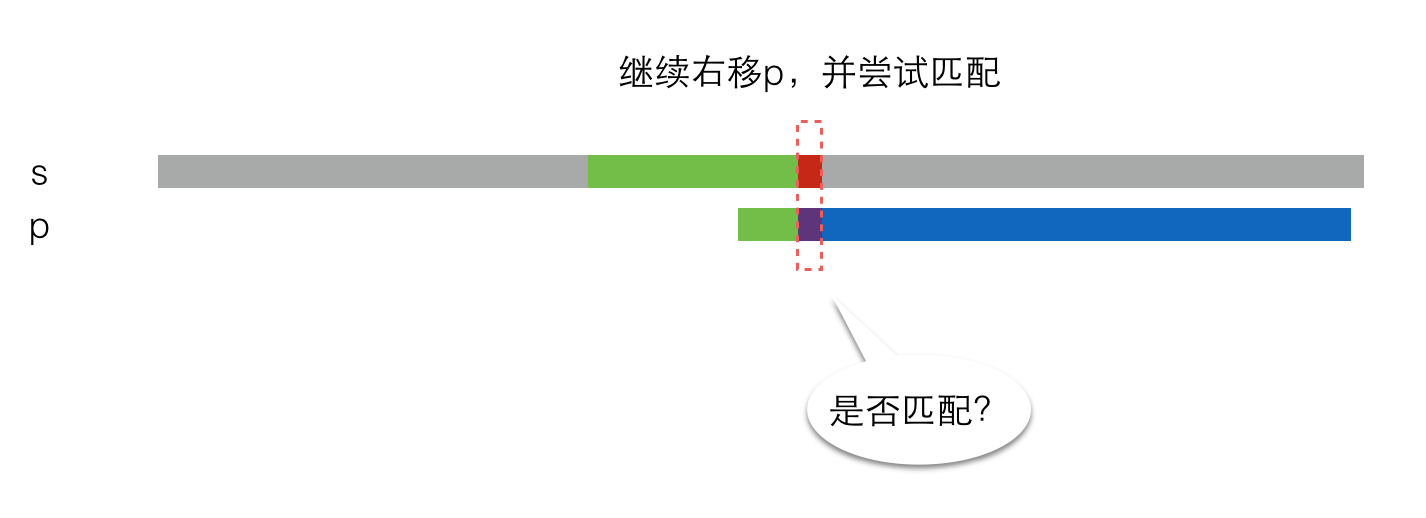
那么,当失配发生时,p串应该向右移动多长的距离呢?看下图:
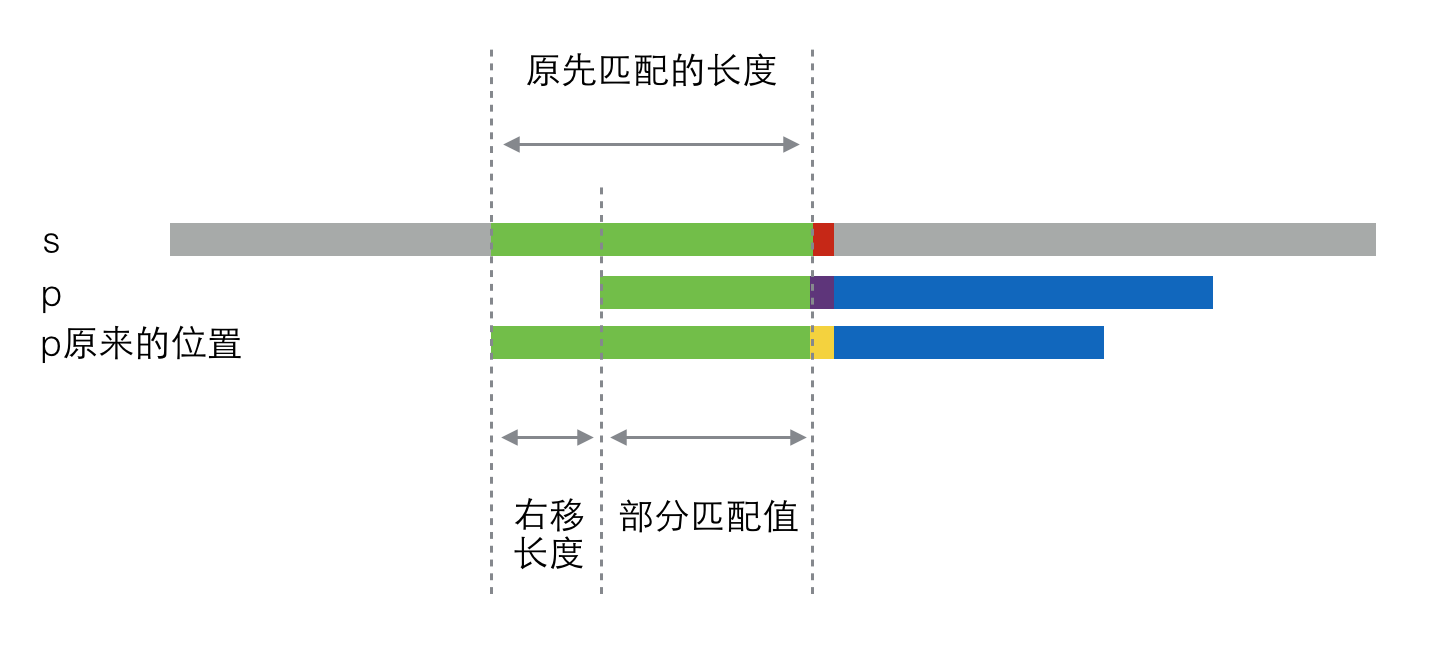
很明显,右移的距离 = 原来匹配部分的长度(绿色部分)- 部分匹配值
PS:"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度
(如果不明白什么是“部分匹配值”,请参本文开头介绍的阮一峰老师的KMP科普文)
所以,要实现KMP算法,必须要计算出p串各个子串的部分匹配长度。通常KMP算法教材所说的next数组(或者其他名字)本质上指的就是这个“部分匹配值”,next[i]表示从0到i的子串的部分匹配值。有时候将next[0]设为-1,那是为了简化编程实现,他们没有本质区别,优化的next数组另说。
那么现在问题来了,怎么求这个next数组呢?
因为知道next数组的意义,所以最笨的方法就是枚举+检验找出部分匹配值,当然这样做显得太low了。其实你可以把这个问题单独考虑成一个动态规划问题——“求一个字符串s的最大前缀后缀匹配长度”。这样想也许有助于你去理解求next数组的代码。对了,有些地方我也觉得写的挺绕口,没办法。。不过只要你能理解我的意思就行,没必要每个词细扣。
好的,现在让我们试着去分析一下如何求next数组。
还是老办法,先假设我们已经求出next[0]到next[i]的值,而现在要求next[i+1]。如下图所示,绿色的部分是next[i]表示的部分匹配长度,也就是从0到i的子串的部分匹配长度。红色小块代表第i+1个元素。
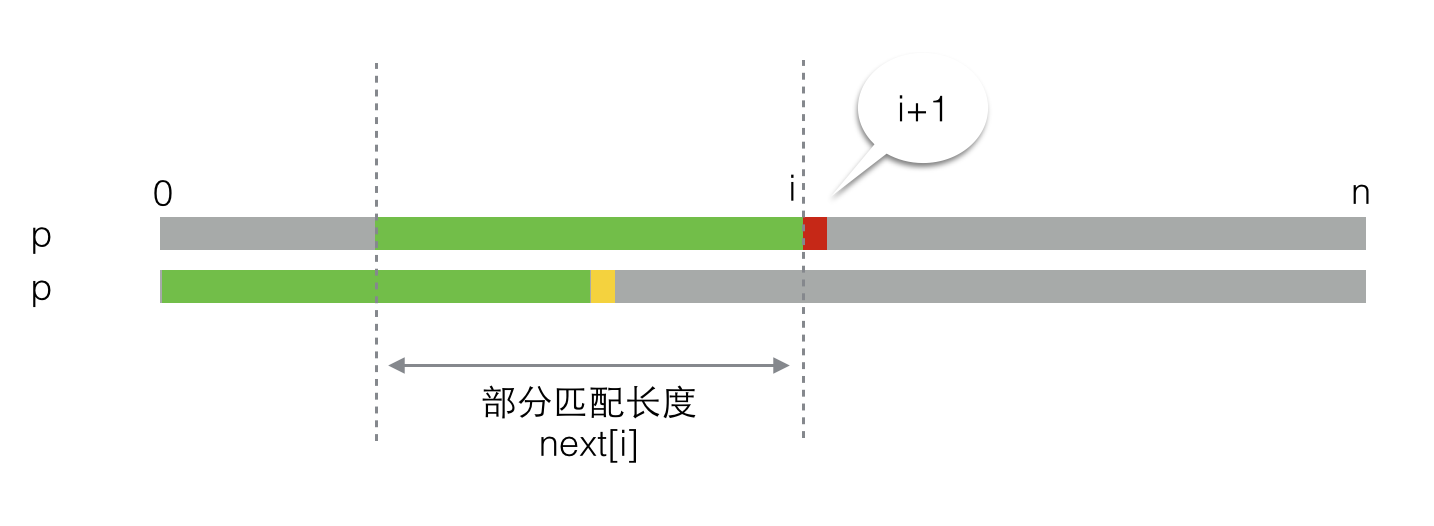
上面的图看着有些别扭,没关系,调整一下,把其中绿色匹配的部分对齐,变成下面这个样子:
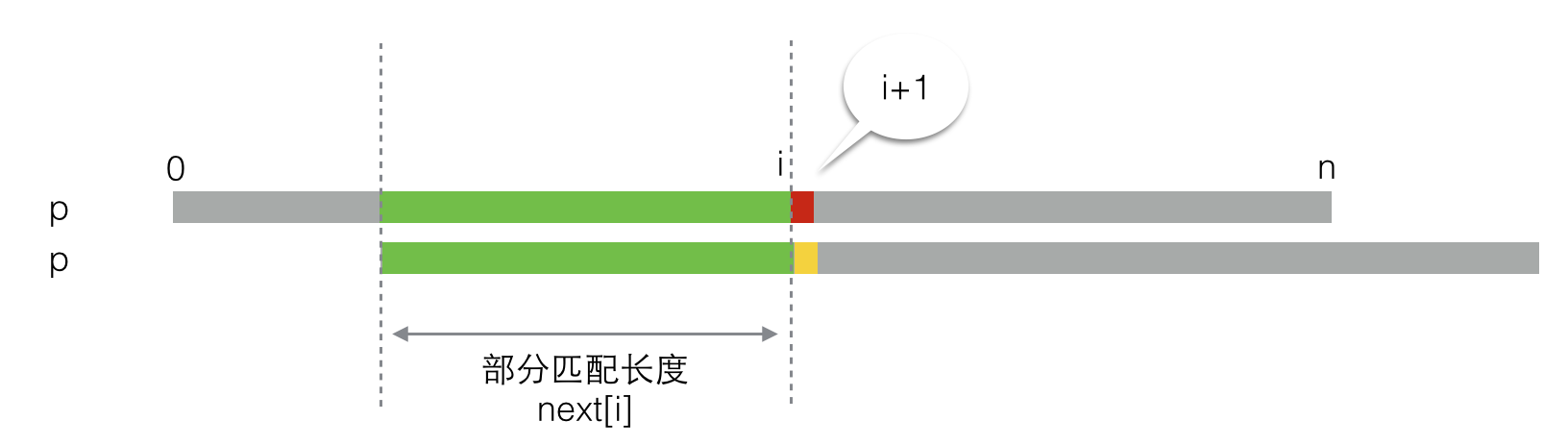
那么此时在比较红色和黄色小块的时候也会遇到两种情况:
第一种情况,二者匹配,这是比较好的情况。在这种情况下,next[i+1] = next[i] + 1,然后继续求next[i+2],就像下图所示的那样。
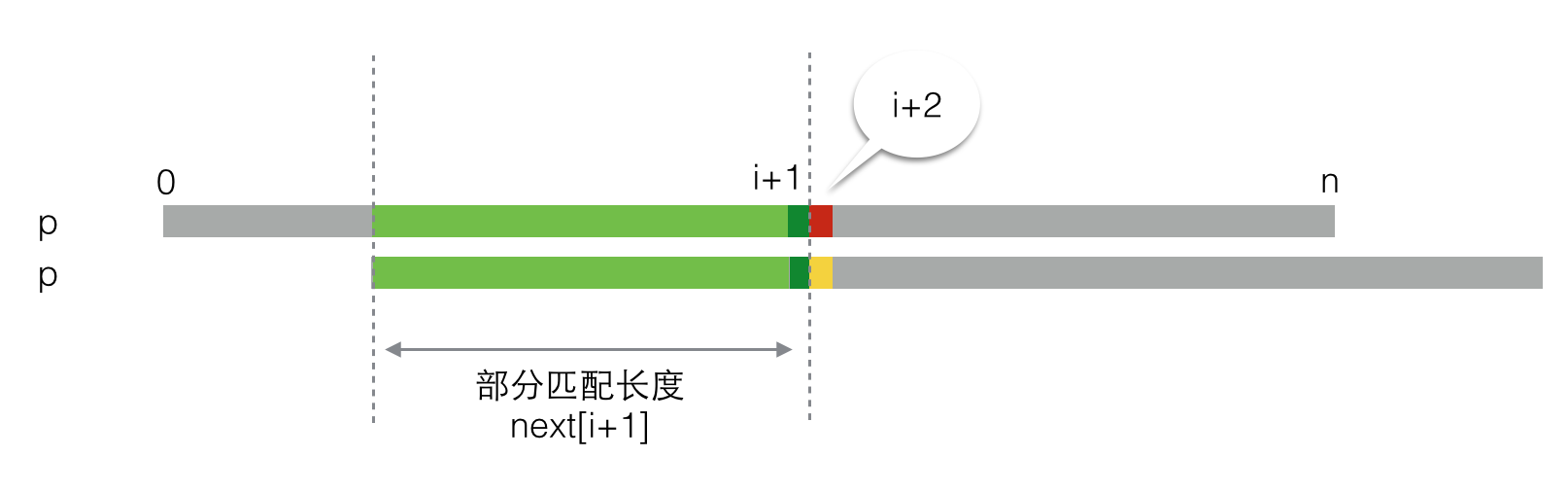
第二种情况,二者不匹配。如下图所示,此时next[i+1]等于多少就没那么明显了,这里就是求解next唯一的难点。
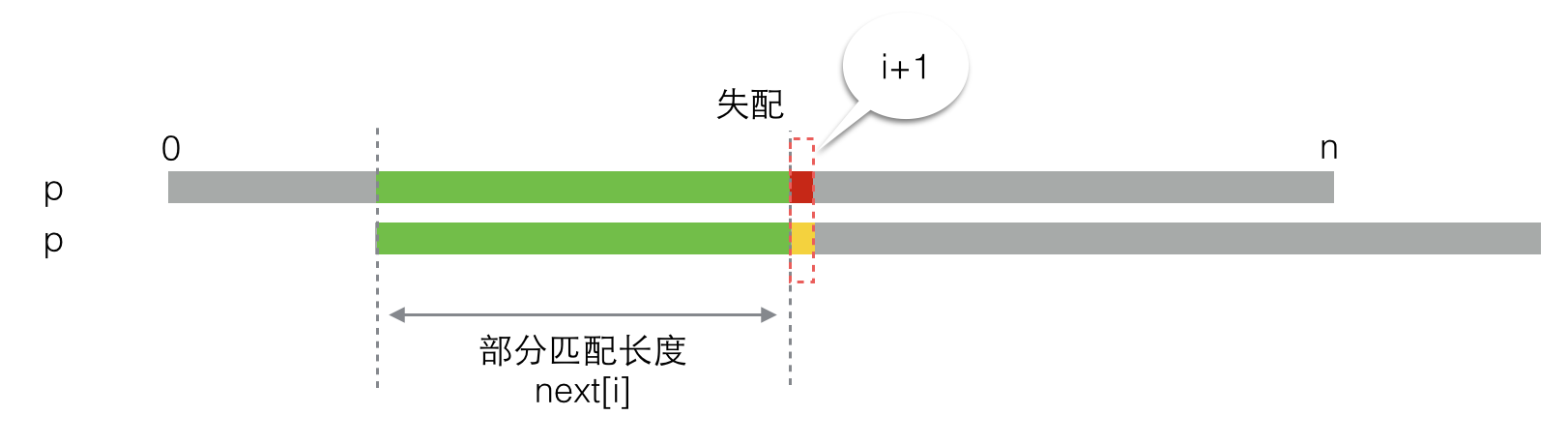
让我们先把怎么求next[i+1]的问题放在一边,现在假设通过某种方法,我们已经求出了next[i+1]的值,那么就有:
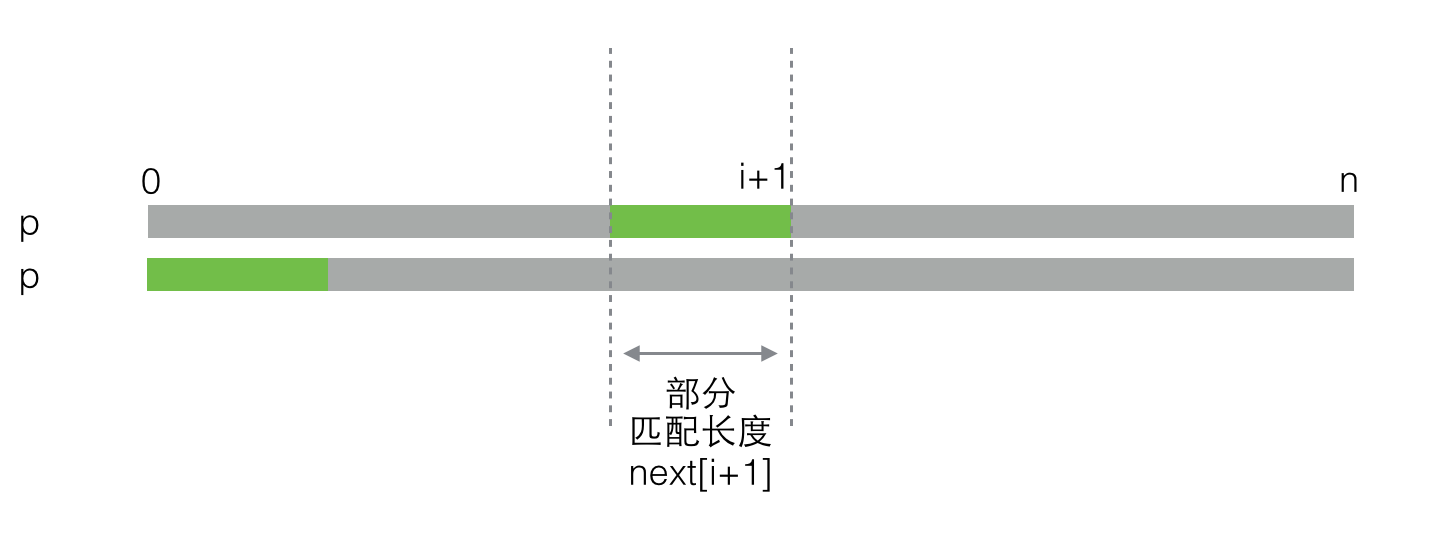
同样,绿色的部分代表next[i+1]的值,即从0到i+1的子串的部分匹配长度。我们再把上图调整一下,让绿色的部分对齐,就像下图一样。
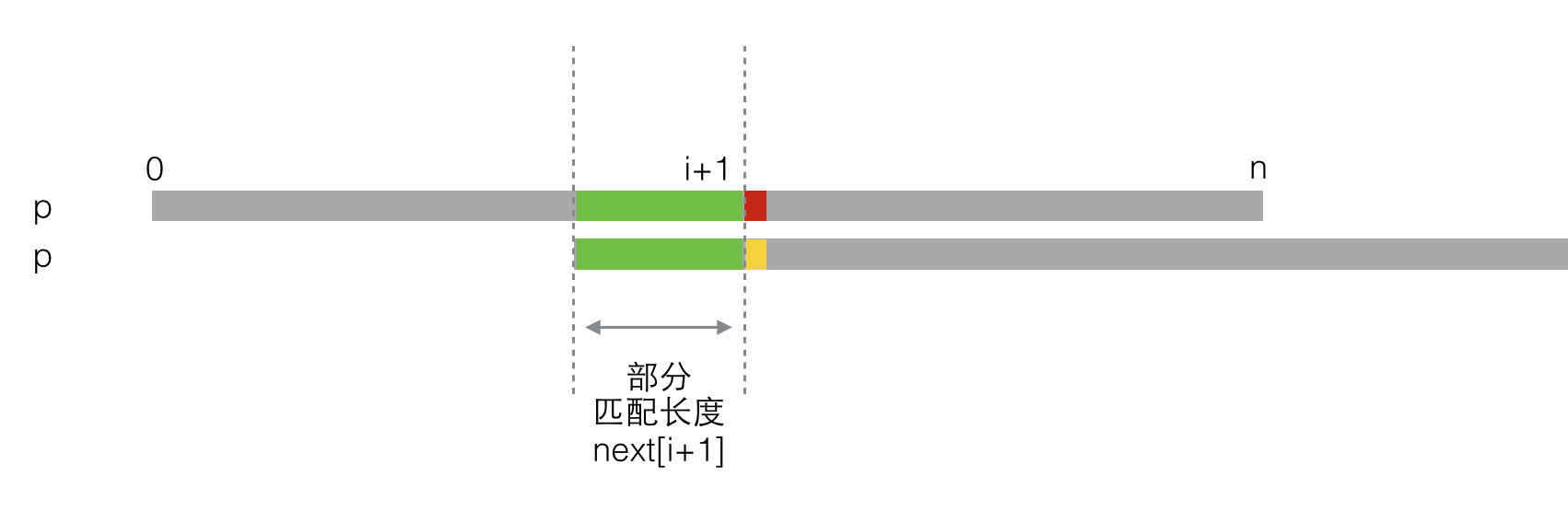
你有没有觉得这个过程很像KMP算法在做字符串匹配?你可以对比本文开头回顾KMP匹配的过程。说实话当我第一次发现这个现象的时候挺震惊的,毕竟,我们为了使用KMP算法才去求next数组,但是在求next数组的时候已经在应用KMP算法做字符串匹配了!
现在你知道怎么求next[i+1]了吧?因为求next[i+1]的过程本身就是一个KMP匹配过程。
好,现在回到求next[i+1]的地方,此时失配了(红色和黄色不匹配),就像这样:
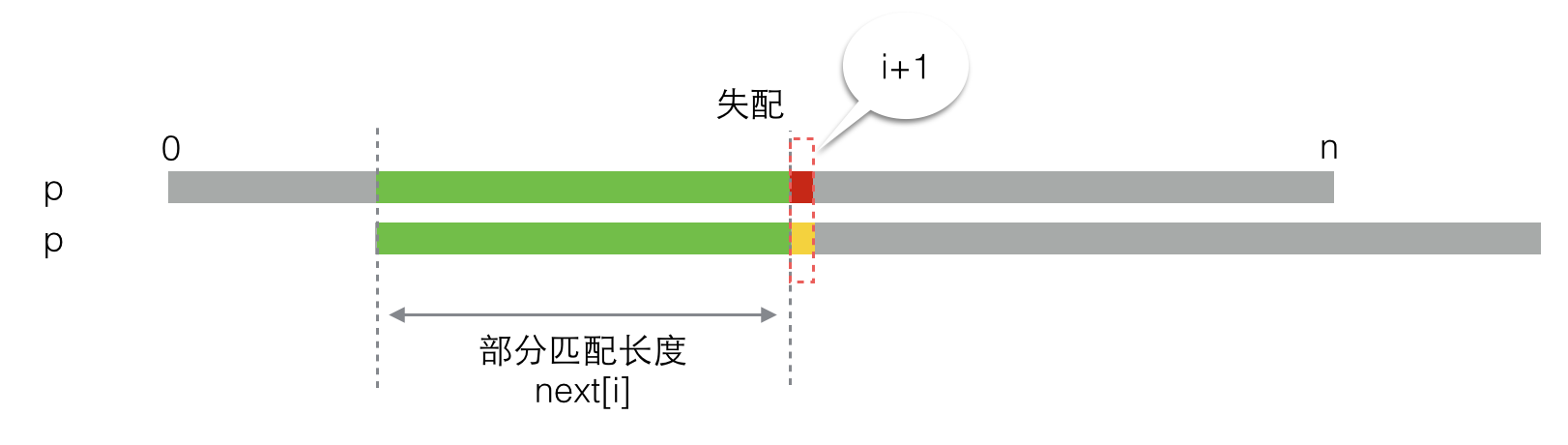
于是我们将p右移一段距离,为了区分,这里把下面的p称作p',他们其实是一样的。

同样地,我们有:部分匹配长度next[i] = 右移长度 + 部分匹配长度x
请注意,在这里,“右移长度”是我们想要求出来的未知量。不过这里除了“右移长度”外,还有另一个变量不清楚——“部分匹配长度x”。它又等于多少呢?如果我们将上图再画详细一些:
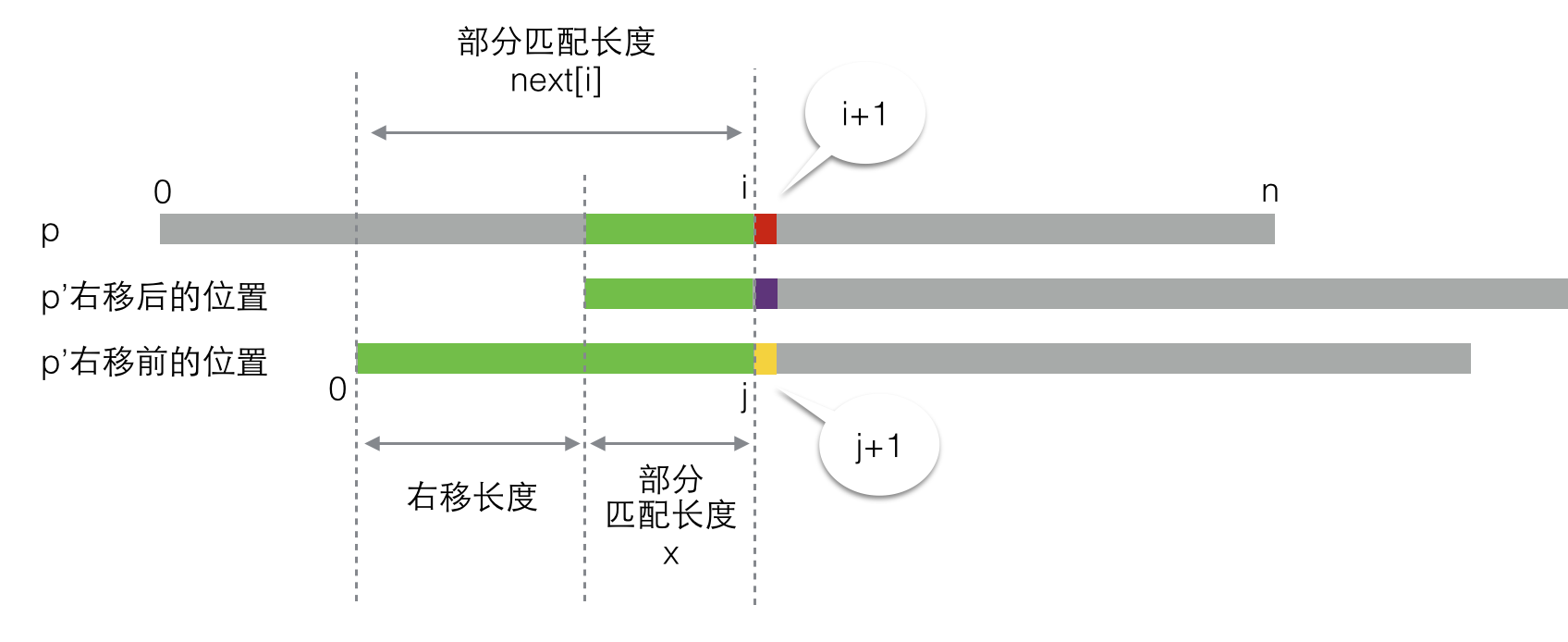
我们可以假设p’在右移前,匹配的部分是从0到j的子串,那么“部分匹配长度x”就是子串p[0..j]的部分匹配长度(注:p[0..j]代表p的从0开始到j结束的子串,下同)。这里有些绕,所以我又画了一张图:
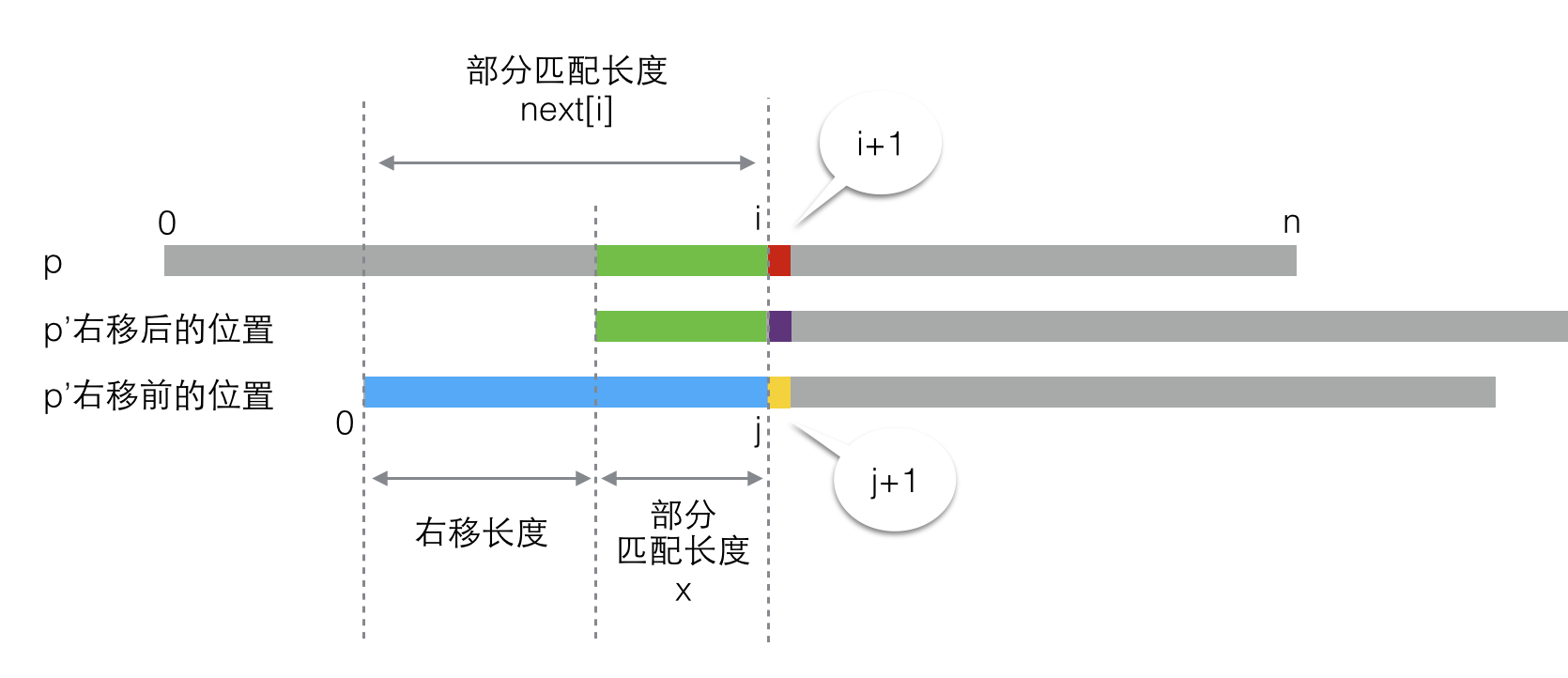
这下就很清楚了,“部分匹配长度x” = 上图中蓝色部分的部分匹配长度 = next[j]。请一定保证你已经完全理解了以上的所有内容然后再继续,这很重要。
注意,next[j]是已知的(因为j一定小于i,而且我们假设next[0]到next[i]事先已经求出来了),所以回想刚才的公式 next[i] = 右移长度 + next[j],我们可以计算出“右移长度了”!
可别高兴太早,j是多少呢?
其实 j = next[i]。回想next数组的定义,next[i]表示子串p[0..i]的部分匹配长度,而j刚好就是子串p[0..i]的部分匹配长度。补充一下,这里不是很严谨,因为数组从0编号,所以实际上next[i] = j + 1,whatever,你理解我的意思就好。
现在,我们求出了“右移长度”,于是将p右移,就像这样:
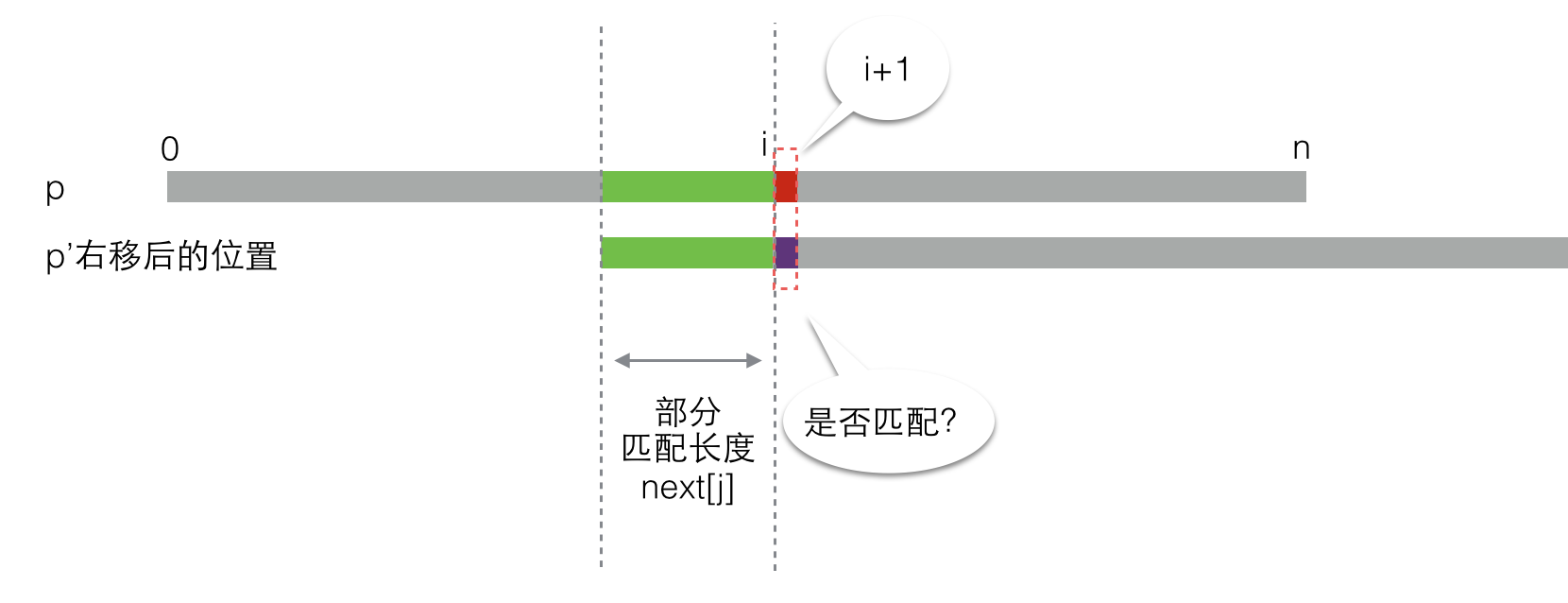
好了,现在似乎又回到了一开始的时候(此时j = next[i])。你又会遇到两种情况。。。于是就这么递归下去了。
好了,以上就是求next数组的全部过程!如果你每一步都弄明白了,相信现在你理解代码就完全没有问题了。
让我们简单看看求next数组的代码。
这里为了方便处理特殊情况,在next数组前加了一个哨兵变量,即next[0] = -1,这样当访问next[0]的时候就知道已经没法再右移了,省去了额外对数组边界的判断。
1 void compute_next(char *p, int *next) { 2 int i, j; 3 i = 0; 4 j = -1; 5 next[0] = -1; 6 while (p[i] != '�') { 7 if (j < 0 || p[i] == p[j]) { 8 i++; 9 j++; 10 next[i] = j; 11 } 12 else 13 j = next[j]; 14 } 15 }
第7行是处理第一种情况,第13行是处理第二种情况,就这么简单。
下面是KMP匹配部分的代码,打印出串s中所有匹配串p的起始索引。这里必须要至少知道串p的长度,因为需要计算匹配的索引(16行)。
1 void kmp(char *s, char *p, int *next) { 2 int m, n; 3 int i, j; 4 m = strlen(s); 5 n = strlen(p); 6 i = 0; 7 j = 0; 8 while (i < m && j < n) { 9 if (j < 0 || s[i] == p[j]) { 10 i++; 11 j++; 12 } 13 else 14 j = next[j]; 15 if (j == n) { 16 printf("match at position %d ", i - n); 17 j = next[j]; 18 } 19 } 20 }
是不是和求next数组的代码很像?
最后再啰嗦一句,这也是我在做kmp题的时候被坑过的地方。如果用string保存字符串,那么在比较i、j和字符串的长度s.length()、p.length()时要加上类型转换。即把字符串长度转换成int型,因为字符串长度是无符号类型。如果不加类型转换,当j=-1时,j < p.length()始终是false。
大致总结一下求next数组的特点:
- 求next数组和KMP字符串匹配的过程是一样的
- 求next数组是一个递归过程
全文完