我们将先描述卷积神经⽹络中卷积层和池化层的⼯作原理,并解释填充、步幅、输⼊通道和输出通道的含义。掌握了这些基础知识以后,我们将探究数个具有代表性的深度卷积神经⽹络的设计思路。
卷积神经⽹络是含有卷积层(convolutional layer)的神经⽹络,以常见的二维卷积层为例,它有⾼和宽两个空间维度,常⽤来处理图像数据,虽然卷积层得名于卷积(convolution)运算,但我们通常在卷积层中使⽤更加直观的互相关(crosscorrelation)运算。⼀个⼆维输⼊数组和⼀个⼆维核(kernel)数组通过互相关运算输出⼀个⼆维数组。

在⼆维互相关运算中,卷积窗口从输⼊数组的最左上⽅开始,按从左往右、从上往下的顺序,依次在输⼊数组上滑动。当卷积窗口滑动到某⼀位置时,窗口中的输⼊⼦数组与核数组按元素相乘并求和,得到输出数组中相应位置的元素。

自己定义一个互相关运算:
def corr2D(x,k): hight , width = k.shape y = nd.zeros((x.shape[0] - hight + 1 , x.shape[1] - width + 1)) for i in range(y.shape[0]): for j in range(y.shape[1]): y[i,j] = (x[i:i+hight,j:j+width]*k).sum() return y
x = nd.array([[0,1,2],[3,4,5],[6,7,8]]) k = nd.array([[0,1],[2,3]]) y = corr2D(x,k) y
结果是:
[[19. 25.] [37. 43.]] <NDArray 2x2 @cpu(0)>
⼆维卷积层输出的⼆维数组可以看作是输⼊在空间维度(宽和⾼)上某⼀级的表征,也叫特征图(featuremap)。影响元素
x的前向计算的所有可能输⼊区域(可能⼤于输⼊的实际尺⼨)叫做x
的感受野(receptivefield)。我们使⽤⾼和宽为3的输⼊与⾼和宽为2的卷积核得到⾼和宽为2的输出。⼀般来说,假设输⼊
形状是nh×nw,卷积核窗口形状是kh×kw,那么输出形状将会是:
(nh - kh + 1) * (nw - kw + 1)
填充(padding)是指在输⼊⾼和宽的两侧填充元素(通常是0元素)。我们在原输⼊⾼和宽的两侧分别添加了值为0
的元素,使得输⼊⾼和宽从3变成了5,并导致输出⾼和宽由2增加到4。
⼀般来说,如果在⾼的两侧⼀共填充ph⾏,在宽的两侧⼀共填充pw列,那么输出形状将会是
(nh - kh + ph + 1) * (nw - kw + pw + 1)
在很多情况下我们为了保证输出和输入形状一样,就会取ph = kh - 1 , pw = kw - 1 , 例如:当kh是奇数 就会在高的两侧加上ph/2行,当ph是偶数就会在两侧加上[ph-1]/2
行,所以我们卷积神经网络的卷积核维数通常取得是奇数1, 3 , 5 , 7,这样的话,在输入网络中两侧(上下)填充的维数就是一样的
步幅(stride)
卷积窗口从输⼊数组的最左上⽅开始,按从左往右、从上往下的顺序,依次在输⼊数组上滑动。我们将每次滑动的⾏数和列数称为。
当高上的步幅是sh, 宽上的步幅是sw,则输出形状是:
[(nh-kh+ph+sh)/sh] * [(nw-kw+pw+sw)/sw]
通道channel:
彩色图像除了长宽两个维度外还有一个颜色维度(RGB),假设彩色图像的宽w和高h(像素),那么他在内存中可以表示为3*h*w的多维数组。我们把这个3的这一维度称为通道维。
当输⼊数据含多个通道时,我们需要构造⼀个输⼊通道数与输⼊数据的通道数相同的卷积核,从而能够与含多通道的输⼊数据做互相关运算。假设输⼊数据的通道数为ci,那么卷积核的输⼊通道数同样为ci。设卷积核窗口形状为kh×kw。当ci=1时,我们知道卷积核只包含⼀个形状为kh×kw的⼆维数组。当ci>1时,我们将会为每个输⼊通道各分配⼀个形状为kh×kw的核数组。把这ci个数组在输⼊通道维上连结,即得到⼀个形状为ci×kh×kw的卷积核。由于输⼊和卷积核各有ci个通道,我们可以在各个通道上对输⼊的⼆维数组和卷积核的⼆维核数组做互相关运算,再将这ci个互相关运算的⼆维输出按通道相加,得到⼀个⼆维数组。这就是含多个通道的输⼊数据与多输⼊通道的卷积核做⼆维相关运算的输出。
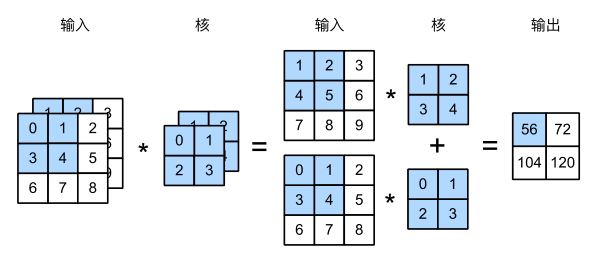
图展⽰了含2个输⼊通道的⼆维互相关计算的例⼦。在每个通道上,⼆维输⼊数组与⼆维核数组做互相关运算,再按通道相加即得到输出。图5.4中阴影部分为第⼀个输出元素及其计算所使⽤的输⼊和核数组元素:(1×1+2×2+4×3+5×4)+(0×0+1×1+3×2+4×3)=56。
如下图展⽰了使⽤输⼊通道数为3、输出通道数为2的1×1卷积核的互相关计算。值得注意的是,输⼊和输出具有相同的⾼和宽。输出中的每个元素来⾃输⼊中在⾼和宽上相同位置的元素在不同通道之间的按权重累加。假设我们将通道维当做是特征维,将⾼和宽维度上的元素当成数据样本,那么1×1卷积层的作⽤与全连接层等价。

在之后的模型⾥我们将会看到1×1卷积层被当做保持⾼和宽维度形状不变的全连接层使⽤。于是,我们可以通过调整⽹络层之间的通道数来控制模型复杂度。
