BFS_拓扑排序 使用图遍历思想也是OK的 虽然代码多了点

127. 拓扑排序

中文

English

给定一个有向图，图节点的拓扑排序定义如下:

• 对于图中的每一条有向边 A -> B , 在拓扑排序中A一定在B之前.
• 拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.

针对给定的有向图找到任意一种拓扑排序的顺序.

样例

例如以下的图:

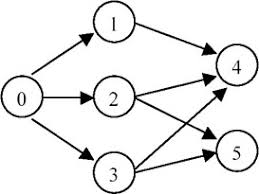
拓扑排序可以为:

[0, 1, 2, 3, 4, 5]
[0, 2, 3, 1, 5, 4]

挑战

能否分别用BFS和DFS完成？

说明

有关图的表示详情请看这里

注意事项

你可以假设图中至少存在一种拓扑排序

class Solution:
    """
    @param graph: A list of Directed graph node
    @return: Any topological order for the given graph.
    """
    def topSort(self, graph):
        node_to_indegree = self.get_indegree(graph)

        # bfs
        order = []
        start_nodes = [n for n in graph if node_to_indegree[n] == 0]
        queue = collections.deque(start_nodes)
        while queue:
            node = queue.popleft()
            order.append(node)
            for neighbor in node.neighbors:
                node_to_indegree[neighbor] -= 1
                if node_to_indegree[neighbor] == 0:
                    queue.append(neighbor)
                
        return order
    
    def get_indegree(self, graph):
        node_to_indegree = {x: 0 for x in graph}

        for node in graph:
            for neighbor in node.neighbors:
                node_to_indegree[neighbor] += 1
                
        return node_to_indegree

from collections import deque


class Solution:
    """
    @param: graph: A list of Directed graph node
    @return: Any topological order for the given graph.
    """
    def topSort(self, graph):
        # write your code here
        if not graph:
            return []
        
        def compute_indegres(graph):
            ans = {}
            for n in graph:
                if n not in ans:
                    ans[n] = 0
                for neighbor in n.neighbors:
                    ans[neighbor] = ans.get(neighbor, 0) + 1
            return ans

            
        def get_indegres0(indegrees):
            return [n for n in indegrees if indegrees[n] == 0]
                                    
        def sorted_nodes(init_nodes, indegrees):
            ans = []
            seen = set(init_nodes)
            q = deque(init_nodes)
            
            while q:
                n = q.popleft()
                ans.append(n)
                
                for node in n.neighbors:
                    indegrees[node] -= 1
                    
                nodes0 = get_indegres0(indegrees)
                for node in nodes0:
                    if node not in seen:
                        q.append(node)
                        seen.add(node)
                        
            return ans
                
        indegrees = compute_indegres(graph)
        init_nodes = get_indegres0(indegrees)
        
        return sorted_nodes(init_nodes, indegrees)

 =】