动态规划算法模板和demo

366. 斐波纳契数列

中文

English

查找斐波纳契数列中第 N 个数。

所谓的斐波纳契数列是指：

• 前2个数是 0 和 1 。
• 第 i 个数是第 i-1 个数和第i-2 个数的和。

斐波纳契数列的前10个数字是：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ...

样例

样例  1:
	输入:  1
	输出: 0
	
	样例解释: 
	返回斐波那契的第一个数字，是0.

样例 2:
	输入:  2
	输出: 1
	
	样例解释: 
	返回斐波那契的第二个数字是1.

class Solution:
    """
    @param n: an integer
    @return: an ineger f(n)
    """
    def fibonacci(self, n):
        # write your code here
        if n == 1:
            return 0
        if n == 2:
            return 1
            
        dp = [0]*n
        dp[1] = 1
        for i in range(2, n):
            dp[i] = dp[i-1]+dp[i-2]
        return dp[n-1]

 最原始的DP！！！

在测试数据中第 N 个斐波那契数不会超过32位带符号整数的表示范围

纯用递归会超时，如果用带有记忆化的递归就可以，使用循环和记忆化递归的时间复杂度一样，都是O(n)。

优化：

class Solution:
    def fibonacci(self, n):
        a = 0
        b = 1
        for i in range(n - 1):
            a, b = b, a + b
        return a

110. 最小路径和

中文

English

给定一个只含非负整数的m*n网格，找到一条从左上角到右下角的可以使数字和最小的路径。

样例

样例 1:
	输入:  [[1,3,1],[1,5,1],[4,2,1]]
	输出: 7
	
	样例解释：
	路线为： 1 -> 3 -> 1 -> 1 -> 1。


样例 2:
	输入:  [[1,3,2]]
	输出:  6
	
	解释:  
	路线是： 1 -> 3 -> 2

注意事项

你在同一时间只能向下或者向右移动一步

Dp[i][j] 存储从（0， 0） 到（i, j）的最短路径。
Dp[i][j] = min(Dp[i-1][j]), Dp[i][j-1]) + grid[i][j];

class Solution:
    """
    @param grid: a list of lists of integers
    @return: An integer, minimizes the sum of all numbers along its path
    """
    def minPathSum(self, grid):
        # write your code here
        row, col = len(grid), len(grid[0])
        dp = [[0]*col for i in range(row)]
        
        dp[0][0] = grid[0][0]
        for i in range(1, row):
            dp[i][0] = grid[i][0]+dp[i-1][0]
        
        for j in range(1, col):
            dp[0][j] = grid[0][j]+dp[0][j-1]
        
        for i in range(1, row):
            for j in range(1, col):
                dp[i][j] = min(dp[i-1][j], dp[i][j-1])+grid[i][j]
        
        return dp[row-1][col-1]

 记得画图，二维矩阵。

dp的过程，初始化，状态转移方程：

空间优化：

滚动数组代码，java，考试不用这么肝，面试有明确思路即可：

public class Solution {
    /**
     * @param grid: a list of lists of integers.
     * @return: An integer, minimizes the sum of all numbers along its path
     */
    public int minPathSum(int[][] A) {
        if (A == null || A.length == 0 || A[0].length == 0) {
            return 0;
        }
        
        int m = A.length, n = A[0].length;
        int[][] f = new int[2][n];
        int i, j;
        int old, now = 0; // f[i] is stored in rolling array f[0]
        for (i = 0; i < m; ++i) {
            old = now;
            now = 1 - now; // 0 --> 1, 1 --> 0
            
            for (j = 0; j < n; ++j) {
                if (i == 0 && j == 0) {
                    f[now][j] = A[0][0];
                    continue;
                }
                
                f[now][j] = Integer.MAX_VALUE;
                if (i > 0) {
                    f[now][j] = Math.min(f[now][j], f[old][j]);
                }
                
                if (j > 0) {
                    f[now][j] = Math.min(f[now][j], f[now][j - 1]);
                }
                
                f[now][j] += A[i][j];
            }
        }
        
        return f[now][n - 1];
    }
}

436. 最大正方形

中文

English

在一个二维01矩阵中找到全为1的最大正方形, 返回它的面积.

样例

样例 1:

输入:
[
  [1, 0, 1, 0, 0],
  [1, 0, 1, 1, 1],
  [1, 1, 1, 1, 1],
  [1, 0, 0, 1, 0]
]
输出: 4

样例 2:

输入: 
[
  [0, 0, 0],
  [1, 1, 1]
]
输出: 1

设定状态: dp[i][j] 表示以(i, j)为右下顶点的最大全1矩阵的边长.

状态转移方程:

if matrix[i][j] == 0
	dp[i][j] = 0
else                 // 此时为dp[i-1][j-1], dp[i-1][j], dp[i][j-1] 确定的区域的最大全1矩阵
	dp[i][j] = min{dp[i-1][j-1], dp[i-1][j], dp[i][j-1]} + 1	// 得到此方程需要一定推导, 纸笔画一下

边界: if i == 0 or j == 0: dp[i][j] = matrix[i][j]

答案: max{dp[i][j]}^2

class Solution:
    """
    @param grid: a matrix of 0 and 1
    @return: an integer
    """
    def maxSquare(self, grid):
        # write your code here
        row, col = len(grid), len(grid[0])
        dp = [[0]*col for i in range(row)]
        
        for i in range(0, row):
            dp[i][0] = grid[i][0]
        
        for j in range(0, col):
            dp[0][j] = grid[0][j]
        
        for i in range(1, row):
            for j in range(1, col):
                if grid[i][j]:
                    dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])+1
                else:
                    dp[i][j] = 0
        
        max_edge = max(max(dp[i]) for i in range(row))
        return max_edge*max_edge

 也可以利用滚动数组优化。

114. 不同的路径

中文

English

有一个机器人的位于一个 m × n 个网格左上角。

机器人每一时刻只能向下或者向右移动一步。机器人试图达到网格的右下角。

问有多少条不同的路径？

样例

Example 1:

Input: n = 1, m = 3
Output: 1	
Explanation: Only one path to target position.

Example 2:

Input:  n = 3, m = 3
Output: 6	
Explanation:
	D : Down
	R : Right
	1) DDRR
	2) DRDR
	3) DRRD
	4) RRDD
	5) RDRD
	6) RDDR

注意事项

n和m均不超过100
且答案保证在32位整数可表示范围内。

解法1:
数学模型：在n-1 + m-1长度的序列中，有n-1个D，和m-1个组成。
其中D表示向下，R表示向右。
因此满足组合数：C(n+m-2, n-1), 从n+m-2个位置中选n-1个位置放D的方案数。

解法2:
可以用Dp过程来求解：
Dp[i][j] 表示走到(i,j)的路径数，
考虑最后一步是从上往下走，还是从左往右走。
Dp[i][j] = Dp[i-1][j] + Dp[i][j-1];

class Solution:
    # @return an integer
    """
    def c(self, m, n):
        mp = {}
        for i in range(m):
            for j in range(n):
                if(i == 0 or j == 0):
                    mp[(i, j)] = 1
                else:
                    mp[(i, j)] = mp[(i - 1, j)] + mp[(i, j - 1)]
        return mp[(m - 1, n - 1)]

    def uniquePaths(self, m, n):
        return self.c(m, n)
    """
    
    def uniquePaths(self, m, n):
        dp = [[0]*n for i in range(m)]
        
        for i in range(m):
            dp[i][0] = 1    
            
        for j in range(n):
            dp[0][j] = 1
                
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
        
        return dp[m-1][n-1]

200. 最长回文子串

中文

English

给出一个字符串（假设长度最长为1000），求出它的最长回文子串，你可以假定只有一个满足条件的最长回文串。

样例

样例 1:

输入:"abcdzdcab"
输出:"cdzdc"

样例 2:

输入:"aba"
输出:"aba"

挑战

O(n²) 时间复杂度的算法是可以接受的，如果你能用 O(n) 的算法那自然更好。

class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        # write your code here
        start,end = 0,0
        n = len(s)

        def locatePalindrome(s, i, j):
            nonlocal start,end
            while i>=0 and j<n:
                if s[i] == s[j]:
                    if end-start < j-i+1:
                        start,end = i,j+1
                else:
                    break
                i -= 1
                j += 1
                
        for i in range(n):
            # center i
            locatePalindrome(s, i, i)
            # center i,i+1
            locatePalindrome(s, i, i+1)
        return s[start:end]            

            

 最常规的解法。

使用dp的：

我们首先初始化一字母和二字母的回文，然后找到所有三字母回文，并依此类推…

 注意为什么两个for一个递减一个递增？？？用二维矩阵画图说明，才不容易出错。

class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        # write your code here
        # dp[i][j] = dp[i+1][j-1] + (s[i]==s[j])  if i<j         
        n = len(s)
        dp = [[False]*n for i in range(n)]
        
        ans = s[0]
        for i in range(n):
            dp[i][i] = True
            if i < n-1 and s[i] == s[i+1]:
                dp[i][i+1] = True
                
        for i in range(n, -1, -1):
            for j in range(i+1, n):
                if i < n-1 and j > 0: 
                    if s[i] == s[j] and j != i+1:
                        dp[i][j] = dp[i+1][j-1]
        
        for i in range(n):
            for j in range(i+1, n):
                if dp[i][j] and len(ans) < (j-i+1):
                    ans = s[i:j+1]
        return ans
                                 

398. 最长上升连续子序列 II

中文

English

给定一个整数矩阵. 找出矩阵中的最长连续上升子序列, 返回它的长度.

最长连续上升子序列可以从任意位置开始, 向上/下/左/右移动.

样例

样例 1:

输入: 
    [
      [1, 2, 3, 4, 5],
      [16,17,24,23,6],
      [15,18,25,22,7],
      [14,19,20,21,8],
      [13,12,11,10,9]
    ]
输出: 25
解释: 1 -> 2 -> 3 -> 4 -> 5 -> ... -> 25 (由外向内螺旋)

样例 2:

输入: 
    [
      [1, 2],
      [5, 3]
    ]
输出: 5
解释: 1 -> 2 -> 3 -> 5

挑战

假定这是一个 N x M 的矩阵. 在 O(NM) 的时间复杂度和空间复杂度内解决这个问题.

• 动态规划的实现方式:
• 循环(从小到大递推)
• 记忆化搜索(从大到小搜索)

这个题目要用dfs+记忆化搜索比较方便。

分析:

• 多重循环DP遇到的困难:
• 到从上到下循环不能解决问题 • 初始状态不好定义

• 那我们有没有可以比较暴力解决的方法呢? • DFS

动态规划, 设定状态 f[i][j] 表示矩阵中坐标 (i, j) 的点开始的最长上升子序列

状态转移方程:

int dx[4] = {0, 1, -1, 0};
int dy[4] = {1, 0, 0, -1};

f[i][j] = max{ f[i + dx[k]][j + dy[k]] + 1 }

k = 0, 1, 2, 3, matrix[i + dx[k]][j + dy[k]] > matrix[i][j]

这道题目可以向四个方向走, 所以推荐使用记忆化搜索(递归)的写法. 本质上就是dfs+cache！！！

public class Solution {
    /**
     * @param matrix: A 2D-array of integers
     * @return: an integer
     */

    int[][] dp;
    int n, m;

    public int longestContinuousIncreasingSubsequence2(int[][] A) {
        if (A.length == 0) {
            return 0;
        }

        n = A.length;
        m = A[0].length;
        int ans = 0;
        dp = new int[n][m]; // dp[i][j] means the longest continuous increasing path from (i,j)
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                dp[i][j] = -1; // dp[i][j] has not been calculated yet
            }
        }

        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                search(i, j, A);
                ans = Math.max(ans, dp[i][j]);
            }
        }

        return ans;
    }

    int[] dx = { 1, -1, 0, 0 };
    int[] dy = { 0, 0, 1, -1 };

    void search(int x, int y, int[][] A) {
        if (dp[x][y] != -1) { // if dp[i][j] has been calculated, return directly
            return;
        }

        int nx, ny;
        dp[x][y] = 1;
        for (int i = 0; i < 4; ++i) {
            nx = x + dx[i];
            ny = y + dy[i];
            if (nx >= 0 && nx < n && ny >= 0 && ny < m) {
                if (A[nx][ny] > A[x][y]) {
                    search(nx, ny, A); // dp[nx][ny] must be calcuted
                    dp[x][y] = Math.max(dp[x][y], dp[nx][ny] + 1);
                }
            }
        }
    }
}

什么时候用记忆化搜索? 1. 状态转移特别麻烦，不是顺序性

2. 初始化状态不是很容易找到

记忆化搜索的缺陷

耗费更多空间，无法使用滚动数组优化 递归深度可能会很深

博弈类动态规划 Game DP

394. 硬币排成线

中文

English

有 n 个硬币排成一条线。两个参赛者轮流从右边依次拿走 1 或 2 个硬币，直到没有硬币为止。拿到最后一枚硬币的人获胜。

请判定 先手玩家 必胜还是必败?

若必胜, 返回 true, 否则返回 false.

样例

样例 1:

输入: 1
输出: true

样例 2:

输入: 4
输出: true
解释: 
先手玩家第一轮拿走一个硬币, 此时还剩三个.
这时无论后手玩家拿一个还是两个, 下一次先手玩家都可以把剩下的硬币拿完.

挑战

O(1) 时间复杂度且O(1) 存储。

分析

• 面对N个石子，先手Alice第一步可以拿1个或2个石子

• 这样后手Bob就面对N-1个石子或N-2个石子

• 先手Alice一定会选择能让自己赢的一步 – 因为双方都是采取最优策略

• 怎么选择让自己赢的一步
• 就是走了这一步之后，对手面对剩下的石子，他必输

分析

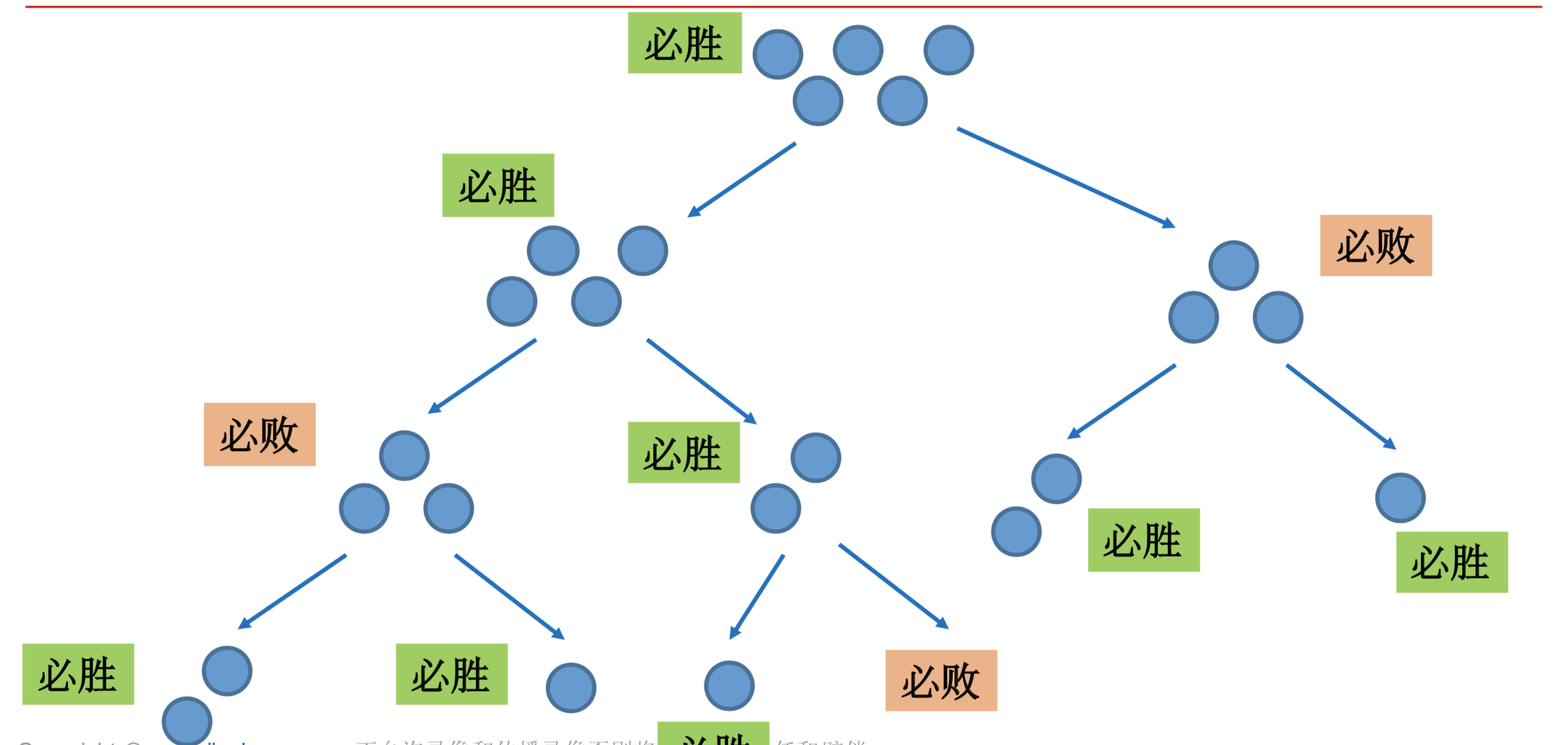
• 状态:设f[i]表示面对i个石子，是否先手必胜(f[i] = TRUE / FALSE)

• 转移方程:f[i] = f[i-1] == FALSE OR f[i-2] == FALSE

• 初始条件和边界情况:
– f[0] = FALSE --- 面对0个石子，先手必败
– f[1] = f[2] = TRUE --- 面对1个石子或2个石子，先手必胜

• 计算顺序:f[0], f[1], f[2], ..., f[N]
• 如果f[N] = TRUE则先手必胜，否则先手必败

• 时间复杂度O(N)，空间复杂度O(N)，可以滚动数组优化至O(1)

 

代码省去。另外，

可以证明, 当硬币数目是3的倍数的时候, 先手玩家必败, 否则他必胜.

当硬币数目是3的倍数时, 每一轮先手者拿a个, 后手者拿3-a个即可, 后手必胜.

若不是3的倍数, 先手者可以拿1或2个, 此时剩余硬币个数就变成了3的倍数.

395. 硬币排成线 II

中文

English

有 n 个不同价值的硬币排成一条线。两个参赛者轮流从 左边 依次拿走 1 或 2 个硬币，直到没有硬币为止。计算两个人分别拿到的硬币总价值，价值高的人获胜。

请判定 先手玩家 必胜还是必败?

若必胜, 返回 true, 否则返回 false.

样例

样例 1:

输入: [1, 2, 2]
输出: true
解释: 先手玩家直接拿走两颗硬币即可.

样例 2:

输入: [1, 2, 4]
输出: false
解释: 无论先手拿一个还是两个, 后手可以拿完, 然后总价值更高.

动态规划, 设定状态 f[i] 表示剩余 i, i+1, ..., n-1 这些硬币时, 先手者可以拿到的最大价值.

设 sum[i] = values[i] + values[i+1] + ... + values[n-1].

此时后手者拿到的价值即为 sum[i] - f[i].

在这个状态设定下, 答案即为 f[0] > sum[0] - f[0].

状态转移方程为:

f[i] = max(
    sum[i+1] - f[i+1] + values[i],                  // 先手者拿一枚
    sum[i+2] - f[i+2] + values[i] + values[i+1]	    // 先手者拿两枚
);

观察到每次计算只涉及 i+1 和 i+2 的状态, 因此可以将空间优化到O(1).

class Solution:
    # @param values: a list of integers
    # @return: a boolean which equals to True if the first player will win
    def firstWillWin(self, values):
        # write your code here
        n, total = len(values), sum(values)
        sumv, f = [], []
        
        if n<3: 
            return True
            
        # prefix sum
        for i in range(n):
            sumv.append(total)
            total -= values[i]
            
        f.append(sumv[n-1])
        f.append(sumv[n-2])
        
        for i in range(n-3, -1, -1):
            f.append(max(values[i]+(sumv[i+1]-f[n-1-i-1]), values[i]+values[i+1]+(sumv[i+2]-f[n-1-i-2])))
        
        if f[n-1] < sumv[0]-f[n-1]: 
            return False
            
        else: return True

区间类DP

特点:
1. 求一段区间的解max/min/count 2. 转移方程通过区间更新
3. 大区间的值依赖于小区间

168. 吹气球

中文

English

有n个气球，编号为0到n-1，每个气球都有一个分数，存在nums数组中。每次吹气球i可以得到的分数为 nums[left] * nums[i] * nums[right]，left和right分别表示i气球相邻的两个气球。当i气球被吹爆后，其左右两气球即为相邻。要求吹爆所有气球，得到最多的分数。

样例

样例 1:

输入：[4, 1, 5, 10]
输出：270
解释：
nums = [4, 1, 5, 10] 吹爆 1, 得分 4 * 1 * 5 = 20
nums = [4, 5, 10]   吹爆 5, 得分 4 * 5 * 10 = 200 
nums = [4, 10]   吹爆 4, 得分 1 * 4 * 10 = 40
nums = [10]   吹爆 10, 得分 1 * 10 * 1 = 10
总得分 20 + 200 + 40 + 10 = 270

样例 2:

输入：[3,1,5]
输出：35
解释：
nums = [3, 1, 5] 吹爆 1, 得分 3 * 1 * 5 = 15
nums = [3, 5] 吹爆 3, 得分 1 * 3 * 5 = 15
nums = [5] 吹爆 5, 得分 1 * 5 * 1 = 5
总得分 15 + 15 + 5  = 35

注意事项

1. 你可以假设nums[-1] = nums[n] = 1。-1和n位置上的气球不真实存在，因此不能吹爆它们。
2. 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

 

反正坑比较多，要推导出来完全写对还是有难度。

396. 硬币排成线 III

中文

English

有 n 个硬币排成一条线, 第 i 枚硬币的价值为 values[i].

两个参赛者轮流从任意一边取一枚硬币, 直到没有硬币为止. 拿到硬币总价值更高的获胜.

请判定 第一个玩家 会赢还是会输.

样例

样例 1:

输入: [3, 2, 2]
输出: true
解释: 第一个玩家在刚开始的时候拿走 3, 然后两个人分别拿到一枚 2.

样例 2:

输入: [1, 20, 4]
输出: false
解释: 无论第一个玩家在第一轮拿走 1 还是 4, 第二个玩家都可以拿到 20.

挑战

在 n 是偶数时做到O(1) 空间, O(n) 时间

区间动态规划问题, 具体定义状态的方式有很多种, 但是大同小异, 时空复杂度都相似. 这里只介绍 version 1 的具体实现.

设定 dp[i][j] 表示当前剩余硬币的区间为 [i, j] 时, 此时该拿硬币的人能获取的最大值.

注意, dp[i][j] 并没有包含角色信息, dp[0][values.length - 1] 表示的是先手的人能获得的最大值, 而 dp[1][values.length -1] 表示的则是后手的人能获得的最大值. 需要这样做是因为: 两个人都会采用最优策略.

当前的人的决策就是拿左边还是拿右边, 而下一个人仍然会最优决策, 所以应该是最小值中取最大值:

dp[i][j] = max(	                                     // 取max表示当前的人选用最优策略		
    min(dp[i + 2][j], dp[i + 1][j - 1]) + values[i], // 取min表示下一个人选用最优策略
    min(dp[i][j - 2], dp[i + 1][j - 1]) + values[j]
)

几个边界:

i > j : dp[i][j] = 0
i == j : dp[i][j] = values[i]
i + 1 == j : dp[i][j] = max(values[i], values[j])

class Solution:
    # @param values: a list of integers
    # @return: a boolean which equals to True if the first player will win
    def firstWillWin(self, values):
        if not values:
            return False
            
        n = len(values)
        dp = [[0] * n for _  in range(n)]
        sum = [[0] * n for _  in range(n)]
        
        for i in range(n):
            dp[i][i] = values[i]
            sum[i][i] = values[i]
        
        for i in range(n - 2, -1, -1):  # n-2 => 0
            for j in range(i + 1, n):  # i+1 => n-1
                sum[i][j] = sum[i + 1][j] + values[i]
                dp[i][j] = sum[i][j] - min(dp[i + 1][j], dp[i][j - 1])
                
        return dp[0][n - 1] > sum[0][n - 1] - dp[0][n - 1]

区间类的动态规划还是挺难的！！！看情况掌握吧。

 

双序列动态规划

77. 最长公共子序列

中文

English

给出两个字符串，找到最长公共子序列(LCS)，返回LCS的长度。

样例

样例 1:
	输入:  "ABCD" and "EDCA"
	输出:  1
	
	解释:
	LCS 是 'A' 或  'D' 或 'C'


样例 2:
	输入: "ABCD" and "EACB"
	输出:  2
	
	解释: 
	LCS 是 "AC"

说明

最长公共子序列的定义：

• 最长公共子序列问题是在一组序列（通常2个）中找到最长公共子序列（注意：不同于子串，LCS不需要是连续的子串）。该问题是典型的计算机科学问题，是文件差异比较程序的基础，在生物信息学中也有所应用。
  
• https://en.wikipedia.org/wiki/Longest_common_subsequence_problem

class Solution:
    """
    @param A: A string
    @param B: A string
    @return: The length of longest common subsequence of A and B
    """
    def longestCommonSubsequence(self, A, B):
        # write your code here
        if not A or not B:
            return 0
            
        m, n = len(A), len(B)
        dp = [[0]*n for i in range(m)]
        
        for i in range(0, m):
            if A[i] == B[0]:
                dp[i][0] = 1
        
        for j in range(0, n):
            if A[0] == B[j]:
                dp[0][j] = 1
        
        for i in range(1, m):
            for j in range(1, n):
                if A[i] == B[j]:
                    dp[i][j] = max(dp[i-1][j-1]+1, dp[i][j-1], dp[i-1][j])
                else:
                    dp[i][j] = max(dp[i][j-1], dp[i-1][j])
        
        return dp[m-1][n-1]
        

 记得画个二维的图！！！

Dp[i][j] 表示A序列前i个数，与B的前j个数的LCS长度。
对A的每个位置i，枚举B的每个位置j。

更精简的代码：

class Solution:
    """
    @param A, B: Two strings.
    @return: The length of longest common subsequence of A and B.
    """
    def longestCommonSubsequence(self, A, B):
        n, m = len(A), len(B)
        f = [[0] * (n + 1) for i in range(m + 1)]
        for i in range(n):
            for j in range(m):
                f[i + 1][j + 1] = max(f[i][j + 1], f[i + 1][j])
                if A[i] == B[j]:
                    f[i + 1][j + 1] = f[i][j] + 1
        return f[n][m]

备注：也可以使用滚动数组进行优化！！！

119. 编辑距离

中文

English

给出两个单词word1和word2，计算出将word1 转换为word2的最少操作次数。

你总共三种操作方法：

• 插入一个字符
• 删除一个字符
• 替换一个字符
  

样例

样例 1:

输入: 
"horse"
"ros"
输出: 3
解释: 
horse -> rorse (替换 'h' 为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

样例 2:

输入: 
"intention"
"execution"
输出: 5
解释: 
intention -> inention (删除 't')
inention -> enention (替换 'i' 为 'e')
enention -> exention (替换 'n' 为 'x')
exention -> exection (替换 'n' 为 'c')
exection -> execution (插入 'u')

class Solution:
    """
    @param A: A string
    @param B: A string
    @return: The minimum number of steps.
    """
    def minDistance(self, A, B):
        # write your code here
        m, n = len(A), len(B)
        dp = [[0]*(n+1) for i in range(m+1)]
        
        for i in range(m+1):
            dp[i][0] = i
            
        for j in range(n+1):
            dp[0][j] = j
        
        for i in range(1, m+1):
            for j in range(1, n+1):
                if A[i-1] == B[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j])+1
        
        return dp[m][n]

dp[i][j] 代表第一个字符串以i结尾匹配上（编辑成）第二个字符串以j结尾的字符串，最少需要多少次编辑。
通过去判断i与j的匹配关系来变为更小的状态。

字符串相似性！！！

29. 交叉字符串

中文

English

给出三个字符串:s1、s2、s3，判断s3是否由s1和s2交叉构成。

样例

样例 1：

输入:
"aabcc"
"dbbca"
"aadbbcbcac"
输出:
true

样例 2：

输入:
""
""
"1"
输出:
false

样例 3：

输入:
"aabcc"
"dbbca"
"aadbbbaccc"
输出:
false

挑战

要求时间复杂度为O(n²)或者更好

class Solution:
    """
    @param A: A string
    @param B: A string
    @param C: A string
    @return: Determine whether s3 is formed by interleaving of s1 and s2
    """
    def isInterleave(self, A, B, C):
        # write your code here
        m, n = len(A), len(B)
        
        if m + n != len(C):
            return False
            
        dp = [[False]*(n+1) for i in range(m+1)]
        
        dp[0][0] = True
        
        for i in range(1, m+1):
            if A[i-1] == C[i-1]:
                dp[i][0] = dp[i-1][0]
            
        for j in range(1, n+1):
            if B[j-1] == C[j-1]:
                dp[0][j] = dp[0][j-1]
        
        for i in range(1, m+1):
            for j in range(1, n+1):
                if A[i-1] == C[i+j-1]:
                    dp[i][j] = dp[i-1][j]
                if B[j-1] == C[i+j-1]:
                    dp[i][j] |= dp[i][j-1]
                
        return dp[m][n]
        
        

 dp[i][j]代表由s1的前i个字母和s2的前j个字母是否能构成当前i+j个字母。
然后状态转移即可。（看第i+j+1个是否能被s1的第i+1个构成或被s2的第j+1个构成）

623. K步编辑

中文

English

给出一个只含有小写字母的字符串的集合以及一个目标串，输出所有可以经过不多于 k 次操作得到目标字符串的字符串。

你可以对字符串进行一下的3种操作:

• 加入1个字母

• 删除1个字母

• 替换1个字母

样例

样例 1:

给出字符串 `["abc","abd","abcd","adc"]`，目标字符串为 `"ac"` ，k = `1`
返回 `["abc","adc"]`
输入:
["abc", "abd", "abcd", "adc"]
"ac"
1
输出:
["abc","adc"]

解释:
"abc" 去掉 "b"
"adc" 去掉 "d"

样例 2:

输入:
["acc","abcd","ade","abbcd"]
"abc"
2
输出:
["acc","abcd","ade","abbcd"]

解释:
"acc" 把 "c" 变成 "b"
"abcd" 去掉 "d"
"ade" 把 "d" 变成 "b"把 "e" 变成 "c"
"abbcd" 去掉 "b" 和 "d"

class TrieNode:
    def __init__(self):
        # Initialize your data structure here.
        self.children = [None for i in range(26)]
        self.hasWord = False
        self.str = None
    
    @classmethod
    def addWord(cls, root, word):
        node = root
        for letter in word:
            child = node.children[ord(letter) - ord('a')]
            if child is None:
                child = TrieNode()
                node.children[ord(letter) - ord('a')] = child
            node = child
    
        node.hasWord = True
        node.str = word

class Solution:
    # @param {string[]} words a set of strings
    # @param {string} target a target string
    # @param {int} k an integer
    # @return {string[]} output all the stirngs that meet the requirements 
    def kDistance(self, words, target, k):
        # Write your code here
        root = TrieNode()
        for word in words:
            TrieNode.addWord(root, word)

        result = []
        n = len(target)
        dp = [i for i in range(n + 1)]

        self.find(root, result, k, target, dp)
        return result

    def find(self, node, result, k, target, dp):
        n = len(target)

        if node.hasWord and dp[n] <= k:
            result.append(node.str)

        next = [0 for i in range(n + 1)]

        for i in range(26):
            if node.children[i] is not None:
                next[0] = dp[0] + 1
                for j in range(1, n + 1):
                    if ord(target[j - 1]) - ord('a') == i:
                        next[j] = min(dp[j - 1], min(next[j - 1] + 1, dp[j] + 1))
                    else:
                        next[j] = min(dp[j - 1] + 1, min(next[j - 1] + 1, dp[j] + 1))

                self.find(node.children[i], result, k, target, next)

 挺难的题目，使用了Trie，结合DP。

背包类DP

92. 背包问题

中文

English

在n个物品中挑选若干物品装入背包，最多能装多满？假设背包的大小为m，每个物品的大小为A[i]

样例

样例 1:
	输入:  [3,4,8,5], backpack size=10
	输出:  9

样例 2:
	输入:  [2,3,5,7], backpack size=12
	输出:  12
	

挑战

O(n x m) time and O(m) memory.

O(n x m) memory is also acceptable if you do not know how to optimize memory.

注意事项

你不可以将物品进行切割。

class Solution:
    """
    @param m: An integer m denotes the size of a backpack
    @param A: Given n items with size A[i]
    @return: The maximum size
    """
    def backPack(self, m, A):
        # write your code here
        # f[i][j]表示前i个物品选一些物品放入容量为j的背包中能否放满。
        n = len(A)
        f = [[False] * (m + 1) for _ in range(n + 1)]
        
        f[0][0] = True
        for i in range(1, n + 1):
            f[i][0] = True
            for j in range(1, m + 1):
                if j >= A[i - 1]:
                    f[i][j] = f[i - 1][j] or f[i - 1][j - A[i - 1]]
                else:
                    f[i][j] = f[i - 1][j]
                    
        for i in range(m, -1, -1):
            if f[n][i]:
                return i
        return 0
            
        
        

 

自己画一个二维的矩阵图，推演下。

125. 背包问题 II

中文

English

有 n 个物品和一个大小为 m 的背包. 给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值.

问最多能装入背包的总价值是多大?

样例

样例 1:

输入: m = 10, A = [2, 3, 5, 7], V = [1, 5, 2, 4]
输出: 9
解释: 装入 A[1] 和 A[3] 可以得到最大价值, V[1] + V[3] = 9 

样例 2:

输入: m = 10, A = [2, 3, 8], V = [2, 5, 8]
输出: 10
解释: 装入 A[0] 和 A[2] 可以得到最大价值, V[0] + V[2] = 10

挑战

O(nm) 空间复杂度可以通过, 不过你可以尝试 O(m) 空间复杂度吗?

注意事项

1. A[i], V[i], n, m 均为整数
2. 你不能将物品进行切分
3. 你所挑选的要装入背包的物品的总大小不能超过 m
4. 每个物品只能取一次

设定 f[i][j] 表示前 i 个物品装入大小为 j 的背包里, 可以获取的最大价值总和. 决策就是第i个物品装不装入背包, 所以状态转移方程就是 f[i][j] = max(f[i - 1][j], f[i - 1][j - A[i]] + V[i])

class Solution:
    # @param m: An integer m denotes the size of a backpack
    # @param A & V: Given n items with size A[i] and value V[i]
    def backPackII(self, m, A, V):
        # write your code here
        f = [0 for i in range(m+1)]
        n = len(A)
        for i in range(n):
            for j in range(m, A[i]-1, -1):
                f[j] = max(f[j] , f[j-A[i]] + V[i])
        return f[m]

440. 背包问题 III

中文

English

给定 n 种物品, 每种物品都有无限个. 第 i 个物品的体积为 A[i], 价值为 V[i].

再给定一个容量为 m 的背包. 问可以装入背包的最大价值是多少?

样例

样例 1:

输入: A = [2, 3, 5, 7], V = [1, 5, 2, 4], m = 10
输出: 15
解释: 装入三个物品 1 (A[1] = 3, V[1] = 5), 总价值 15.

样例 2:

输入: A = [1, 2, 3], V = [1, 2, 3], m = 5
输出: 5
解释: 策略不唯一. 比如, 装入五个物品 0 (A[0] = 1, V[0] = 1).

注意事项

1. 不能将一个物品分成小块.
2. 放入背包的物品的总大小不能超过 m.

class Solution:
    # @param {int[]} A an integer array
    # @param {int[]} V an integer array
    # @param {int} m an integer
    # @return {int} an array
    def backPackIII(self, A, V, m):
        # Write your code here
        f = [0 for i in range(m+1)]
        for (a, v) in zip(A, V):
            for j in range(a, m+1):
                if f[j - a] + v > f[j]:
                    f[j] = f[j - a] + v
        return f[m]