数据预处理
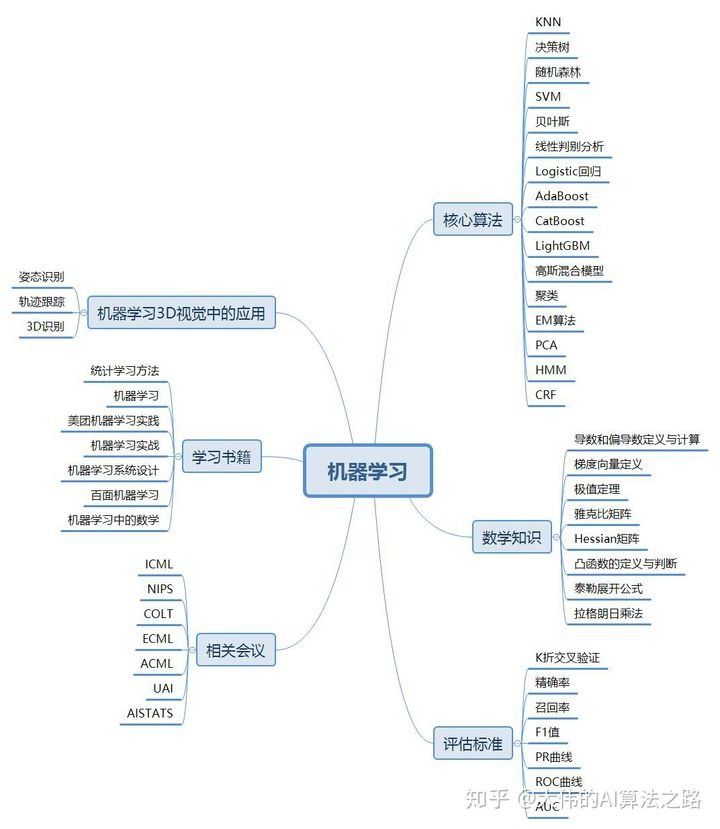
1、深度学习中的数据预处理有哪些方式?
1、 数据归一化。包括高斯归一化、最大最小值归一化等。
2、 白化。许多深度学习算法都依赖于白化来获得更好的特征。所谓的白化,以PCA白化来说,就是对PCA降维后的数据的每一列除以其特征值的根号。
2、为什么需要对数据进行归一化处理,归一化的方式有哪些?
1. 为了后面数据处理的方便,归一化的确可以避免一些不必要的数值问题。
2. 为了程序运行时收敛加快。(如果)
3. 同一量纲。样本数据的评价标准不一样,需要对其量纲化,统一评价标准。这算是应用层面的需求。
4. 避免神经元饱和。啥意思?就是当神经元的激活在接近 0 或者 1 时会饱和,在这些区域,梯度几乎为 0,这样,在反向传播过程中,局部梯度就会接近 0,这会有效地“杀死”梯度。
5. 保证输出数据中数值小的不被吞食。
详细请参考:https://blog.csdn.net/code_lr/article/details/51438649
归一化的方式主要有:线性归一化、标准差归一化、非线性归一化
线性归一化:
标准差归一化:
非线性归一化:
适用范围为:经常用在数据分化比较大的场景,有些数值很大,有些很小。通过一些数学函数,将原始值进行映射。该方法包括指数,正切等。
3、数据增强的方式有哪些?
翻转、旋转、缩放、裁剪、平移、尺度变换、添加噪声、色彩抖动、亮度调整、对比度增强。
注意:在数据量比较少的情况下,数据增强的方式对模型效果的提升(泛化能力)很有效。
数据增强可以分为两类,一类是离线增强,一类是在线增强。
离线增强:直接对数据集进行处理,数据的数目会变成增强因子乘以原数据集的数目,这种方法常常用于数据集很小的时候。
在线增强:这种增强的方法用于,获得 batch 数据之后,然后对这个 batch 的数据进行增强,如旋转、平移、翻折等相应的变化,由于有些数据集不能接受线性级别的增长,这种方法长用于大的数据集,很多机器学习框架已经支持了这种数据增强方式,并且可以使用 GPU 优化计算。
物体检测中的数据增强:其实和正常的数据增强一样的,数据本身增强后,对box进行一定的平移旋转即可。
4、深度学习如何解决数据样本不均衡?你在项目中是怎么解决的?
1、数据增强
2、使用Focal loss
深度学习中的名词解释
1、奥卡姆剃刀的思想?
在所有可能选择的模型中,我们应该选择能够很好地解释已知数据并且十分简单的模型。
换句话说,同等效果下,选择较为简单的模型。
奥卡姆剃刀思想用在哪里呢?其实就是深度学习中的正则化。
2、梯度消失和梯度爆炸?
两种情况下梯度消失经常出现,一是在深层网络中,二是采用了不合适的损失函数,比如sigmoid。
梯度爆炸一般出现在深层网络和权值初始化值太大的情况下。
由链式法则可知,当采用sigmoid这类函数时,深层网络参数更新时,往往会出现梯度消失现象。当初始参数大时,也会出现梯度爆炸。
详细请参考:https://blog.csdn.net/qq_25737169/article/details/78847691
3、鞍点、局部最小值和全局最小值?如何区分它们?如何跳出鞍点和局部最小值?
鞍点和局部极小值、全局最小值的梯度都相等,均为0,不同在于在鞍点附近Hessian矩阵是不定的(行列式小于0,行列式必须是方阵),而在局部极小值附件的Hessian矩阵是正定的。
关于正定矩阵,是特征值都不小于0的实对称矩阵,关于负定矩阵是特征值都小于0的实对称矩阵,关于不定矩阵是特征值既有大于0又有小于0的值。
跳出鞍点或者局部最小点一般有以下几种方式:
1、 以多组不同参数值初始化多个神经网络,按标准方法训练后,取其中误差最小的解作为最终参数。这相当于从多个不同的初始点开始搜索,这样就可能陷入不同的局部极小,从中进行选择有可能获得更接近全局最小的结果。
2、 使用“模拟退火”技术。模拟退火在每一步都以一定的概率接受比当前解更差的结果,从而有助于“跳出”局部极小。在每步迭代过程中,接受“次优解”的概率要随着时间的推移而逐渐降低,从而保证算法稳定。
3、 使用随机梯度下降,与标准梯度下降法精确计算梯度不同,随机梯度下降法在计算梯度时加入了随机因素。于是,即便现如局部极小点,它计算出的梯度仍可能不为零,这样就有机会跳出局部极小继续搜索。
4、深度学习中的超参数有哪些?
超参数 : 在机器学习的上下文中,超参数是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。通常情况下,需要对超参数进行优化,给学习机选择一组最优超参数,以提高学习的性能和效果。
超参数指的是会影响到最终参数的参数,主要包括卷积核大小和数量、是否采用BN和池化操作、迁移学习、参数的初始化方式、学习率、损失函数、激活函数、是否采用自适应学习率、优化器的选择等等。
5、如何寻找超参数的最优值?
在使用机器学习算法时,总有一些难调的超参数。例如权重衰减大小,高斯核宽度等等。这些参数需要人为设置,设置的值对结果产生较大影响。常见设置超参数的方法有:
1. 猜测和检查:根据经验或直觉,选择参数,一直迭代。
2. 网格搜索:让计算机尝试在一定范围内均匀分布的一组值。
3. 随机搜索:让计算机随机挑选一组值。
4. 贝叶斯优化:使用贝叶斯优化超参数,会遇到贝叶斯优化算法本身就需要很多的参数的困难。
5. MITIE方法,好初始猜测的前提下进行局部优化。它使用BOBYQA算法,并有一个精心选择的起始点。由于BOBYQA只寻找最近的局部最优解,所以这个方法是否成功很大程度上取决于是否有一个好的起点。在MITIE的情况下,我们知道一个好的起点,但这不是一个普遍的解决方案,因为通常你不会知道好的起点在哪里。从好的方面来说,这种方法非常适合寻找局部最优解。稍后我会再讨论这一点。
6. 最新提出的LIPO的全局优化方法。这个方法没有参数,而且经验证比随机搜索方法好。
6、训练集、验证集、测试集和交叉验证
一般来说,训练集、验证集、测试集对中型数据来说,一般划分的比例为6:2:2,但是对于特别大的数据集,比如100w的级别,这个时候,完全没有必要再按照6:2:2的方式,可以加大训练量,使模型得到更充足的训练,此时可以调整为8:1:1的比例,甚至给验证集和测试集更小的比例。
K折交叉验证:把数据分成K份,每次拿出一份作为验证集,剩下k-1份作为训练集,重复K次。最后平均K次的结果,作为误差评估的结果。与前两种方法对比,只需要计算k次,大大减小算法复杂度,被广泛应用。一般情况将K折交叉验证用于模型调优,找到使得模型泛化性能最优的超参值。找到后,在全部训练集上重新训练模型,并使用独立测试集对模型性能做出最终评价。
如果训练数据集相对较小,则增大k值。
增大k值,在每次迭代过程中将会有更多的数据用于模型训练,能够得到最小偏差,同时算法时间延长。且训练块间高度相似,导致评价结果方差较高。
如果训练集相对较大,则减小k值。
减小k值,降低模型在不同的数据块上进行重复拟合的性能评估的计算成本,在平均性能的基础上获得模型的准确评估。
7、线性分类器的三个最佳准则
感知准则函数、支持向量机、Fisher准则。
8、KL散度和JS散度
KL散度又称之为KL距离,相对熵:
当P(X)和Q(X)的相似度越高,KL散度越小。
KL散度主要有两个性质:
(1) 不对称性
尽管KL散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即
(2) 非负性
相对熵的值是非负值,即
JS散度
JS散度也称JS距离,是KL散度的一种变形。
转自:https://www.zhihu.com/people/18301926762/posts?page=14
https://zhuanlan.zhihu.com/p/97311641