995. Minimum Number of K Consecutive Bit Flips
In an array A containing only 0s and 1s, a K-bit flip consists of choosing a (contiguous) subarray of length K and simultaneously changing every 0 in the subarray to 1, and every 1 in the subarray to 0.
Return the minimum number of K-bit flips required so that there is no 0 in the array. If it is not possible, return -1.
Example 1:
Input: A = [0,1,0], K = 1
Output: 2
Explanation: Flip A[0], then flip A[2].
Example 2:
Input: A = [1,1,0], K = 2
Output: -1
Explanation: No matter how we flip subarrays of size 2, we can't make the array become [1,1,1].
Example 3:
Input: A = [0,0,0,1,0,1,1,0], K = 3
Output: 3
Explanation:
Flip A[0],A[1],A[2]: A becomes [1,1,1,1,0,1,1,0]
Flip A[4],A[5],A[6]: A becomes [1,1,1,1,1,0,0,0]
Flip A[5],A[6],A[7]: A becomes [1,1,1,1,1,1,1,1]
Note:
1 <= A.length <= 30000
1 <= K <= A.length
题目大意:题目要求将窗口K内的所有数字反转,0变1,1变0,最后要求整个数组不存在0,问最低反转多少次。
思路:看到题时一直在想:最低反转多少次?用dp?好像怎么也推不出转移公式,因为前面有0就必须反转,不存在需不需要反转的问题。用greedy? 看了下标签果然,贪心+滑动窗口。
基本思路是:遇到0即反转以当前位置起始的窗口K内的所有位置,但如果每次都修改数组里的值,时间复杂度会变为K*N,那有没有办法将时间复杂度降为N呢?答案是有!用变量cur记录当前位曾反转的次数,可以得出结论,只有前面K-1个位置会影响当前位置的反转次数,因此用cur记录前面K-1个位置的反转次数和。是不是很耳熟?窗口加和啊,后面加一个前面减一个啊,减神马呢?用一个与输入等长的数组flip记录每位数字是否需要反转,用变量res记录最终反转多少次。
用例子来说明:[0,0,0,1,0,1,1,0], K=3
注:每次计算i位时,为以i为起始长度为K的窗口,图中标黄色的长度为K的窗口为对当前位有反转影响的窗口(比如看一个数组前四位,A = [A[0], A[1], A[2], A[3]....], k=3. 看 A[3]的位置。A[3]的位置只跟A[1], A[2]有关系,如果A[1]要反,肯定要反1,2,3,如果A[2]要反,肯定要反2,3,4。但如果A[0]反,就只反0,1,2,对A[3]没有影响)。比如第五步判断i=3时,计算窗口i=3,4,5位是否需要被反转, 而对3,4,5位是否需要被反转结果有影响的窗口为第五步图中标黄的窗口i=1,2,3.
第一步:初始化 cur = 0, res = 0, flip = 0

第二步:判断i=0时,此时cur为初始值0,并且i <K未达到窗口长度,因此cur即为当前数字曾经反转的次数,cur % 2 == 0(即相当于未曾被反转过)。A[0] = 0,题目要求不存在0,因此i=0位需要被反转。
更新cur = 1, res = 1, flip[0] = 1;此时窗口长度为1.

第三步:判断i=1时,此时cur = 1, i<K未达到窗口长度,cur为当前数字曾经反转的次数,cur % 2 = 1(即当前数字已被反转过,而且未被反转回来,即1->0, 0->1),A[1] = 0,因此此时 i=1位已经被反转为1,不需要再进行操作。当前窗口长度为2.

第四步:与第三步同,窗口长度为3==K

第五步:判断i=3时,当前cur=1, 因为滑到i=3时窗口长度为4>K,第i-K=0位的反转不会影响到i=3的位置,只有i =1,2位的反转操作窗口包含了i=3位。因此cur需要减掉对第i-K位的反转次数才能得到当前位曾经被反转的次数。因此cur = cur -flip[i-K] = 1-1=0. 即i=3位未被反转过(it make sense, 因为以i=1, i=2位起始的窗口都未作反转操作)。但A[3] = 1已经是1了,因此还是不需要进行操作,只需要更新cur值:
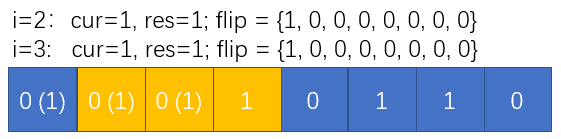
第六步:判断i=4时,cur = 0, cur = cur-flip[i-K] = 0-0=0, 当前值未被反转过,且A[4] = 0,因此需要进行反转操作,更新cur = cur+1=1, res = res+1=2, flip[4] = 1:

第七步:判断i=5时,cur = 1, cur = cur - flip[i-K] =1-0=1, cur % 2 = 1即当前值已经被反转(0->1, 1->0),且A[5] = 1, 说明A[5]经过前面的反转已经变为0了,因此需要再次被反转成为1.
更新cur = cur+1=2, res = res+1=3, flip[5] = 1:
注:因为此时i+K = A.size(),因此以i=5起始的窗口为最后一个窗口,其后的窗口都小于K. 因此也是反转操作的最后一个窗口。

第七步:判断i=6, cur = 2, cur = cur-flip[i-K] = 2-0=2, cur % 2 = 0,即当前值虽然曾经被反转过,但反转过偶数次,即经过前面窗口内值的反转后值不变。A[6] = 1:
注:因为i +K=6+3 >A.size(),因此此位不管是0是1都不能进行反转操作,为1即可向后判断,为0则直接返回-1.

第八步:判断i=7, cur = 2, cur = cur-flip[i-K] = 2-1 = 1, cur % 2 = 1, 即当前值已被反转为不同的值(0->1, 1->0), A[7] = 0,经反转后变为1

第九步:返回res值。代码如下:
1 class Solution { 2 public: 3 int minKBitFlips(vector<int>& A, int K) { 4 int res = 0, cur = 0; 5 vector<int> flip(A.size(), 0); 6 for(int i=0; i<A.size(); i++){ 7 if(i >= K) cur -= flip[i-K]; 8 if((A[i] == 0 && cur % 2 == 0) || 9 (A[i] == 1 && cur % 2 == 1)){ 10 if(i > A.size()-K){ 11 return -1; 12 } else { 13 res++; 14 cur++; 15 flip[i] = 1; 16 } 17 } 18 } 19 return res; 20 } 21 };
画图太痛苦了~画的我想吐血