题目链接:http://hihocoder.com/problemset/problem/1048
题目大意:用1*2或者2*1的方块铺满一个N*M的大方格,共有多少种方法。结果对1e9+7取余。2<=N<=1000, 3<=m<=5
解题思路:挑战程序设计竞赛上有基本上一样的题目,可以参考,原题中也有提示。大致思路就是,如果从左往右铺的话,那么对第i行j列的方块来说,第i-1行的方块一定全部铺过,第j+2行的一定没有铺过。所以我们可以保存第i行和第i+1行的状态,然后递推。又由于m<=5,所以可以将两行的状态压缩成整数。具体递推过程:
1 int t = 0; 2 //位置(i, j)已经被铺 3 if(s1 & (1 << k)){ 4 if(j < m) t = dp[i][j + 1][s1][s2]; //由下一个方块递推 5 else if(i < n) t = dp[i + 1][1][s2][0]; //从下一行第一个递推 6 else t = 0; 7 } 8 else{ 9 if(j < m && !(s1 & (1 << (k - 1)))) //可以横着铺 10 t += dp[i][j][s1 | (1 << k - 1) | (1 << k)][s2]; 11 t %= mod; 12 if(i < n && !(s2 & (1 << k))) //可以竖着铺 13 t += dp[i][j][s1 | (1 << k)][s2 | (1 << k)]; 14 t %= mod; 15 } 16 dp[i][j][s1][s2] += t % mod;
完整代码:
1 const int maxn = 1e3 + 5; 2 int n, m; 3 int dp[maxn][6][35][35]; 4 5 void solve(){ 6 memset(dp, 0, sizeof(dp)); 7 for(int s2 = (1 << m) - 1; s2 >= 0; s2--) dp[n][m][(1 << m) - 1][s2] = 1; 8 for(int i = n; i >= 1; i--){ 9 for(int j = m; j >= 1; j--){ 10 int k = m - j; 11 for(int s1 = (1 << m) - 1; s1 >= 0; s1--){ 12 for(int s2 = (1 << m) - 1; s2 >= 0; s2--){ 13 int t = 0; 14 //位置(i, j)已经被铺 15 if(s1 & (1 << k)){ 16 if(j < m) t = dp[i][j + 1][s1][s2]; //由下一个方块递推 17 else if(i < n) t = dp[i + 1][1][s2][0]; //从下一行第一个递推 18 else t = 0; 19 } 20 else{ 21 if(j < m && !(s1 & (1 << (k - 1)))) //可以横着铺 22 t += dp[i][j][s1 | (1 << k - 1) | (1 << k)][s2]; 23 t %= mod; 24 if(i < n && !(s2 & (1 << k))) //可以竖着铺 25 t += dp[i][j][s1 | (1 << k)][s2 | (1 << k)]; 26 t %= mod; 27 } 28 dp[i][j][s1][s2] += t % mod; 29 } 30 } 31 } 32 } 33 printf("%d ", dp[1][1][0][0]); 34 } 35 int main(){ 36 scanf("%d %d", &n, &m); 37 solve(); 38 }
题目:
#1048 : 状态压缩·二
描述
历经千辛万苦,小Hi和小Ho终于到达了举办美食节的城市!虽然人山人海,但小Hi和小Ho仍然抑制不住兴奋之情,他们放下行李便投入到了美食节的活动当中。美食节的各个摊位上各自有着非常多的有意思的小游戏,其中一个便是这样子的:
小Hi和小Ho领到了一个大小为N*M的长方形盘子,他们可以用这个盒子来装一些大小为2*1的蛋糕。但是根据要求,他们一定要将这个盘子装的满满的,一点缝隙也不能留下来,才能够将这些蛋糕带走。
这么简单的问题自然难不倒小Hi和小Ho,于是他们很快的就拿着蛋糕离开了~
但小Ho却不只满足于此,于是他提出了一个问题——他们有多少种方案来装满这个N*M的盘子呢?
值得注意的是,这个长方形盘子的上下左右是有区别的,如在N=4, M=3的时候,下面的两种方案被视为不同的两种方案哦!
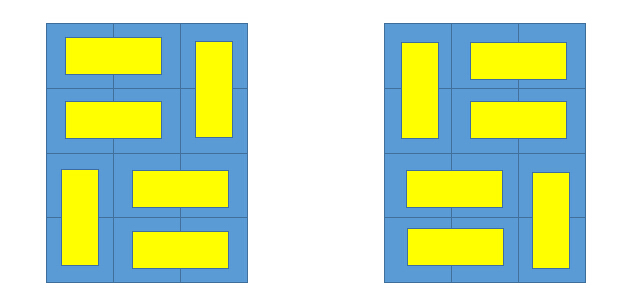
提示:我们来玩拼图吧!不过不同的枚举方式会导致不同的结果哦!
输入
每个测试点(输入文件)有且仅有一组测试数据。
每组测试数据的第一行为两个正整数N、M,表示小Hi和小Ho拿到的盘子的大小。
对于100%的数据,满足2<=N<=1000, 3<=m<=5。<>
输出
考虑到总的方案数可能非常大,只需要输出方案数除以1000000007的余数。
- 样例输入
-
2 4
- 样例输出
-
5