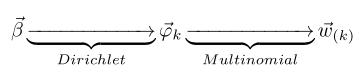LDA-math-LDA 文本建模

http://cos.name/2013/03/lda-math-lda-text-modeling/

5. LDA 文本建模

5.1 游戏规则

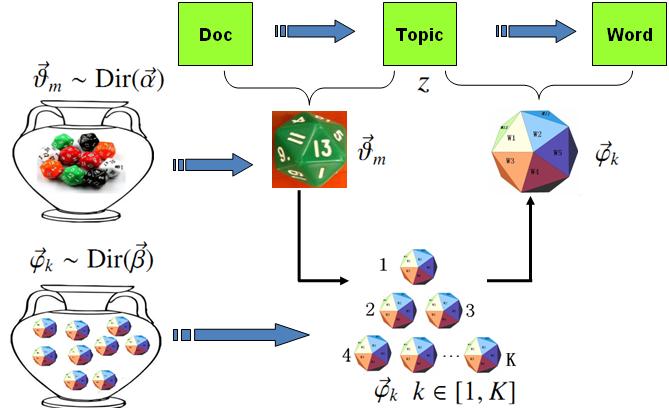
对于上述的 PLSA 模型，贝叶斯学派显然是有意见的，doc-topic 骰子θ→m和 topic-word 骰子φ→k都是模型中的参数，参数都是随机变量，怎么能没有先验分布呢？于是，类似于对 Unigram Model 的贝叶斯改造， 我们也可以如下在两个骰子参数前加上先验分布从而把 PLSA 对应的游戏过程改造为一个贝叶斯的游戏过程。由于 φ→k和θ→m都对应到多项分布，所以先验分布的一个好的选择就是Drichlet 分布，于是我们就得到了 LDA(Latent Dirichlet Allocation)模型。

LDA模型

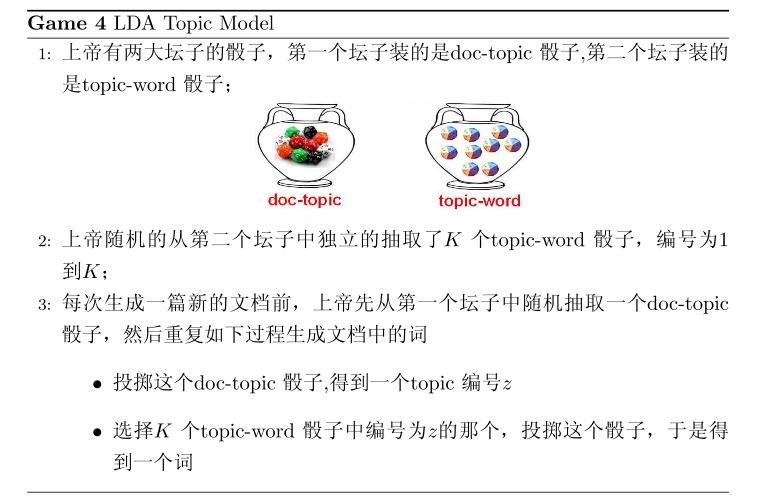
在 LDA 模型中, 上帝是按照如下的规则玩文档生成的游戏的

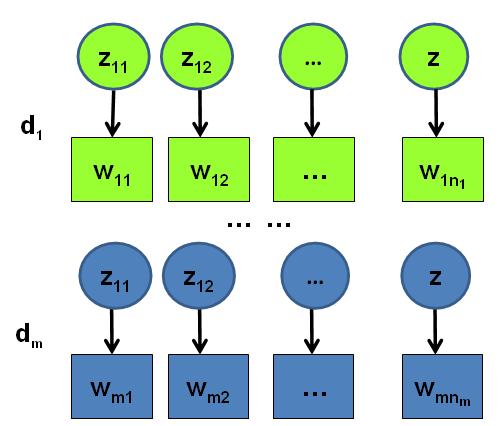
假设语料库中有 M 篇文档，所有的的word和对应的 topic 如下表示

w−→z→=(w→1,⋯,w→M)=(z→1,⋯,z→M)

其中， w→m 表示第m 篇文档中的词， z→m 表示这些词对应的 topic 编号。

语料生成过程中的 word 和 topic

5.2 物理过程分解

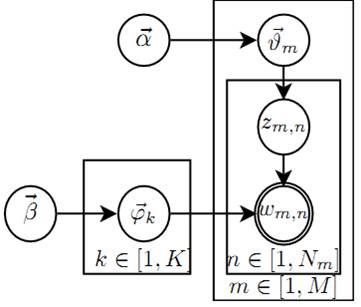
使用概率图模型表示， LDA 模型的游戏过程如图所示。

LDA概率图模型表示

这个概率图可以分解为两个主要的物理过程：

•  α→→θ→m→zm,n, 这个过程表示在生成第m 篇文档的时候，先从第一个坛子中抽了一个doc-topic 骰子 θ→m, 然后投掷这个骰子生成了文档中第 n 个词的topic编号zm,n；
•  β→→φ→k→wm,n|k=zm,n, 这个过程表示用如下动作生成语料中第m篇文档的第 n个词：在上帝手头的K 个topic-word 骰子 φ→k 中，挑选编号为 k=zm,n的那个骰子进行投掷，然后生成 word wm,n；

理解 LDA最重要的就是理解这两个物理过程。 LDA 模型在基于 K 个 topic 生成语料中的 M 篇文档的过程中， 由于是 bag-of-words 模型，有一些物理过程是相互独立可交换的。由此， LDA 生成模型中， M 篇文档会对应于 M 个独立的 Dirichlet-Multinomial 共轭结构； K 个 topic 会对应于 K 个独立的 Dirichlet-Multinomial 共轭结构。所以理解 LDA 所需要的所有数学就是理解 Dirichlet-Multiomail 共轭，其它都就是理解物理过程。现在我们进入细节， 来看看 LDA 模型是如何被分解为 M+K个Dirichlet-Multinomial 共轭结构的。

由第一个物理过程，我们知道 α→→θ→m→z→m 表示生成第 m 篇文档中的所有词对应的topics，显然 α→→θ→m 对应于 Dirichlet 分布， θ→m→z→m 对应于 Multinomial 分布， 所以整体是一个 Dirichlet-Multinomial 共轭结构；

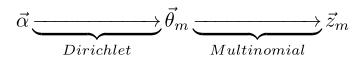
前文介绍 Bayesian Unigram Model 的小节中我们对 Dirichlet-Multinomial 共轭结构做了一些计算。借助于该小节中的结论，我们可以得到

p(z→m|α→)=Δ(n→m+α→)Δ(α→)

其中 n→m=(n(1)m,⋯,n(K)m)， n(k)m 表示第m篇文档中第k 个topic 产生的词的个数。进一步，利用 Dirichlet-Multiomial 共轭结构，我们得到参数 θ→m 的后验分布恰好是

Dir(θ→m|n→m+α→).

由于语料中 M篇文档的 topics 生成过程相互独立，所以我们得到 M 个相互独立的 Dirichlet-Multinomial 共轭结构，从而我们可以得到整个语料中 topics 生成概率

p(z→|α→)=∏m=1Mp(z→m|α→)=∏m=1MΔ(n→m+α→)Δ(α→)(∗)(1)

目前为止，我们由M篇文档得到了 M 个 Dirichlet-Multinomial 共轭结构，还有额外K 个 Dirichlet-Multinomial 共轭结构在哪儿呢？在上帝按照之前的规则玩 LDA 游戏的时候，上帝是先完全处理完成一篇文档，再处理下一篇文档。文档中每个词的生成都要抛两次骰子，第一次抛一个doc-topic骰子得到 topic, 第二次抛一个topic-word骰子得到 word，每次生成每篇文档中的一个词的时候这两次抛骰子的动作是紧邻轮换进行的。如果语料中一共有 N 个词，则上帝一共要抛 2N次骰子，轮换的抛doc-topic骰子和 topic-word骰子。但实际上有一些抛骰子的顺序是可以交换的，我们可以等价的调整2N次抛骰子的次序：前N次只抛doc-topic骰子得到语料中所有词的 topics,然后基于得到的每个词的 topic 编号，后N次只抛topic-word骰子生成 N 个word。于是上帝在玩 LDA 游戏的时候，可以等价的按照如下过程进行：

以上游戏是先生成了语料中所有词的 topic, 然后对每个词在给定 topic 的条件下生成 word。在语料中所有词的 topic 已经生成的条件下，任何两个 word 的生成动作都是可交换的。于是我们把语料中的词进行交换，把具有相同 topic 的词放在一起

w−→′z→′=(w→(1),⋯,w→(K))=(z→(1),⋯,z→(K))

其中，w→(k) 表示这些词都是由第 k 个 topic 生成的， z→(k) 对应于这些词的 topic 编号，所以z→(k)中的分量都是k。

对应于概率图中的第二个物理过程 β→→φ→k→wm,n|k=zm,n，在 k=zm,n的限制下，语料中任何两个由 topic k 生成的词都是可交换的，即便他们不再同一个文档中，所以我们此处不再考虑文档的概念，转而考虑由同一个 topic 生成的词。考虑如下过程 β→→φ→k→w→(k) ，容易看出， 此时 β→→φ→k 对应于 Dirichlet 分布， φ→k→w→(k) 对应于 Multinomial 分布， 所以整体也还是一个 Dirichlet-Multinomial 共轭结构；

同样的，我们可以得到

p(w→(k)|β→)=Δ(n→k+β→)Δ(β→)

其中 n→k=(n(1)k,⋯,n(V)k)， n(t)k 表示第k 个topic 产生的词中 word t的个数。进一步，利用 Dirichlet-Multiomial 共轭结构，我们得到参数 φ→k 的后验分布恰好是

Dir(φ→k|n→k+β→).

而语料中 K个 topics 生成words 的过程相互独立，所以我们得到 K 个相互独立的 Dirichlet-Multinomial 共轭结构，从而我们可以得到整个语料中词生成概率

p(w−→|z→,β→)=p(w−→′|z→′,β→)=∏k=1Kp(w→(k)|z→(k),β→)=∏k=1KΔ(n→k+β→)Δ(β→)(∗∗)(2)

结合 (*)  和 (**) 于是我们得到

p(w−→,z→|α→,β→)=p(w−→|z→,β→)p(z→|α→)=∏k=1KΔ(n→k+β→)Δ(β→)∏m=1MΔ(n→m+α→)Δ(α→)(∗∗∗)(3)

此处的符号表示稍微不够严谨, 向量 n→k, n→m 都用 n 表示， 主要通过下标进行区分，k 下标为 topic 编号, m 下标为文档编号。

5.3 Gibbs Sampling

有了联合分布 p(w−→,z→), 万能的 MCMC 算法就可以发挥作用了！于是我们可以考虑使用 Gibbs Sampling 算法对这个分布进行采样。当然由于 w−→ 是观测到的已知数据，只有 z→是隐含的变量，所以我们真正需要采样的是分布 p(z→|w−→)。在 Gregor Heinrich 那篇很有名的LDA 模型科普文章 Parameter estimation for text analysis 中，是基于 (***) 式推导 Gibbs Sampling 公式的。此小节中我们使用不同的方式，主要是基于 Dirichlet-Multinomial 共轭来推导 Gibbs Sampling 公式，这样对于理解采样中的概率物理过程有帮助。

语料库z→ 中的第i个词我们记为zi, 其中i=(m,n)是一个二维下标，对应于第m篇文档的第 n个词，我们用 ¬i 表示去除下标为i的词。那么按照 Gibbs Sampling 算法的要求，我们要求得任一个坐标轴 i 对应的条件分布 p(zi=k|z→¬i,w−→) 。假设已经观测到的词 wi=t, 则由贝叶斯法则，我们容易得到

p(zi=k|z→¬i,w−→)∝p(zi=k,wi=t|z→¬i,w−→¬i)

由于zi=k,wi=t 只涉及到第 m 篇文档和第k个 topic，所以上式的条件概率计算中, 实际上也只会涉及到如下两个Dirichlet-Multinomial 共轭结构

1.  α→→θ→m→z→m
2. β→→φ→k→w→(k)

其它的 M+K−2 个 Dirichlet-Multinomial 共轭结构和zi=k,wi=t是独立的。

由于在语料去掉第i 个词对应的 (zi,wi)，并不改变我们之前讨论的 M+K 个 Dirichlet-Multinomial 共轭结构，只是某些地方的计数会减少。所以θ→m,φ→k 的后验分布都是 Dirichlet:

p(θ→m|z→¬i,w−→¬i)p(φ→k|z→¬i,w−→¬i)=Dir(θ→m|n→m,¬i+α→)=Dir(φ→k|n→k，¬i+β→)

使用上面两个式子，把以上想法综合一下，我们就得到了如下的 Gibbs Sampling 公式的推导

=
=
=
=
=
=
=

p(zi=k|z→¬i,w−→)∝p(zi=k,wi=t|z→¬i,w−→¬i)=∫p(zi=k,wi=t,θ→m,φ→k|z→¬i,w−→¬i)dθ→mdφ→k=∫p(zi=k,θ→m|z→¬i,w−→¬i)⋅p(wi=t,φ→k|z→¬i,w−→¬i)dθ→mdφ→k=∫p(zi=k|θ→m)p(θ→m|z→¬i,w−→¬i)⋅p(wi=t|φ→k)p(φ→k|z→¬i,w−→¬i)dθ→mdφ→k=∫p(zi=k|θ→m)Dir(θ→m|n→m,¬i+α→)dθ→m⋅∫p(wi=t|φ→k)Dir(φ→k|n→k,¬i+β→)dφ→k=∫θmkDir(θ→m|n→m,¬i+α→)dθ→m⋅∫φktDir(φ→k|n→k,¬i+β→)dφ→k=E(θmk)⋅E(φkt)=θ^mk⋅φ^kt

以上推导估计是整篇文章中最复杂的数学了，表面上看上去复杂，但是推导过程中的概率物理意义是简单明了的：zi=k,wi=t的概率只和两个 Dirichlet-Multinomial 共轭结构关联。而最终得到的 θ^mk,φ^kt 就是对应的两个 Dirichlet 后验分布在贝叶斯框架下的参数估计。借助于前面介绍的Dirichlet 参数估计的公式 ，我们有

θ^mkφ^kt=n(k)m,¬i+αk∑Kk=1(n(k)m,¬i+αk)=n(t)k,¬i+βt∑Vt=1(n(t)k,¬i+βt)

于是，我们最终得到了 LDA 模型的 Gibbs Sampling 公式

p(zi=k|z→¬i,w−→)∝n(k)m,¬i+αk∑Kk=1(n(k)m,¬i+αk)⋅n(t)k,¬i+βt∑Vt=1(n(t)k,¬i+βt)(4)

这个公式是很漂亮的， 右边其实就是 p(topic|doc)⋅p(word|topic)，这个概率其实是 doc→topic→word 的路径概率，由于topic 有K 个，所以 Gibbs Sampling 公式的物理意义其实就是在这K 条路径中进行采样。

doc-topic-word 路径概率

5.4 Training and Inference

有了 LDA 模型，当然我们的目标有两个

• 估计模型中的参数 φ→1,⋯,φ→K 和 θ→1,⋯,θ→M；
• 对于新来的一篇文档docnew，我们能够计算这篇文档的 topic 分布θ→new。

有了 Gibbs Sampling 公式， 我们就可以基于语料训练 LDA 模型，并应用训练得到的模型对新的文档进行 topic 语义分析。训练的过程就是获取语料中的 (z,w) 的样本，而模型中的所有的参数都可以基于最终采样得到的样本进行估计。训练的流程很简单:

对于 Gibbs Sampling 算法实现的细节，请参考 Gregor Heinrich 的 Parameter estimation for text analysis 中对算法的描述，以及 PLDA(http://code.google.com/p/plda) 的代码实现，此处不再赘述。

由这个topic-word 频率矩阵我们可以计算每一个p(word|topic)概率，从而算出模型参数φ→1,⋯,φ→K, 这就是上帝用的 K 个 topic-word 骰子。当然，语料中的文档对应的骰子参数 θ→1,⋯,θ→M 在以上训练过程中也是可以计算出来的，只要在 Gibbs Sampling 收敛之后，统计每篇文档中的 topic 的频率分布，我们就可以计算每一个 p(topic|doc) 概率，于是就可以计算出每一个θ→m。由于参数θ→m 是和训练语料中的每篇文档相关的，对于我们理解新的文档并无用处，所以工程上最终存储 LDA 模型时候一般没有必要保留。通常，在 LDA 模型训练的过程中，我们是取 Gibbs Sampling 收敛之后的 n 个迭代的结果进行平均来做参数估计，这样模型质量更高。

有了 LDA 的模型，对于新来的文档 docnew, 我们如何做该文档的 topic 语义分布的计算呢？基本上 inference 的过程和 training 的过程完全类似。对于新的文档， 我们只要认为 Gibbs Sampling 公式中的 φ^kt 部分是稳定不变的，是由训练语料得到的模型提供的，所以采样过程中我们只要估计该文档的 topic 分布θ→new就好了。

6. 后记

LDA 对于专业做机器学习的兄弟而言，只能算是一个简单的Topic Model。但是对于互联网中做数据挖掘、语义分析的工程师，LDA 的门槛并不低。 LDA 典型的属于这样一种机器学习模型：要想理解它，需要比较多的数学背景，要在工程上进行实现，却相对简单。 Gregor Heinrich 的LDA 模型科普文章 Parameter estimation for text analysis 写得非常的出色，这是学习 LDA 的必看文章。不过即便是这篇文章，对于工程师也是有门槛的。我写的这个科普最好对照 Gregor Heinrich 的这篇文章来看， 我用的数学符号也是尽可能和这篇文章保持一致。

这份LDA 科普是基于给组内兄弟做报告的 ppt 整理而成的，说是科普其实也不简单，涉及到的数学还是太多。在工业界也混了几年，经常感觉到工程师对于学术界的玩的模型有很强的学习和尝试的欲望，只是学习成本往往太高。所以我写 LDA 的初衷就是写给工业界的工程师们看的，希望把学术界玩的一些模型用相对通俗的方式介绍给工程师；如果这个科普对于读研究生的一些兄弟姐妹也有所启发，只能说那是一个 side effect :-)。

我个人很喜欢LDA ，它是在文本建模中一个非常优雅的模型，相比于很多其它的贝叶斯模型， LDA 在数学推导上简洁优美。学术界自 2003 年以来也输出了很多基于LDA 的 Topic Model 的变体，要想理解这些更加高级的 Topic Model, 首先需要很好的理解标准的 LDA 模型。在工业界， Topic Model 在 Google、Baidu 等大公司的产品的语义分析中都有着重要的应用；所以Topic Model 对于工程师而言，这是一个很有应用价值、值得学习的模型。我接触 Topic Model 的时间不长，主要是由于2年前和 PLDA 的作者 Wangyi 一起合作的过程中，从他身上学到了很多 Topic Model 方面的知识。关于 LDA 的相关知识，其实可以写的还有很多：如何提高 LDA Gibbs Sampling 的速度、如何优化超参数、如何做大规模并行化、LDA 的应用、LDA 的各种变体…… 不过我的主要目标还是科普如何理解标准的LDA 模型。

学习一个模型的时候我喜欢追根溯源，常常希望把模型中的每一个数学推导的细节搞明白，把公式的物理意义想清楚，不过数学推导本身并不是我想要的，把数学推导还原为物理过程才是我乐意做的事。最后引用一下物理学家费曼的名言结束 LDA 的数学科普：

What I cannot create, I do not understand. 
— Richard Feynman

LDA数学八卦

LDA-math 的汇总， “LDA数学八卦.pdf” 我整理贴出来了， 希望对大家理解 LDA 有帮助。 文章标题挂上“八卦”两字， 因为八卦意味着形式自由、不拘束、可以天马行空，细节处理上也难免有不严谨的地方；当然我也希望八卦是相对容易理解的。

前排留名。等了好久终于等到了LDA。
为同学们节约搜索时间，plsa的连接如下
http://cs.brown.edu/~th/papers/Hofmann-UAI99.pdf
Blei的LDA也有简单的review PLSA，unigram model
http://www.cs.princeton.edu/~blei/papers/BleiNgJordan2003.pdf
08年Blei同学来了次回锅肉，把lda改进改进。在LDA里，topic之间是独立的，但是有时候应该是有影响的；所以，换另一个先验分布
http://www.cs.cmu.edu/~lafferty/pub/ctm.pdf