这题把我写吐了。。。代码水平还是太弱鸡了啊。。。
这题就是先给你一些点,以及点权。然后给你一些向边构成一颗树,树的根节点是1。
然后给定三个操作
第一个是把指定节点的权值+W
第二个是把指定节点X为根(包括自己)的所有点权+W
第三个是求出指定节点到根节点的点权之和
嗯没错,听了大佬讲,肯定跑不了是DFS序,那么是用哪种呢???是N的还是2N的??
我们思考一个问题,如果是N的,能表示什么遍历完成儿子节点的时间吗???显然不能
但是。。。2n的是可以的,因为节点DFS出现两次中间的节点都是他的儿子。
如果知道DFS序列,上面1.2操作显然是不足为虑的。。。但是3操作呢???我们如果单纯求和,那么有些没有走过的点会计算两次,
不妨这样考虑:我们写出DFS序
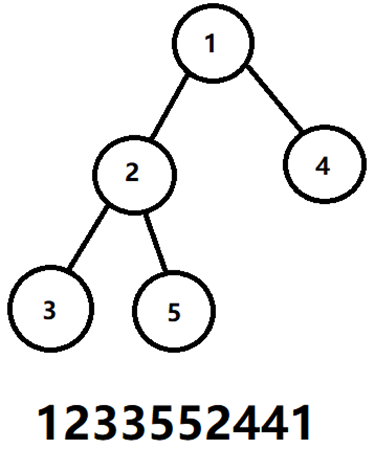
如果求5到根节点,我们会求出12(33)5,每个数前后的位置,我们可以用一个数组存储(这非常简单),我们能不能想办法消去这个影响呢???
这是没问题的,我来思考一下,如果我依照某个DFS序,到底起点,那么DFS序中出现两次的一定是没用的,我们统计内部内部只出现一次数的个数,这个些个数就是操作3在这个区间的效果。
但是还有一个问题,我们如果抵消了,那么是不是GG了?我以后访问这个数岂不是也完蛋了?但题目要求跟新的整个子树,我如果这样抵消。。。会对以后造成影响吗??
其实是不会的,因为我们是把加的值放在了这个数第一次出现的地方,把减的值放在了第二次出现的地方。我们实际上对后面不会有影响,如果要访问节点x以及其子树,一定不会访问到第二个节点x出现的位置。
#include<iostream> #include<stdio.h> #include<string.h> #include<algorithm> #include<vector> #define LL long long using namespace std; const int maxx = 1e6+5; struct node{ int l,r; LL sum,laze; }tree[maxx<<2]; struct snode{ int pre,bac; }id[maxx]; vector<int>G[maxx]; int vis[maxx]; int st[maxx]; int num[maxx],a[maxx],b[maxx],c[maxx]; int n,m; int cnt; int num_s; inline int L(int x){return x<<1;}; inline int R(int x){return x<<1|1;}; inline int MID(int l,int r){return (l+r)>>1;}; void push_down(int root){ if (tree[root].laze){ tree[L(root)].laze+=tree[root].laze; tree[R(root)].laze+=tree[root].laze; tree[L(root)].sum+=(LL)(num[tree[L(root)].r]-num[tree[L(root)].l-1])*tree[root].laze; tree[R(root)].sum+=(LL)(num[tree[R(root)].r]-num[tree[R(root)].l-1])*tree[root].laze; tree[root].laze=0; } } void buildtree(int root,int l,int r){ tree[root].l=l; tree[root].r=r; tree[root].laze=0; tree[root].sum=0; if (l==r){ tree[root].sum=(LL)(num[l]-num[l-1])*a[st[l]]; return; } int mid=MID(l,r); buildtree(L(root),l,mid); buildtree(R(root),mid+1,r); tree[root].sum=tree[L(root)].sum+tree[R(root)].sum; } void update(int root,int ul,int ur,int w){ int l=tree[root].l; int r=tree[root].r; if (ul<=l && r<=ur){ tree[root].sum+=(LL)(num[r]-num[l-1])*w; tree[root].laze+=w; return; } push_down(root); int mid=MID(l,r); if (ur<=mid){ update(L(root),ul,ur,w); }else if(ul>mid){ update(R(root),ul,ur,w); }else{ update(L(root),ul,mid,w); update(R(root),mid+1,ur,w); } tree[root].sum=tree[L(root)].sum+tree[R(root)].sum; } LL query(int root,int ql,int qr){ int l=tree[root].l; int r=tree[root].r; int mid; LL sum=0; if (ql<=l && r<=qr){ return tree[root].sum; } mid=MID(l,r); push_down(root); if (qr<=mid){ sum+=query(L(root),ql,qr); }else if (ql>mid){ sum+=query(R(root),ql,qr); }else { sum+=query(L(root),ql,mid); sum+=query(R(root),mid+1,qr); } return sum; } void dfs(int x) { vis[x]=1; cnt++; num[cnt]=1; st[cnt]=x; c[x]=cnt; id[x].pre=cnt; for (int i=0;i<G[x].size();i++) { if(!vis[G[x][i]]){ dfs(G[x][i]); } } cnt++; id[x].bac=cnt; st[cnt]=x; num[cnt]=-1; } int main() { int u,v,op,tmp1,tmp2; while(~scanf("%d%d",&n,&m)) { for (int i=1;i<=n;i++){ G[i].clear(); } cnt=0; num_s=0; memset(vis,0,sizeof(vis)); memset(tree,0,sizeof(tree)); for (int i=1;i<=n;i++){ scanf("%d",&a[i]); } for (int i=1; i<n; i++) { scanf("%d%d",&u,&v); G[u].push_back(v); G[v].push_back(u); } dfs(1); num[0]=0; for (int i=1;i<=2*n;i++){ num[i]=num[i-1]+num[i]; } buildtree(1,1,2*n); while(m--){ scanf("%d",&op); if (op==1){ scanf("%d%d",&tmp1,&tmp2); update(1,id[tmp1].pre,id[tmp1].pre,tmp2); update(1,id[tmp1].bac,id[tmp1].bac,tmp2); }else if (op==2){ scanf("%d%d",&tmp1,&tmp2); update(1,id[tmp1].pre,id[tmp1].bac,tmp2); }else { scanf("%d",&tmp1); printf("%lld ",query(1,1,id[tmp1].pre));; } } } return 0; } /* */