二进制(binary)在数学和数字电路中指以2为基数的记数系统,以2为基数代表系统是二进位制的。这一系统中,通常用两个不同的符号0(代表零)和1(代表一)来表示。数字电子电路中,逻辑门的实现直接应用了二进制,因此现代的计算机和依赖计算机的设备里都用到二进制。每个数字称为一个比特(Bit,Binary digit的缩写)
-
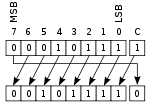
数的二进制表示及按位操作
二进制数值表示,举例:
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
右开始基于"0"索引号 |
|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
位权值 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
二进制数,N = 00100010 |
|
H |
G |
F |
E |
D |
C |
B |
A |
字母标签索引 |
在此例中,整数N = 34(DEC)=100010(BIN),还可以用集合方式表示:{1,5}、{B,F},因为整数N的1、5号位为1(从右边往左边开始计数),字母标签索引同理。
-
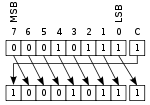
按位非操作(NOT)
按位非(NOT)或求补(complement)操作,是一元运算里执行逻辑否定每一位,在给定的二进制值产生它的反码值(one's complement)。位值是0变为1,位值是1变为0。例如:
A = 10101011
NOT A = 01010100
许多程序设计语言(包括C程序设计语言family),取反操作符用波浪线"~"表示。值得注意的是此操作符与"逻辑非(!)"操作符不同。在C++中,逻辑非将数字整体看做一个布尔类型--将真值转化为假,将假值转化为真;而C语言将0转化为1,将非零值转化为0。"逻辑非"并不是一个位操作。
对于无符号整数,一个数的按位补码是该数在无符号整数范围的中点上的"镜像反射",举例在二进制8位的无符号整数,NOT X = 255 - X(1111 1111dec = 255bin)。可以在图形上显示为向下的一条线,有效地"翻转"从0到255的递增范围,从255到0的递减范围。一个简单但说明性的示例用法是反转灰度图像,其中每个像素都存储为无符号整数。
举例四位的二进数无符号数,其值是0000~1111,十进制表示范围:0~15;十六进制表示范围:0~F。同理扩展到8位、16位、32位无符号整数。
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
F |
E |
D |
C |
B |
A |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
NOT 0010 = 1101, 即1111 - 0010 = 1101, 0010(bin) = 2(oct),1102(bin)=D(oct)。以1为起步索引号,索引"3"对应"14",值"2"对应值"D",都是基于值"7"与"8"中间为分隔的对称。
灰度反转(值:0~255):
|
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
-
按位与操作 (AND)
按位与(AND)是一种二进制运算,它采用两个等长的二进制表示形式,并对每对对应的位执行逻辑与运算,等效于将它们相乘。因此,如果比较位置的两个位均为1,则结果二进制表示中的位为1(1×1 = 1);否则结果为0(1×0 = 0和0×0 = 0)。
0101 (decimal 5)
AND 0011 (decimal 3)
= 0001 (decimal 1)
该操作可用于确定是将特定位设置为(1)还是将其清除(0)。例如,给定一个位模式0011(十进制3),要确定是否设置了第二位,我们使用按位与,并且在第二位中仅包含1的位模式:
0011 (decimal 3)
AND 0010 (decimal 2)
= 0010 (decimal 2)
因为结果0010不为零,所以我们知道原始模式中的第二个位已设置。这通常称为位屏蔽。 (类比地,使用遮盖胶带遮盖或遮盖不应更改的部分或不感兴趣的部分。在这种情况下,0值将遮盖不感兴趣的位。)
按位与可用于清除寄存器的选定位(或标志),其中每个位代表一个单独的布尔状态。此技术是使用尽可能少的内存来存储许多布尔值的有效方法。
例如,可以将0110(十进制6)视为四个标志的集合,其中第一个和第四个标志被清除(0),第二和第三个标志被设置为(1)。通过使用按位与,仅在第三位具有零的模式,可以清除第三标志:
0110 (decimal 6)
AND 1011 (decimal 11)
= 0010 (decimal 2)
由于此属性,通过检查最低位的值来检查二进制数的奇偶校验变得容易。使用上面的示例:
0110 (decimal 6)
AND 0001 (decimal 1)
= 0000 (decimal 0)
由于6 AND 1为零,因此6可被二整除,因此是偶数。
总结:
x AND 1 = x get
x AND 0 = 0 clear(reset)
-
按位或操作 (OR)
x OR 1 = 1 set
x OR 0 = X get
按位或运算是一种二进制运算,采用相等长度的两个位模式,并在每对对应位上执行逻辑"或"运算。如果两个位均为0,则每个位置的结果为0,否则,结果为1。例如:
0101 (decimal 5)
OR 0011 (decimal 3)
= 0111 (decimal 7)
按位或可用于将寄存器的选定位设置为1。例如,可以通过对仅设置了第四位的模式执行按位"或"来设置0010的第四位(十进制2):
0010 (decimal 2)
OR 1000 (decimal 8)
= 1010 (decimal 10)
总结:
x OR 1 = 1 set
x OR 0 = X get
-
按位异或操作 (XOR)
按位XOR是一种二进制操作,它采用两个长度相等的位模式,并对每对对应位执行逻辑异或运算。如果仅第一个位为1或仅第二个位为1,则每个位置的结果为1;但是如果两个都为0或都为1,则结果为0。在此,我们对两个位进行比较,如果两个位为1位不同,如果相同,则返回0。例如:
0101 (decimal 5)
XOR 0011 (decimal 3)
= 0110 (decimal 6)
按位XOR可用于反转寄存器中的选定位(也称为切换或翻转)。可以通过与1进行异或来切换任何位。例如,给定位模式0010(十进制2),第二和第四位可以通过按位异或在第二和第四位置中包含1的位模式来切换:
0010 (decimal 2)
XOR 1010 (decimal 10)
= 1000 (decimal 8)
汇编语言程序员和优化编译器有时将XOR用作将寄存器的值设置为零的捷径。对自己的值执行XOR运算始终会产生零,并且在许多体系结构上,此操作所需的时钟周期和内存比加载零值并将其保存到寄存器要少。
总结:
x XOR 1 = NOT x invert
x XOR 0 = x get
应用一,所有复位:
0110
XOR 0110
= 0000
应用二, 交换两个数:
x ^= y;
y ^= x;
x ^= y;
或
new_y = y ^ (x ^ y) = x;
new_x = x ^ (x ^ y) = y;
-
NAND与非操作
-
NOR 或非操作
-
XNOR 异或非操作
-
所有二进制逻辑运算符的真值表
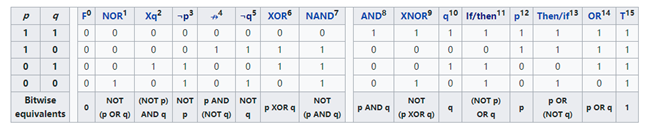
两个二进制变量有16个可能的真值函数,它定义了一个真值表。
这是两个位P和Q的按位等效运算:
|
运算 |
说明 |
|
AND |
如果所有输入均为 TRUE,则为 TRUE |
|
OR |
如果至少有一个输入为 TRUE,则为 TRUE |
|
NAND |
如果至少有一个输入为 FALSE,则为 TRUE |
|
NOR |
如果所有输入均不为 TRUE,则为 TRUE |
|
XOR |
如果有奇数个输入为 TRUE,则为 TRUE |
|
NXOR |
如果有偶数个输入为 TRUE,则为 TRUE |
|
NOT |
如果输入为 FALSE,则为 TRUE |
-
移位(bit shifts)
位移有时被认为是按位运算,因为它们将值视为一系列位而不是数值。在这些操作中,数字将向左或向右移动或移位。计算机处理器中的寄存器具有固定的宽度,因此某些位将在一端从寄存器中"移出",而相同数量的位从另一端"移入"。移位运算符之间的差异在于它们如何确定移入位的值。
-
位寻址
如果寄存器的宽度(通常为32或什至64)大于最小可寻址单元(原子元素)的位数(通常为8),通常称为字节,则移位操作会在这些位上引入寻址方案。忽略寄存器两端的边界效应,算术和逻辑移位操作的行为相同,移位8位位置可以按以下方式将位模式传输1个字节位置:
小端顺序:左移8位将字节地址增加1
小端顺序:向右移8位将字节地址减少1
大端顺序:左移8位将字节地址减1
大端顺序:向右移8位将字节地址增加1
-
算术移位
在算术移位中,从任一端移出的位都将被丢弃。在左算术移位中,零右移入最右位。向右算术移位时,符号位(二进制补码的MSB)向左移,从而保留了操作数的符号。
示例使用一个8位寄存器:
00010111 (decimal +23) LEFT-SHIFT
= 00101110 (decimal +46)
10010111 (decimal −105) RIGHT-SHIFT
= 11001011 (decimal −53)
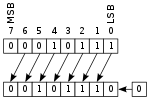
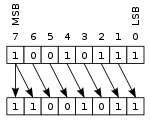
在第一种情况下,最左边的数字移到寄存器的末尾,新的0移到最右边的位置。在第二种情况下,最右边的1移出(可能移入进位标志),新的1复制到最左边的位置,并保留数字的符号。有时将多个班次缩短为单个班次数位。
00010111 (decimal +23) LEFT-SHIFT-BY-TWO
= 01011100 (decimal +92)
左算术移位等于n乘以2n(前提是该值不会溢出),而右算术移位等于2的补码值的n等于除以2n并向负无穷大舍入。如果将二进制数视为补码,则相同的右移运算将导致被2n除并向零舍入。
-
逻辑移位
在逻辑移位中,将零移入以替换丢弃的位。因此,逻辑和算术左移是完全相同的。但是,由于逻辑右移将值0位插入最高有效位,而不是复制符号位,因此对于无符号二进制数是理想的,而算术右移对于有符号二进制补码二进制数是理想的。
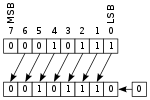

-
循环移位
移位的另一种形式是循环移位,按位旋转或位旋转。
-
环绕/旋转
在此操作中,有时称为"旋转不进位",位被"旋转",就好像寄存器的左右两端相连。在左移期间向右移的值是向左移出的值,对于右移操作反之亦然。如果有必要保留所有现有位,这很有用,并且在数字加密中经常使用。
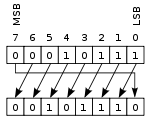

-
旋转进位
进位进位是循环操作的一种变体,其中(任一端)移入的位是进位标志的旧值,而(另一端)移出的位变为的新值。进位标志。
一次循环进位可以通过预先设置进位标志来模拟一个位置的逻辑或算术移位。例如,如果进位标志包含0,则x RIGHT-ROTATE-THROUGH-CARRY-BY-BY是逻辑右移,如果进位标志包含符号位的副本,则x RIGHT-ROTATE-THROUGH -CARRY-BY-ONE是一种算术右移。因此,某些微控制器(例如低端PIC)只是旋转并通过进位旋转,而不会为算术或逻辑移位指令所困扰。
当对大于处理器本机字大小的数字进行移位时,循环进位转换特别有用,因为如果将大量存储在两个寄存器中,则从第一个寄存器的一端移出的位必须位于寄存器的另一端。第二。使用直进式进位时,该位在第一次移位期间被"保存"在进位标志中,准备在第二次移位期间进行移位而无需任何额外的准备。