Codeforces Round #645 (Div. 2) (A)

A Park Lighting

题意：这一题的题意可以简单理解成，给你一个n*m的矩阵，要你用1*2的矩阵去填充（可以缩小为1*1的矩阵），问要将原矩阵填满，最少需要多少个小的矩阵。

如下图所示：

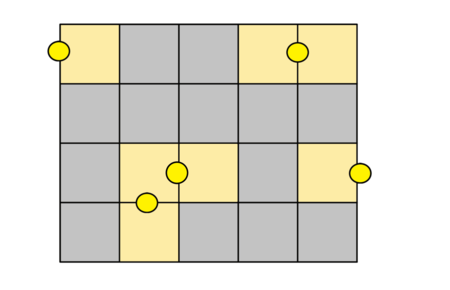
题解：这一比较简单，同时也可以用很多的写法来写，直接法or规律法。这里主要介绍一下规律法：

　　当n与m其中有一个数字为偶数的时候，我们可以让边长为2的顺着那个偶数的方向摆放，最后得到的数量一定是最少的。

　　sum=n*m/2

　　当两个数都为奇数的时候，我们可以将其进行转换为上一种情况来计算：取一列出来单独计算，剩下的为n*（m-1）这种符合上一种情况:sum=n*(m-1)/2;而单独拿出来的那一列为：sum=（n-1)/2 + 1;

代码：

法一：

#include<iostream>
#include<cstring>
#include<queue>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
priority_queue <ll,vector<ll>,greater<ll> > q;
int main() {
    ll t;
    ll n,m;/*n 行 m 列*/
    cin>>t;
    while(t--){
        cin>>n>>m;/*n 行 m 列*/
        ll ans=0;
        if(n%2==0){//偶数 行 
            if(m%2==0){/*偶数列*/
                int t1=n/2,t2=m/2;
                ans=t1*t2*2;
            }else{/*奇数列*/
                int t1=n/2;
                if(m==1){/*只有 一列*/
                    ans=t1;
                }else{// 3 5 7 9 之类 
                    int t2=m/2;
                    ans=t1*t2*2+t1;
                }
            } 
        }else{/*奇数行*/
            if(n==1){//只有 一 行 
                if(m%2==0){
                    ans=m/2;
                }else{/*奇数列*/
                    ans=m/2+1;
                }
            } else{//有多行 
                int t1=n/2;
                if(m%2==0){//偶数列 
                    int t2=m/2;
                    ans=t1*t2*2+t2;
                }else{//奇数列 
                    if(m==1){//只有一列 
                        ans=t1+1;
                    }else{//有 多列  3 5 7 9之类 
                        int t2=m/2;
                        ans=t1*t2*2+t2+t1+1;
                    }
                }
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

法二：

#include<iostream>
using namespace std;
int main(){
    int t,n,m;
    cin>>t;
    while(t--){
        cin>>n>>m;
        int sum=0;
        if(n%2==0||m%2==0){
            sum=n*m / 2;
        }else{
            sum=(n*(m-1))/2 + (n-1)/2 +1;
        }
        
        cout<<sum<<endl;
    }
    return 0;
}