Tarjan学习笔记

引言

在有向图$G$中，如果两个节点能够相互到达，那么这就是一个连通分量，如果每两个节点都连通，那么这就是一个强联通图。

有向图的极大强连通子图成为一个强连通分量，而$Tarjan$算法便是用来求强连通分量的算法。

算法介绍

$Tarjan$算法是由$Robert Tarjan$提出的，该算法时间复杂度为$O(N+M)$，属于线性复杂度。

再此膜拜神仙   $\%\%\% STO Tarjan ORZ \%\%\%$

$Tarjan$算法是用$DFS$实现的算法，在一棵搜索树当中，每一个强连通分量都是一个子树

定义$DFN(U)$表示节点$U$被访问到的次序编号，$LOW(U)$表示节点$U$或者$U$的子树在退栈时所能遍历到的最小的次序编号

显而易见，当$DFN(U) == LOW(U)$时，以$U$节点为$root$的子树就是一个强联通分量。

我们在遍历的时候，如果先将当前的节点压入栈中，由$vis$数组对其进行标记，表示已经入过栈然后遍历这个节点的所有边

如果边的终点的$DFN$已经有值了，就代表$DFN$已经访问过了，那么就不需要对其进行遍历，只需要确定它与当前节点的关系

否则就对其进行遍历，在回溯的时候将其$LOW$值与经过的点进行比较取最小值

下面是$Tarjan$算法的伪代码，来自BYvoid大神的blog，如果你想进去，请先挂上梯子

tarjan(u)
{
    DFN[u]=Low[u]=++Index                      // 为节点u设定次序编号和Low初值
    Stack.push(u)                              // 将节点u压入栈中
    for each (u, v) in E                       // 枚举每一条边
        if (v is not visted)               // 如果节点v未被访问过
            tarjan(v)                  // 继续向下找
            Low[u] = min(Low[u], Low[v])
        else if (v in S)                   // 如果节点v还在栈内
            Low[u] = min(Low[u], DFN[v])
    if (DFN[u] == Low[u])                      // 如果节点u是强连通分量的根
        repeat
            v = S.pop                  // 将v退栈，为该强连通分量中一个顶点
            print v
        until (u== v)
}

流程演示

接下来的图片也是来自BYvoid的blog，

注：左边的绿色的框框代表堆栈，最底下是栈顶哦^(*￣(oo)￣)^

step1

先从节点$1$开始遍历，一直遍历到节点$6$，$LOW(6) == DFN(6)$，说明节点$6$就是一个强连通分量

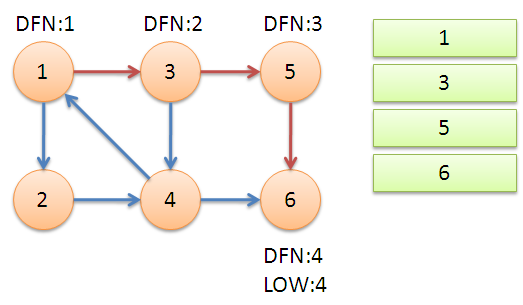
step2

回溯到节点$5$之后，发现$LOW(5) == DFN(5)$，同理，节点$5$也是一个强连通分量

step3

继续回溯到节点$3$，发现节点$3$还有边可以走，遍历到节点$4$，用从节点$4$遍历到$1$，这时发现$1$已经在栈里了。节点$4$的$LOW$值就变成了$1$

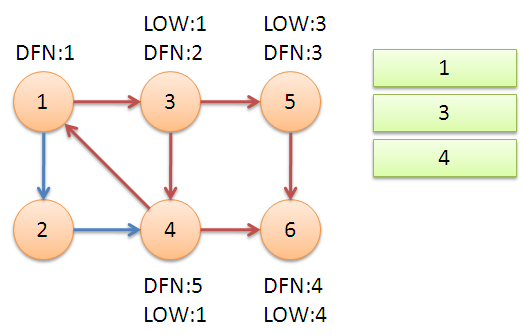
step4

继续回溯，回溯到节点$1$之后，又遍历到节点$2$，又从节点$2$遍历到节点$4$，这时发现$4$已经在栈里了，同理，节点$2$的$LOW$值将变成$5$，因为是将节点$4$的$DFN$值和节点$2$的$LOW$值取最小值

然后回溯到节点$1$，发现节点$1$的$LOW$值和$DFN$值相等，就开始退栈，一直到栈顶元素不等于$1$

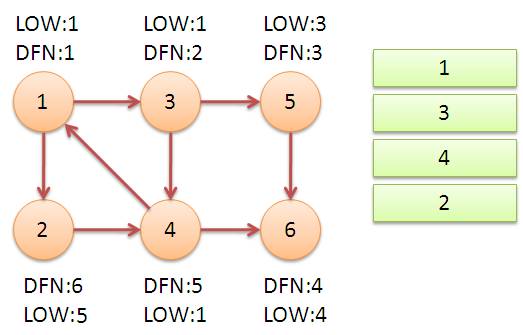
至此，该算法完成，这张图一共有三个强连通分量，分别是

1 2 3 4
5
6

　 

复杂度分析

至于$Tarjan$算法的复杂度，因为每个节点只入过一次栈，并且每条边只访问过一次，所以它的时间复杂度是线性的，为$O(M+N)$

吐槽一句，这个算法的名字的读法，很奇怪，我出去学习的时候老师说应该读tǎ yáng，但是我的学长们说应该对tǎ jiān，不过，我比较喜欢叫它tài jiān，这多接地气。。。。QwQ

Tarjan代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <stack>
#include <cmath>
#define MAXN 100050
#define INF  2147483647

using namespace std;

int n, m, tot;
int u[MAXN], v[MAXN], w[MAXN];
int first[MAXN], next[MAXN];
int dfn[MAXN], low[MAXN];
bool vis[MAXN];
stack<int> S;

void Tarjan(int x) {
    dfn[x] = low[x] = ++tot;
    S.push(x);
    vis[x] = 1;
    int k = first[x];
    while(k != -1) {
        if(!dfn[v[k]]) {
            Tarjan(v[k]);
            low[x] = min(low[x], low[v[k]]);
        }
        else if(vis[v[k]] == 1&&dfn[v[k]]) {
            low[x] = min(low[x], low[v[k]]);
        }
        k = next[k];
    }
    if(dfn[x] == low[x]) {
        while(!S.empty()) {
            int temp = S.top();
            S.pop();
            printf("%d ", temp);
            vis[temp] = 0;
            if(temp == x) break;
        }
        printf("
");
    }
    return ;
}

int main() {
    scanf("%d%d", &n, &m);
    memset(first, -1, sizeof(first));
    for(int i=1; i<=m; i++) {
        scanf("%d%d", &u[i], &v[i]);
        w[i] = 1;
        next[i] = first[u[i]];
        first[u[i]] = i;
    }
    for(int i=1; i<=n; i++)
        if(!dfn[i])
            Tarjan(i);
    return 0;
}

　　

附赠大家一组样例

Sample Input

6 8
1 3
1 2
2 4
3 4
3 5
4 6
4 1
5 6

　　

Sample Output

6
5
3 4 2 1