Luogu P1514 引水入城

题目描述

在一个遥远的国度，一侧是风景秀美的湖泊，另一侧则是漫无边际的沙漠。该国的行政区划十分特殊，刚好构成一个 (N) 行 ( imes M) 列的矩形，如上图所示，其中每个格子都代表一座城市，每座城市都有一个海拔高度。

为了使居民们都尽可能饮用到清澈的湖水，现在要在某些城市建造水利设施。水利设施有两种，分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。

因此，只有与湖泊毗邻的第(1)行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差，将湖水从高处向低处输送。故一座城市能建造输水站的前提，是存在比它海拔更高且拥有公共边的相邻城市，已经建有水利设施。由于第 (N) 行的城市靠近沙漠，是该国的干旱区，所以要求其中的每座城市都建有水利设施。那么，这个要求能否满足呢？如果能，请计算最少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。

输入样例#1

2 5
9 1 5 4 3
8 7 6 1 2

输出样例#1

1
1

输入样例#2

3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2

输出样例#2

1
3

说明

【样例1 说明】

只需要在海拔为 99 的那座城市中建造蓄水厂，即可满足要求。

【样例2 说明】

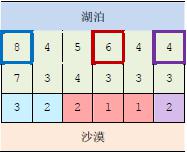
上图中，在 3 3 个粗线框出的城市中建造蓄水厂，可以满足要求。以这 3 3 个蓄水厂为源头在干旱区中建造的输水站分别用3 种颜色标出。当然，建造方法可能不唯一。

数据范围

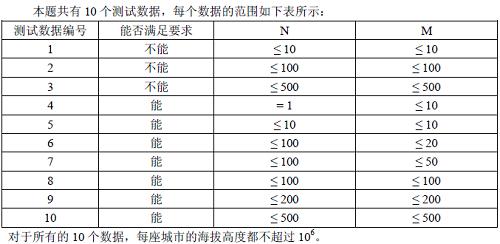
思路

乍一看貌似只能打暴力，于是不顾一切的开始淦
但是结果很感人啊

后来想起来，之前学姐讲过这个题。
但是当时并没有好好听课，so还是不会，我就开始想啊
好像是要用贪心来啊
但是咋贪是个问题
于是我继续看题目
最下面的图片让我记起来了咋做

---

我们先用一个普通的(DFS)来判断第(N)行的所有点能否引水入城在确定能够满足题目要求之后
我们来想一下。这样的一张满足要求的图，第一行的每一个点的水所能流到的最后一行的点必然是一个区间
为什么？

我可以告诉你我不知道啦啦啦啦

那么将第一行每一个点能够放水的城市就可以用BFS变成了一个区间，然后做一个区间覆盖就能得出答案了

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#include <algorithm>

const int maxn = 503;

using namespace std;

int n, m, h[maxn][maxn], nownode, Ans, tot;
bool vis[maxn][maxn], book[maxn], hhh;
int dx[6] = {1, 0, -1, 0};
int dy[6] = {0, 1, 0, -1};

struct edge {
	int l, r;
}ed[maxn];
struct node {
	int x, y;
};

queue<node> Q;

bool cmp(edge a, edge b) {
	if(a.l != b.l) return a.l < b.l;
	return a.r > b.r;
}

void BFS(node now) {
	while(!Q.empty()) {
		now = Q.front();
		Q.pop();
		int x = now.x, y = now.y;
		if(x == n) {
			ed[nownode].l = min(ed[nownode].l, y);
			ed[nownode].r = max(ed[nownode].r, y);
		}
		for(int i=0; i<4; i++) {
			int xx = dx[i]+x, yy = dy[i]+y;
			if(!vis[xx][yy] && xx <= n && xx > 0 && yy <= m && yy > 0 && h[xx][yy] < h[x][y]) {
				Q.push((node) {xx, yy});
				vis[xx][yy] = 1;
			}
		}
	}
}

void dfs(int x, int y) {
	if(x == n) {
		++tot;
	}
	for(int i=0; i<4; i++) {
		int xx = dx[i]+x, yy = dy[i]+y;
		if(h[xx][yy] < h[x][y] && !vis[xx][yy] && xx > 0 && yy > 0 && xx <= n && yy <= m) {
			vis[xx][yy] = 1;
			dfs(xx, yy);
		}
	}
}

int main() {
	scanf("%d%d", &n, &m);
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=m; j++) {
			scanf("%d", &h[i][j]);
		}
	}
	for(int i=1; i<=m; i++) {
		dfs(1, i);
	}
	if(tot < m) {
		printf("0
%d", m-tot);
		return 0;
	}
	for(int i=1; i<=m; i++) {
		nownode = i;
		ed[nownode].l = 2147483647;
		ed[nownode].r = 0;
		while (!Q.empty()) Q.pop();
		memset(vis, 0, sizeof(vis));
		vis[1][i] = 1;
		Q.push((node) {1, i});
		BFS(Q.front());
	}
	sort(ed+1, ed+1+m, cmp);
	int cur = 0, nur = 0;
	Ans = 0;
	for(int i=1; i<=m; i++) {
		if(ed[i].l > m) break;
		if(ed[i].l <= cur+1)
			nur = max(ed[i].r, nur);
		else {
			cur = nur;
			Ans++;
			nur = max(nur, ed[i].r);
		}
	}
	if(cur != m) Ans++;
	printf("1
%d", Ans);
	return 0;
}