图解Java数据结构之环形链表

本篇文章介绍数据结构中的环形链表。

介绍

环形链表，类似于单链表，也是一种链式存储结构，环形链表由单链表演化过来。单链表的最后一个结点的链域指向NULL，而环形链表的建立，不要专门的头结点，让最后一个结点的链域指向链表结点。 简单点说链表首位相连，组成环状数据结构。如下图结构：

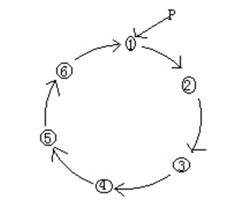
而在环形链表中，最为著名的即是约瑟夫环问题。

约瑟夫环问题

问题介绍：
设编号为1、2、3、... 、n的n个人围坐一圈，约定编号为k(1<=k<=n)的人从1开始报数，数到m的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列。依次类推，直到所有人出列为止，由此产生一个出队编号的序列。
我们可以举个例子来分析一下：
假设一共有5个人，即n = 5；从第一个人开始报数，即k = 1；数到2的人出列，即m = 2。
示意图如下：

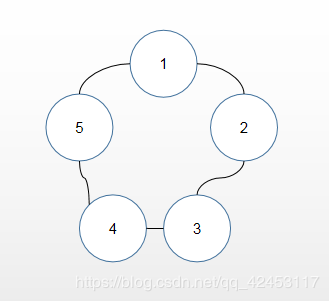
出队列的顺序即为：2 -> 4 -> 1 -> 5 -> 3

那么我们首先得构建出一个单向的环形链表。

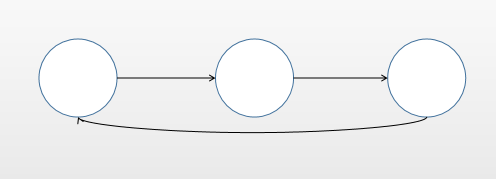
实现分析：

1. 先创建第一个节点，让first指向该节点，并形成环状
2. 每创建一个新的节点就将该节点加入到已有的环形链表中

分析完毕，我们用代码实现一下：

//创建一个环形的单向链表
class CircleSingleLinkedList {
	// 创建一个first节点，当前没有编号
	private Boy first = null;

	// 添加节点，构建成一个环形链表
	public void addBoy(int nums) {
		// 对nums做一个校验
		if (nums < 1) {
			System.out.println("数据错误");
			return;
		}

		// 定义辅助节点
		Boy curBoy = null;

		// 使用循环创建环形链表
		for (int i = 1; i <= nums; i++) {
			// 根据编号创建节点
			Boy boy = new Boy(i);
			// 如果是第一个节点
			if (i == 1) {
				first = boy;
				first.setNext(first);
				curBoy = first;// 让curBoy指向第一个节点，帮助构建链表
			} else {
				curBoy.setNext(boy);
				boy.setNext(first);// 使其指向第一个节点，形成环状
				curBoy = boy;// curBoy后移
			}
		}
	}

	// 遍历当前环形链表
	public void list() {
		// 判断链表是否空
		if (first == null) {
			System.out.println("链表为空");
			return;
		}
		// 定义辅助节点
		Boy curBoy = first;
		while (true) {
			System.out.println("节点编号:" + curBoy.getNo());
			if (curBoy.getNext() == first) {
				// 此时说明遍历完毕
				break;
			}
			curBoy = curBoy.getNext();// curBoy后移
		}
	}
}

//创建一个Boy类，表示一个节点
class Boy {
	private int no;// 编号
	private Boy next;// 指向下一个节点

	public Boy(int no) {
		this.no = no;
	}

	public int getNo() {
		return no;
	}

	public void setNo(int no) {
		this.no = no;
	}

	public Boy getNext() {
		return next;
	}

	public void setNext(Boy next) {
		this.next = next;
	}
}

这样就实现了一个环形链表，接下来测试一下：

public static void main(String[] args) {
		CircleSingleLinkedList circleSingleLinkedList = new CircleSingleLinkedList();
		circleSingleLinkedList.addBoy(5);
		circleSingleLinkedList.list();
}

运行结果：

节点编号:1
节点编号:2
节点编号:3
节点编号:4
节点编号:5

运行结果也是没有问题的，接下来便是生成出圈序列。
问题分析：

1. 先创建一个辅助节点helper，事先应该指向环形链表的最后一个节点
2. 报数前，先让first和helper移动k - 1次
3. 开始报数时，让first和helper节点同时移动，移动m - 1次
4. 此时可以将first指向的节点出圈
5. 如何出圈呢?
   使first = first.next，即：将first节点往前移动一下
   使helper.next = first，这样就跳过了要出圈的节点

接下来是代码实现：

	/**
	 * 根据用户的输入，计算出圈序列
	 * 
	 * @param startNo  表示从第几个开始数
	 * @param countNum 表示数几下
	 * @param nums     表示一共有多少人
	 */
	public void countBoy(int startNo, int countNum, int nums) {
		// 数据校验
		if (first == null || startNo < 1 || startNo > nums) {
			System.out.println("参数输入有误");
			return;
		}
		// 定义辅助节点
		Boy helper = first;
		// helper事先应该指向环形链表的最后一个节点
		while (true) {
			if (helper.getNext() == first) {
				break;
			}
			helper = helper.getNext();// helper后移
		}
		// 报数前，先让first和helper移动k - 1次
		for (int j = 0; j < startNo - 1; j++) {
			first = first.getNext();
			helper = helper.getNext();
		}
		// 开始报数时，让first和helper节点同时移动，移动m - 1次
		// 这里是一个循环的操作，直到圈中只有一个节点
		while (true) {
			if (helper == first) {
				// 此时说明圈中只有一个人
				break;
			}
			// 让first和helper同时移动countNum - 1次
			for (int j = 0; j < countNum - 1; j++) {
				first = first.getNext();
				helper = helper.getNext();
			}
			// 此时first指向的节点就是要出圈的节点
			System.out.println("节点" + first.getNo() + "出圈");
			// 将该节点出圈
			first = first.getNext();
			helper.setNext(first);
		}
		System.out.println("最后留在圈中的节点编号:" + first.getNo());
	}

这个实现的逻辑相对来说还是比较复杂和难以理解的，接下来编写测试代码：

	public static void main(String[] args) {
		CircleSingleLinkedList circleSingleLinkedList = new CircleSingleLinkedList();
		circleSingleLinkedList.addBoy(5);
		circleSingleLinkedList.list();

		System.out.println("--------------");

		// 测试出圈序列
		circleSingleLinkedList.countBoy(1, 2, 5);
	}

运行结果：

节点编号:1
节点编号:2
节点编号:3
节点编号:4
节点编号:5
--------------
节点2出圈
节点4出圈
节点1出圈
节点5出圈
最后留在圈中的节点编号:3

和开始计算的结果相吻合。
到此，关于约瑟夫环的问题就成功解决了。