浅谈堆-Heap（二）

上节知识复习

• 粗略的分析了堆的几个应用场景

• 用代码实现了一个简易的大顶堆

堆构建及其应用场景-堆排序及其优化

• 堆排序及堆的构建

上一小节我们已经实现了一个大顶堆的元素的插入和最大元素的弹出，有这两个方法，很容易对给定的一系列元素排序，具体方法就是先把这些元素都添加到这个大顶堆中，然后一个一个的弹出放到数组，最后这个数组中的元素就是有序的，为了让其从小到大的排序，我们可以在循环弹出的时候，从数组的最后一个元素向前放置.具体实现如代码

private static void heapSort(Integer[] arr) {
    if (arr == null || arr.length <= 0)
        throw new IllegalArgumentException("arr to sort can't be null");
    //这里采用上一节实现的大顶堆
    MaxHeap<Integer> maxHeap = new MaxHeap<>(Integer.class, arr.length);
    for (Integer s : arr)
        maxHeap.insert(s);
    //依次弹出最大的元素放入到数组中
    for(int i = arr.length - 1 ; i >= 0 ; i--) {
        arr[i] = maxHeap.popMax();
    }
}

写个单元测试，测试随机100W个数据排序,并打印一下耗费时间

public static void main(String[] args) {
    Integer[] arr = new Integer[1000000];
    Random random = new Random();
    for(int i = 0 ; i < 1000000 ; i++) {
        arr[i] = random.nextInt(1000000);
    }
    long start = System.currentTimeMillis();
    heapSort(arr);
    long end = System.currentTimeMillis();
    System.out.println("take: " + (end - start) + " ms");
    Arrays.asList(arr).forEach(System.out::println);
}

多次测试在我本机，耗时从620ms到670ms不等，先来分析一下时间复杂度.

todo:

我们姑且先把这个方法记下，待后面优化后，和归并、快排、多路归并快排、TimSort一起比较不同的数据的排序效率. 但是总感觉哪儿不太对，不能每次排序前，循环一遍给定的元素插入到堆中，再弹出，这效率有点儿低.，有没有一种方法不进行遍历给定的元素，就把给定的元素当成一个堆，只不过这个时候整个堆不满足堆的性质，可以通过特殊的方式调整让其满足大顶堆或者小顶堆的性质.来我们假设给定一堆元素，从前向后标上序号把他们变成一颗完全二叉树, 如图我们直接把给定的数组看成一个完全二叉树.

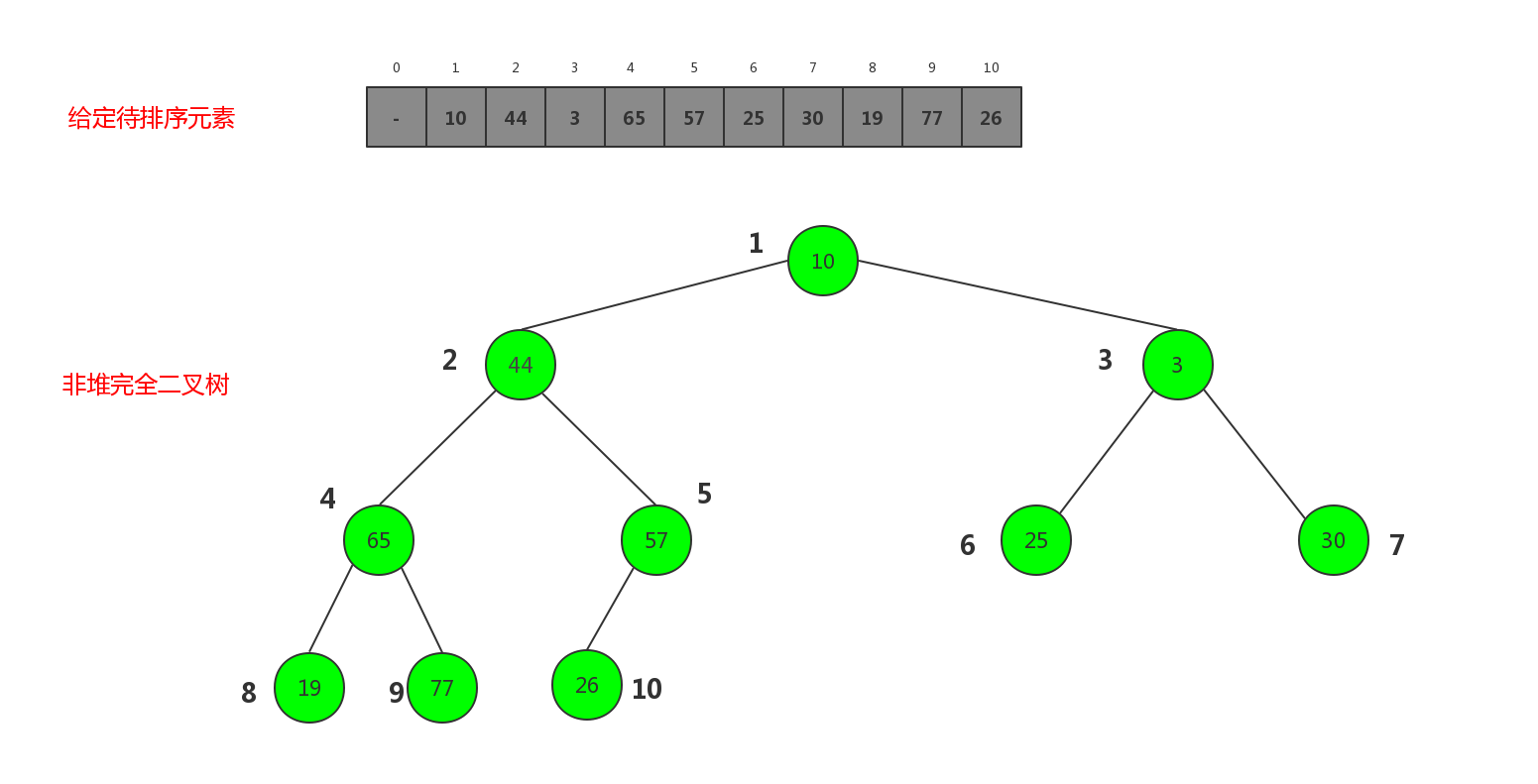
显然这颗完全二叉树既不满足大顶堆的性质，也不满足小顶堆的性质. 但是所有的叶子节点各自都是一个大顶堆或者小顶堆，因为每个叶子节点如 25、30、19、77、26 都可以当做是他们自己为根没有孩子的大顶堆. 这些元素可以暂且不动. 回顾一下上一节，我们在构建堆也就是向堆中插入元素时，插入到最后一个节点，然后进行shiftUp的操作调整使其满足大顶堆的性质. 这里我们一样可以进行类似的操作，但是入口在哪儿呢，仔细观察，既然所有的叶子节点已经满足最大堆的性质，那我们就从第一个不是叶子节点的节点开始， 这里图上是57 这个节点，也就是序号是5的这个节点.怎么找到这个节点呢，试想一下.完全二叉树的性质是最后一层叶子节点是从左至右，不可能出现只有右子节点，没有左子节点的情况，我们的序号又是根据层序从左至右编号的.最后一个叶子节点的父节点一定是第一个非叶子节点.而我们给定节点的序号也是从1开始的，所以最后一个节点的序号index也是给定元素的个数，而其父节点则是 程序上的（8/2 = 4 , 9/2 = 4）index / 2. 即如果给定元素的个数是n，第一个非叶子节点的序号就是 n/2 . 所以我们就可以从第一个非叶子节点开始依次向前 第二个非叶子节点(如上图的 65)直到根节点操作.但是这个操作是 上滤还是下沉呢，显然是下沉. 来我们实现一下代码，只需要增加一个构造方法即可，在构造方法中初始化堆的构建.下面我们给第一个小节中的MaxHeap添加一个构造方法.

todo: