曲率
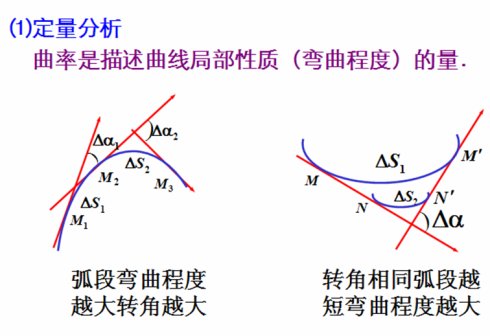
曲率 是衡量弯曲的程度。
曲率的直观感受
方便引入曲率的概念,先从两个特殊的例子来直观上感受曲率
直线
对直线来说,没有弯曲的地方,显然曲率到处都是0。
圆
对圆来说,任何地方的曲率都是相同的,所以圆的曲率是个常数。直观上来看,半径大的圆比半径小的圆更"平直"一些,那么大圆的曲率相比来说就要小一些。
怎么量化圆的曲率呢?
假设圆的半径为R,弧长为$$2 pi R$$,那么曲率=$$frac{2 pi}{2 pi R} = frac{1}{R}$$ 。
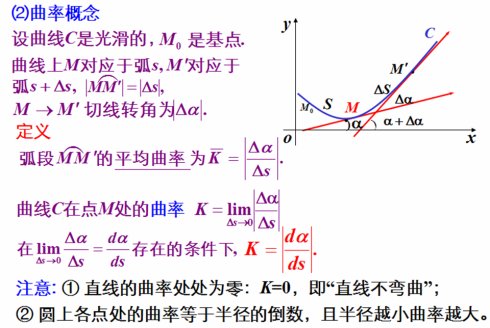
一般化推导
对圆的局部而言,圆的弯曲程度 可以用 切线斜角的变化 与 弧长变化 之商 来表示。
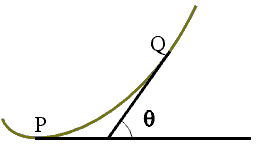
举个例子,

如上图所示,从P点到Q点,切线角的变化量为$$angle POQ$$,弧长的变化为$$widehat{PQ}$$,所以曲率=$$frac{angle POQ}{widehat{PQ}}=frac{ heta}{ heta*R}=frac{1}{R}$$。
对一般曲线而言,
如上图所示,曲线从P点到Q点,切线角的变化量为$$ heta$$,将其除以弧长的变化量$$widehat{PQ}$$,然后让Q逼近P点,
极限值 = $$lim_{Q o P} frac{ heta}{widehat{PQ}}$$,即可得到曲线在P点的曲率。
从这个推到也可以看出,直线的曲率为0,圆的曲率为其半径的倒数。
最后,来两张比较好的图