1.向量——数学定义
-
向量:数学家——数字列表,程序员——数组
-
向量记法
- 向量的维度就是向量包含的 “数” 的数目,标量可以被认为是一维向量
- 数学中常使用整数下标表示某个向量的分量,如 (V_1) 表示向量 (V) 的第一个元素。这里只讨论 2D、3D、4D 向量,不涉及 n 维向量,所以采用 x,y 代表 2D 向量的分量;x,y,z 代表 3D 向量的分量;x,y,z,w 代表 4D 向量的分量
2.向量——几何定义
-
从几何意义上说,向量是有大小和方向的有向线段(并不包括起始位置)
-
位置与位移
- 向量没有位置,只有大小和方向,例如,“向前走三步”,“以50英里每小时的速度向北行驶”
- 因为向量能描述事物间的位移和相对差异,所以它能用来描述相对位置
- 因为向量是没有位置的,所以能在图中的任何地方表示,只要方向和长度的表示正确即可。可以利用向量这个优点,将向量平移到图中更有用的点
-
用一系列数(数组)表示向量
-
向量中的数表达了向量在每个维度上的有向位移。例如,2D 向量 [x,y] 列出的是沿 x 坐标方向和 y 坐标方向的位移
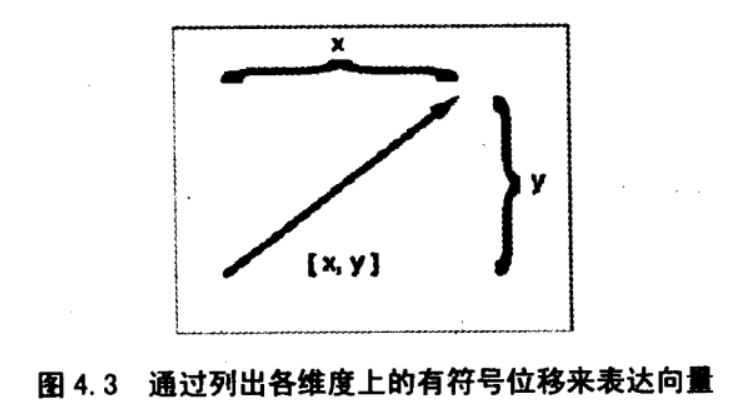
-
-
用一系列位移表示向量
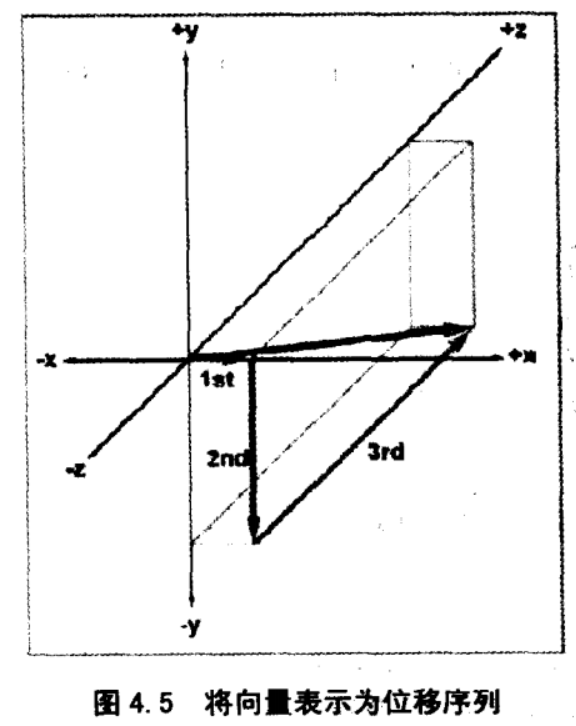
- 为了理解向量所代表的位移,可以将向量分解成与轴平行的分量,把这些分量的位移组合起来,就得到了向量作为整体所代表的位移。例如,3D 向量 [1,-3,4] 表示的一个单一的位移,可以分解为向右平移一个单元,向下平移3个单元,向前平移4个单元(假设 +x,+y,+z 轴分别向右,向上,向前)
- 这些步骤的执行顺序无关紧要,不同的顺序对应着向量轴对齐包围盒上的不同路径
3.向量与点
-
使用 “点” 和 “向量” 的墓地完全不同,“点” 描述位置,而 “向量” 描述位移
- 下图坐标展示一个点的位置,右图展示一个向量,可以看到点和向量之间有某种联系
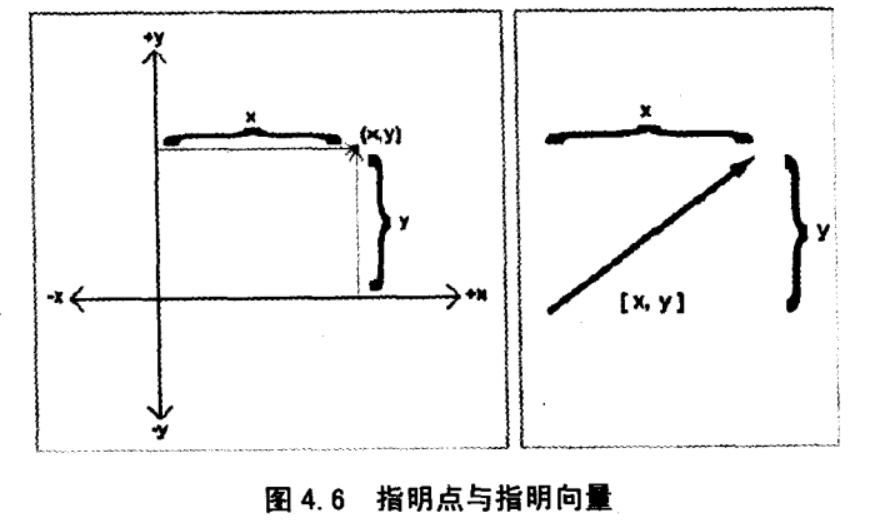
-
相对位置
- 上面说到,向量能够描述相对位置,而相对位置:某个物体的位置,通过描述它与已知点之间的相对关系来指明。那么在描述一个点的位置时,总是要描述它和其他一些点的关系,任何对于位置的描述只有在一定参考系内才有意义
-
点和向量的关系
-
如下图所见,点和向量的关系可以描述为:从原点开始,按向量 [x,y] 所代表的位移移动,总是会到达点(x,y)所代表的位置。也可以说,向量 [x,y] 描述了原点到点(x,y)的位移量
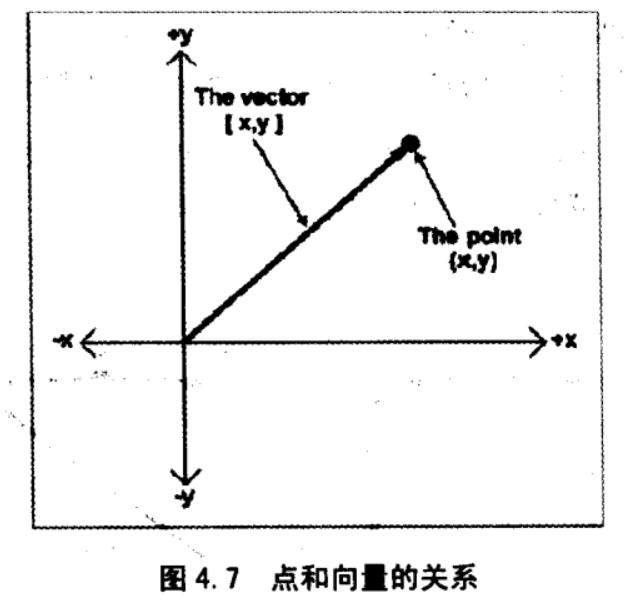
-
点和向量在概念是不同的,但在数学上是等价的。思考位置时,想象一个点,思考位移时,想象一个向量和箭头
-