opencv —— HoughLines、HoughLinesP 霍夫线变换原理（标准霍夫线变换、多尺度霍夫线变换、累积概率霍夫线变换）及直线检测

霍夫线变换的原理

• 一条直线在图像二维空间可由两个变量表示，有以下两种情况：

① 在笛卡尔坐标系中：可由参数斜率和截距（k，b）表示。

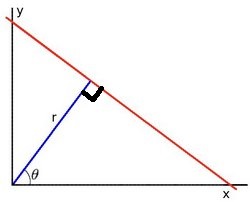
② 在极坐标系中：可由参数极经和极角（r，θ）表示。

对于霍夫线变换，我们将采用第二种方式极坐标系来表示直线，因此直线的表达式可为：

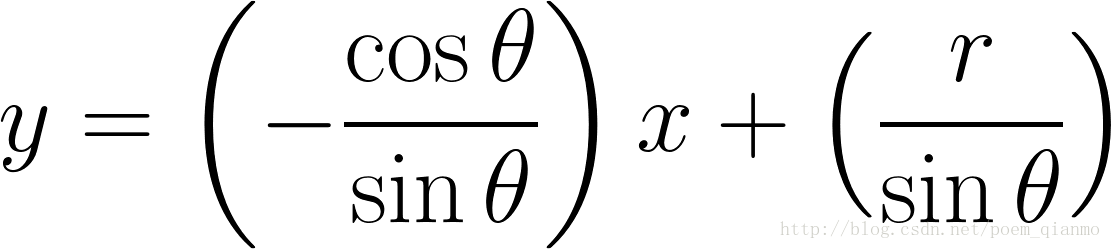
化简便可得到：

• 对于（x₀，y₀），我们可以将通过这一点的所有直线统一定义为：

这就意味着每一对 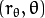 代表一条通过点  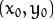的直线。 

• 对于一个给定点 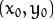  ，我们可以在直角坐标系中，绘出所有通过它的直线（θ 为 x 轴，r 为 y 轴）。最终我们将得到一条正弦曲线。

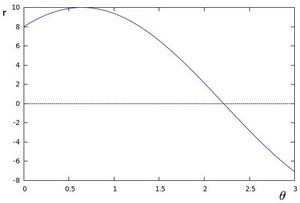
注意：只绘出满足下列条件的点 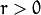  and  。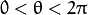

• 我们可以对图像中所有的点进行上述操作.。如果两个不同点进行上述操作后得到的曲线在平面 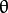 -  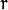相交, 这就意味着它们有一个公共的（θ，r_θ），即过一条公共的直线。下图中，若曲线每点权重均为 1 ，则交点处权重为 3。

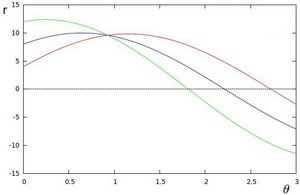
• 越多曲线交于一点，也就意味着这个交点表示的直线由更多的点组成，权重和越大。我们可以设置一个阈值，来决定多少条曲线交于一点（权重多大）我们才认为检测到了一条直线。

• 这就是霍夫线变换要做的.。它追踪图像中每个点对应曲线间的交点.。如果交于一点的曲线的数量超过了阈值, 那么可以认为这个交点所代表的参数对 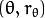   在原图像中为一条直线。

OpenCV 实现了以下三种霍夫线变换：

1. 标准霍夫变换（StandardHough Transform，SHT）
   • 原理在上面的部分已经说明了. 它能给我们提供一组参数对（ρ，θ）的集合来表示检测到的直线。
   • 在 OpenCV 中通过函数 HoughLines 来实现。
2. 多尺度霍夫变换（Multi-ScaleHough Transform，MSHT）
   • 和标准霍夫变换类似。
3. 累计概率霍夫变换（ProgressiveProbabilistic Hough Transform，PPHT），由HoughLinesP函数调用。
   • 这是执行起来效率更高的霍夫线变换. 它输出检测到的直线的端点 。
   • 在 OpenCV 中它通过函数 HoughLinesP 来实现。

 

标准 & 多尺度 霍夫线变换：HoughLines 函数

void HoughLines(InputArray image, OutputArray lines, double rho, double theta, int threshold, double srn = 0, double stn = 0);

• image，输入图像，即源图像。需要为 8 位的单通道二值图像。
• lines，存放直线的矢量信息的数组。每条直线由具有 2 个元素的矢量（ρ，Θ）表示，其中，ρ 是离坐标原点（0，0）也就是图像左上角的距离，Θ 是弧度线条旋转角度（0 表示垂直直线，∏/2 表示水平直线，注意，不是 0 度和 90 度）                                                          
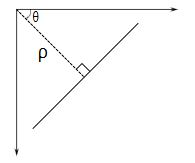
• rho，以像素为单位的距离精度。另一种表述是平面 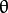 -  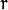中 r 轴的单位长度。
• theta，以弧度为单位的角度精度。另一种表示是平面 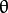 -  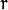中 θ 轴的单位长度。
• threshold，权重累加平面的阈值参数。大于阈值 threshold 的线段才可以被确认为直线。
• srn，默认值为 0。多尺度霍夫线变换才会用到的参数。对于多尺度霍夫线变换，平面 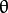 -  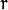中 r 轴的单位长度 = rho / srn。
• stn，默认值为 0。也是多尺度霍夫线变换才会用到的参数。对于多尺度霍夫线变换，平面 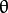 -  中 θ 轴的单位长度 = theta / stn。如果 srn、stn 同时为 0，就表示使用经典霍夫变换，否则两个参数都应该为正数。

 

代码示例：

#include<opencv.hpp>
#include<iostream>
using namespace std;
using namespace cv;
int hough_value = 70;
Mat src, canny_img;
void hough_change(int, void*) {
    vector<Vec2f>lines;
    HoughLines(canny_img, lines, 1, CV_PI / 180.0, hough_value);
    RNG rngs = { 12345 };
    Mat show = src.clone();
    for (int i = 0; i < lines.size(); i++) {
        float rho = lines[i][0], theta = lines[i][1];

        double sin_theta = sin(theta), cos_theta = cos(theta);
        double x = rho * cos_theta, y = rho * sin_theta;

        //以垂点为基础，将直线延长
        Point pt1, pt2;
        pt1.x = cvRound(x + 1000 * (-sin_theta));
        pt1.y = cvRound(y + 1000 * (cos_theta));
        pt2.x = cvRound(x - 1000 * (-sin_theta));
        pt2.y = cvRound(y - 1000 * (cos_theta));

        Scalar colors = Scalar(rngs.uniform(0, 255), rngs.uniform(0, 255), rngs.uniform(0, 255));
        line(show, pt1, pt2, colors, 2);
    }
    imshow("show", show);
}
int main() {
    src = imread("C:/Users/齐明洋/Desktop/1.jpg");
    GaussianBlur(src, src, Size(3, 3), 0, 0);
    imshow("src", src);

    Canny(src, canny_img, 55, 110, 3);
    imshow("canny_img", canny_img);

    namedWindow("show");
    createTrackbar("threshold", "show", &hough_value, 200, hough_change);
    hough_change(0, 0);

    waitKey(0);
}

效果演示：

 

 

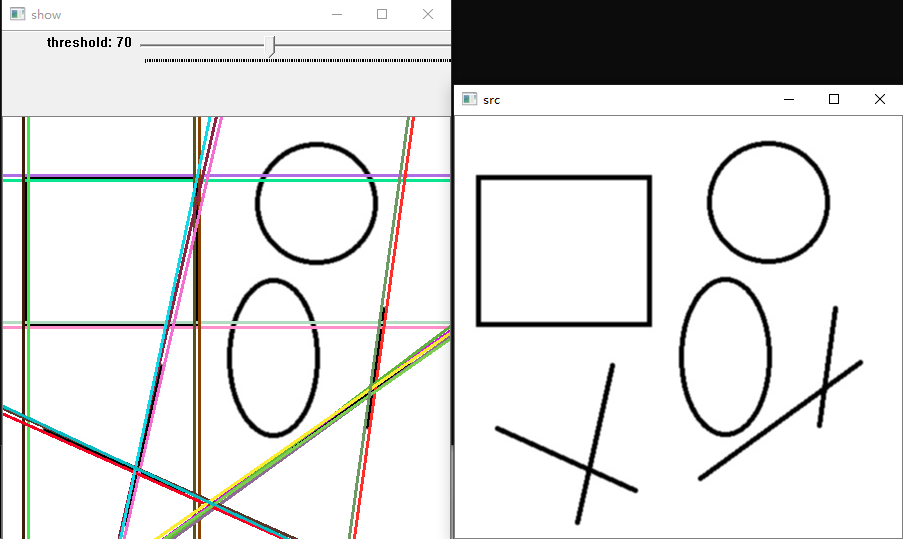
累计概率霍夫变换：HoughLinesP 函数

void HoughLinesP(InputArray image, OutputArray lines, double rho, double theta, int threshold, double minLineLength = 0, double maxLineGap= 0);

• lines，存放直线信息矢量的数组。每条直线由具有 4 个元素的矢量（x_1，y_1，x_2，y_2）表示，其中，（x_1，y_1）和（x_2，y_2）是每条检测到的直线的两端端点。
• minLineLength ，默认值为 0。最短线段的长度，比这个设定参数短的线段就不能被显现出来。
• maxLineGap，默认值为 0。允许将同一行点与点之间连接起来的最大距离。
• 其余参数，类比 HoughLines 函数的参数。

 

代码示例：

#include<opencv.hpp>
#include<iostream>
using namespace std;
using namespace cv;
int hough_value = 70;
Mat src, canny_img;
void hough_change(int, void*) {
    vector<Vec4f>lines;
    HoughLinesP(canny_img, lines, 1, CV_PI / 180, hough_value, 10, 5);
    RNG rngs = { 12345 };
    Mat show = src.clone();
    for (int i = 0; i < lines.size(); i++) {
        Point pt1, pt2;
        pt1.x = lines[i][0];
        pt1.y = lines[i][1];
        pt2.x = lines[i][2];
        pt2.y = lines[i][3];

        Scalar colors = Scalar(rngs.uniform(0, 255), rngs.uniform(0, 255), rngs.uniform(0, 255));
        line(show, pt1, pt2, colors, 2);
    }
    imshow("show", show);
}
int main() {
    src = imread("C:/Users/齐明洋/Desktop/1.jpg");
    GaussianBlur(src, src, Size(3, 3), 0, 0);
    imshow("src", src);

    Canny(src, canny_img, 55, 110, 3);
    imshow("canny_img", canny_img);

    namedWindow("show");
    createTrackbar("threshold", "show", &hough_value, 200, hough_change);
    hough_change(0, 0);

    waitKey(0);
}

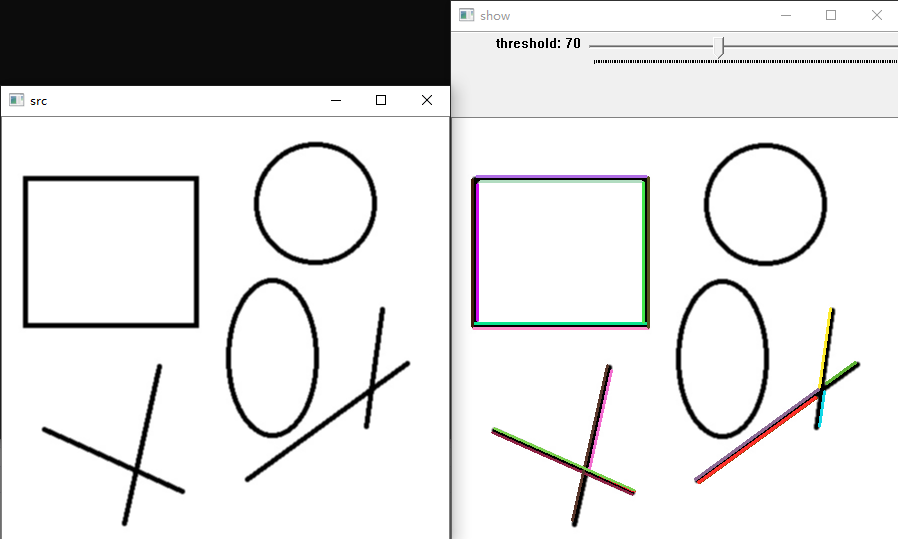
效果演示：

 

借鉴博客：https://www.cnblogs.com/xmu-rcs-jty/p/7531814.html

http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/imgproc/imgtrans/hough_lines/hough_lines.html