一、决策树
1.1、概述
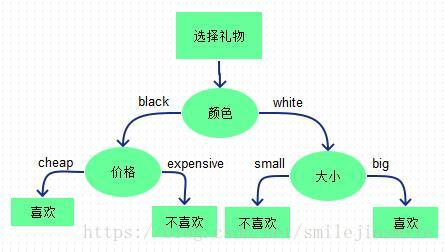
if, else if, else,其实就就是决策树的思想。 只是这么多条件，哪个条件特征先做if，哪个条件特征后做if比较优呢？怎么准确定量选择这个标准就是决策树算法的要做的事情。
准备，补充两个对数去处公式：
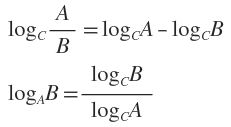
1.2、信息论中的熵
熵度量了事物的不确定性，越不确定的事物，它的熵就越大。熵是无序性（或不确定性）的度量指标。具体的，随机变量X的熵的表达式如下：
单随机变量 X 的熵
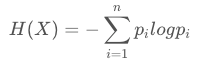通常以2为底数，所以信息熵的单位是bit。
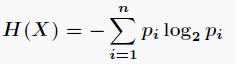既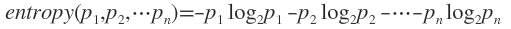
双变量 X和Y 的联合熵
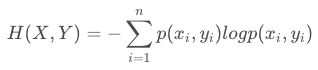
条件熵的表达式H(X|Y)，条件熵类似于条件概率,它度量了我们的X在知道Y以后剩下的不确定性。表达式如下：
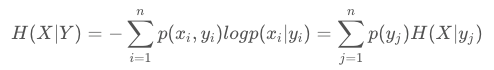
根据决策树构建的过程，可以按照特征选择方式分成如下三种大类：
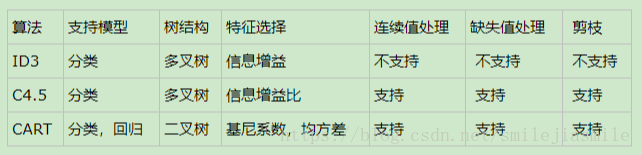
信息增益(又称为互信息),定义为： H(X) - H(X|Y) ,记为I(X,Y)。
1.2.1、ID3
在决策树 ID3 算法中叫做信息增益。ID3算法就是用信息增益来判断当前节点应该用什么特征来构建决策树。信息增益大，则越适合用来分类。
ID3 的缺点：
没有考虑连续特征，比如长度，密度都是连续值，无法在ID3运用。
取值比较多的特征比取值少的特征信息增益大。
ID3算法对于缺失值的情况没有做考虑等
没有考虑过拟合的问题
详细参看【后期细看】：https://www.cnblogs.com/zhangchaoyang/articles/2196631.html
1.2.2、C4.5
对于使用信息增益作为标准容易偏向于取值较多的特征的问题。引入一个信息增益率的变量Ir(X,Y)，它是信息增益和特征熵的比值。表达式如下：
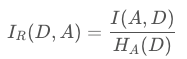
C4.5 的缺点：
决策树算法非常容易过拟合
C4.5生成的是多叉树，在计算机科学中二叉树往往运算效率更高。
C4.5只能用于分类，如果能将决策树用于回归的话可以扩大它的使用范围。
C4.5由于使用了熵模型，里面有大量的耗时的对数运算,如果是连续值还有大量的排序运算。是否可以通过适当的降低结果准确性来简化模型的运算强度。
详细参看【后期细看】：https://www.cnblogs.com/zhangchaoyang/articles/2842490.html
1.2.3、CART
前面两种方式都是基于信息论的熵模型，有耗时的计算问题，CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的。(其实就是加了一个负号，对比信息熵的定义)
在分类问题中，假设有K个类别，第k个类别的概率为pk, 则基尼系数的表达式为：
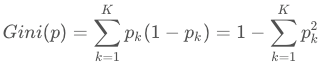
如果是二类分类问题，概率是p，则基尼系数简化为：Gini(p)=2p(1−p)
详细参看【后期细看】：https://www.cnblogs.com/zhangchaoyang/articles/2709922.html
参看原文：
https://blog.csdn.net/smilejiasmile/article/details/82843278