栈模拟非递归算法
递归算法的本质是利用函数的调用栈进行,实际上我们可以自行使用栈来进行模拟,这样的算法空间复杂度为O(h),h为二叉树的高度。
前序遍历
首先把根节点入栈,然后在每次循环中执行以下操作:
- 此时栈顶元素即为当前的根节点,弹出并打印当前的根节点。
- 把当前根节点的右儿子和左儿子分别入栈(注意是右儿子先入栈左儿子后入栈,这样的话下次出栈的元素才是左儿子,这样才符合前序遍历的顺序要求:根节点->左儿子->右儿子)。
后序遍历
因为后序遍历的顺序是:左子树->右子树->根节点,于是我们在前序遍历的代码中,当访问完当前节点后,先把当前节点的左子树入栈,再把右子树入栈,这样最终得到的顺序为:根节点->右子树->左子树,刚好是后序遍历倒过来的版本,于是把这个结果做一次翻转即为真正的后序遍历。而翻转可以通过使用另外一个栈简单完成,这样的代价是需要两个栈,但就复杂度而言,空间复杂度仍然是O(h)。
中序遍历
中序遍历稍微复杂,使用一个指针p指向下一个待访问的节点,p初始化为根节点。在每次循环中执行以下操作:
- 如果p非空,则把p入栈,p变为p的左儿子。
- 如果p为空,说明已经向左走到尽头了,弹出当前栈顶元素,进行访问,并把p更新为其右儿子。
下面是代码实现。
1 # coding:utf-8
2
3 '''
4 递归算法的本质是利用函数的调用栈进行,实际上我们可以自行使用栈来进行模拟,这样的算法空间复杂度为O(h),h为二叉树的高度。
5
6 前序遍历
7 首先把根节点入栈,然后在每次循环中执行以下操作:
8 此时栈顶元素即为当前的根节点,弹出并打印当前的根节点。
9 把当前根节点的右儿子和左儿子分别入栈(注意是右儿子先入栈左儿子后入栈,这样的话下次出栈的元素才是左儿子,
10 这样才符合前序遍历的顺序要求:根节点->左儿子->右儿子)。
11 下面是代码实现。
12
13
14 后序遍历
15 因为后序遍历的顺序是:左子树->右子树->根节点,于是我们在前序遍历的代码中,当访问完当前节点后,先把当
16 前节点的左子树入栈,再把右子树入栈,这样最终得到的顺序为:根节点->右子树->左子树,刚好是后序遍历倒过
17 来的版本,于是把这个结果做一次翻转即为真正的后序遍历。而翻转可以通过使用另外一个栈简单完成,这样的代
18 价是需要两个栈,但就复杂度而言,空间复杂度仍然是O(h)。
19
20
21 中序遍历
22 中序遍历稍微复杂,使用一个指针p指向下一个待访问的节点,p初始化为根节点。在每次循环中执行以下操作:
23 如果p非空,则把p入栈,p变为p的左儿子。
24 如果p为空,说明已经向左走到尽头了,弹出当前栈顶元素,进行访问,并把p更新为其右儿子。
25 '''
26 from random import randint
27
28 class Node(object):
29 def __init__(self, x):
30 self.x = x
31 self.left = None
32 self.right = None
33
34 def PreOrder(root):
35 if not root:
36 return None
37
38 st = [root] # 辅助栈
39 path = [] # 遍历路径
40 while st:
41 node = st.pop()
42 path.append(node.x)
43 if node.right:
44 st.append(node.right)
45 if node.left:
46 st.append(node.left)
47 return path
48
49 def PostOrder(root):
50 if not root:
51 return None
52
53 st = [root]
54 path = []
55 while st:
56 node = st.pop()
57 path.append(node.x)
58 if node.left:
59 st.append(node.left)
60 if node.right:
61 st.append(node.right)
62 return path[::-1] # path值为:根节点->右子树->左子树,所以作一次倒序刚好就是返回结果!
63
64 def InOrder(root):
65 if not root:
66 return None
67 tmp = root; st = []
68 path = []
69 while tmp or st:
70 if tmp:
71 st.append(tmp)
72 tmp = tmp.left
73 else:
74 tmp = st.pop()
75 path.append(tmp.x)
76 tmp = tmp.right
77
78 return path
79
80 def Hierarchy(root):
81 # write code here
82 from collections import deque
83 #if root is None:
84 # return None
85 if not root:
86 return []
87
88 q = deque()
89 q.append(root)
90 ret = []
91 while len(q) > 0:
92 node = q.popleft()
93 ret.append(node.x)
94 if node.left:
95 q.append(node.left)
96 if node.right:
97 q.append(node.right)
98 #q.append(node.right) if node.right else pass
99 return ret
100
101 root = Node(1)
102 root.left = Node(2);root.right = Node(3)
103 root.left.left = Node(4); root.left.right = Node(5)
104 root.right.left = Node(6); root.right.right = Node(7)
105 root.left.left.right = Node(8); root.right.left.right = Node(9)
106 print PreOrder(root)
107 print PostOrder(root)
108 print InOrder(root)
109 print Hierarchy(root)
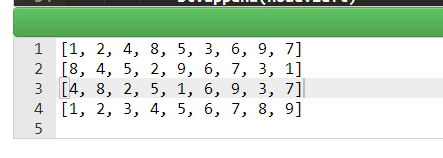
运行结果,树木结构如下:
1
/
2 3
/ /
4 5 6 7
8 9
参考文献:
http://noalgo.info/832.html (大神博客啊)