异常检测
1.1 问题动机 problem motivation
在机器学习中有一个常见的应用就是异常检测问题(Anomaly detection),主要应用在无监督学习上,当然,有时候也会应用在监督学习上
举例: 当飞机引擎从生产线上流出时需要进行QA(质量控制测试),数据集包含引擎的一些特征变量,比如运转时产生的热量,或者振动等。当有一个新的飞机引擎从生产线上流出,它具有特征变量 xtest 。异常检测问题就是:希望知道这个新的飞机引擎是否有某种异常
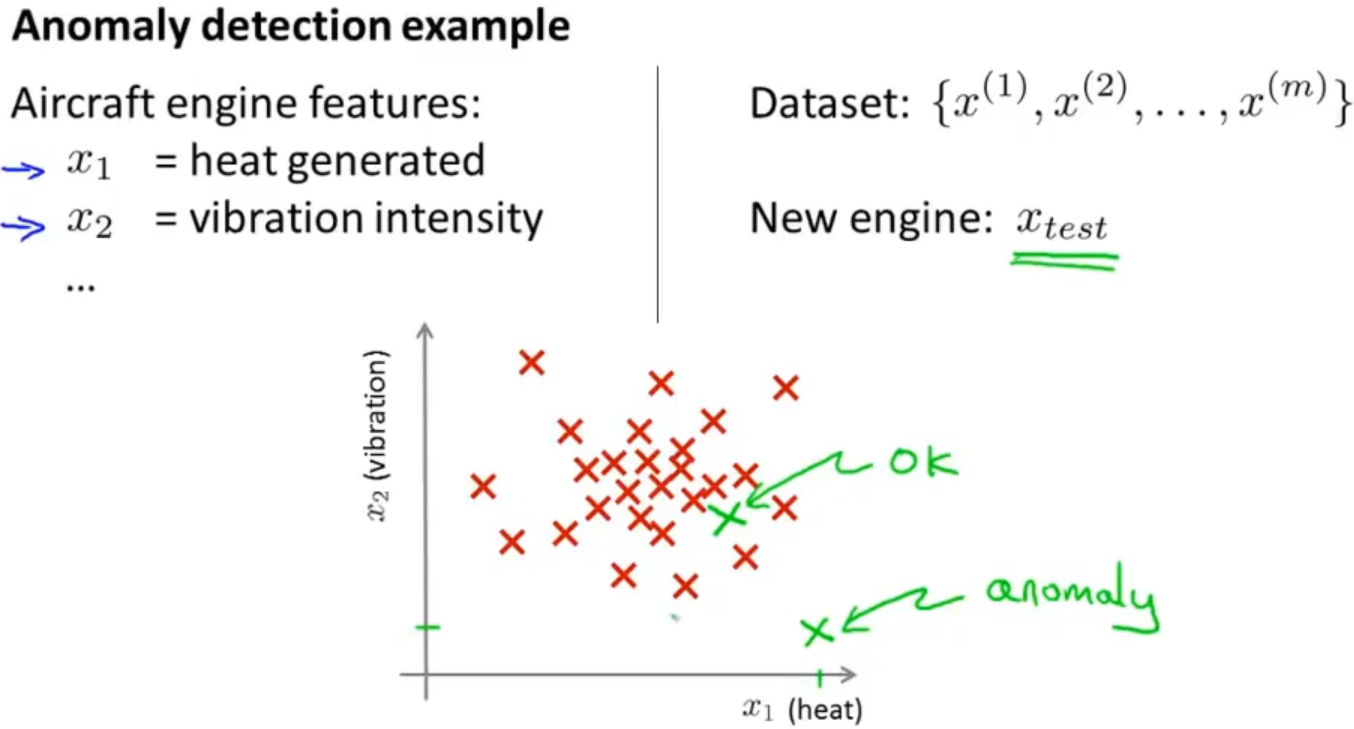
检测的方法是通过训练出的模型,根据 xtest 的位置告诉我们其属于正常数据组的可能性 p(xtest)
采用密度估计的方法来检测,公式被定义为: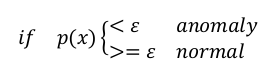
如下图,蓝色圈内的数据属于正常数据组的可能性较高;而越偏远,属于该数据组的可能性就越低

除了飞机引擎的例子,还有一些常见的检测异常例子
比如:
诈骗检测:在线采集的用户数据,特征可能包含:用户多久登录一次,访问过的页面,在论坛发布的帖子数量,甚至是打字速度等。根据这些特征构建模型,用来识别非法的用户
数据中心检测:特征可能包含:内存使用情况,被访问的磁盘数量,CPU 的负载,网络的通信量等。根据这些特征构建模型,用来判断某些计算机是否可能出错了

1.2 高斯分布 Gaussian distribution
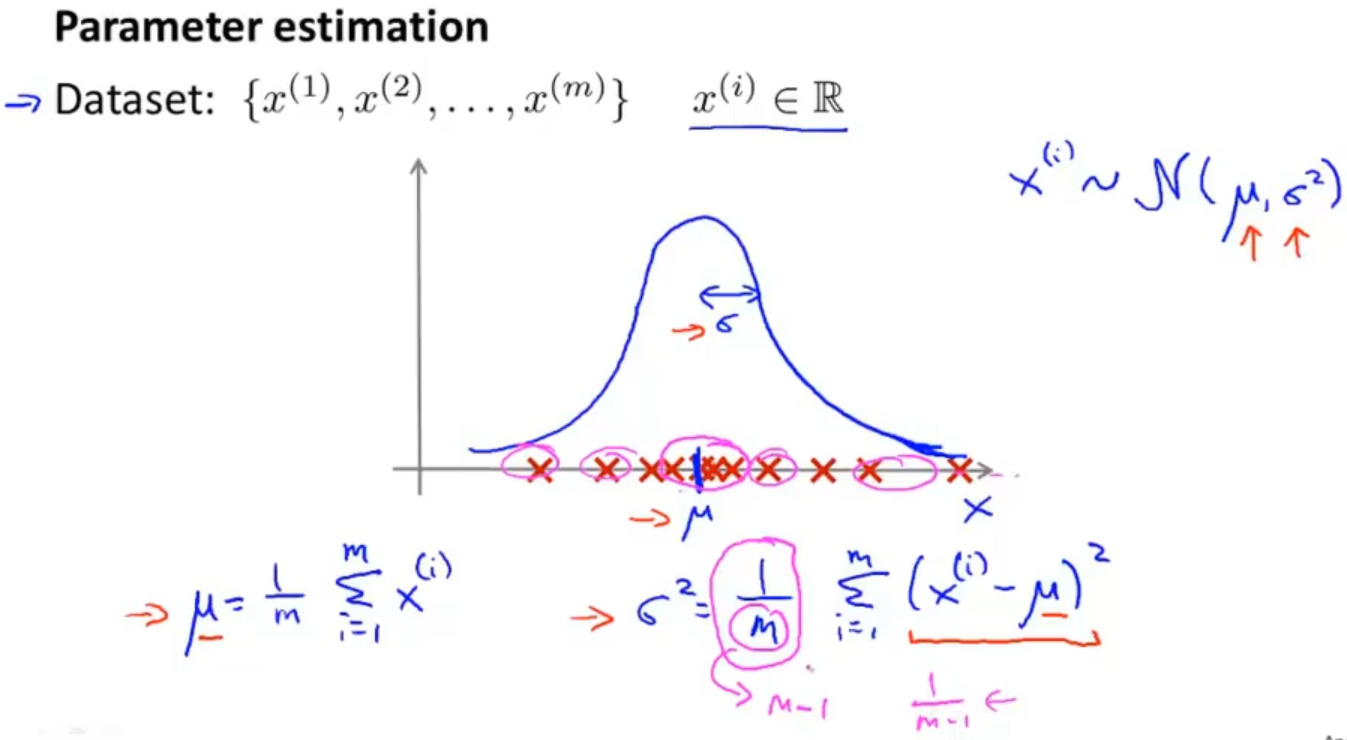
高斯分布也称为正态分布,它有两个参数分别是均值 μ 和方差 σ2 ,通常如果变量 x 符合高斯分布 x∼N(μ, σ2 ) 则其概率密度函数为 :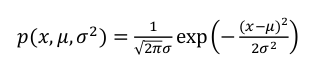
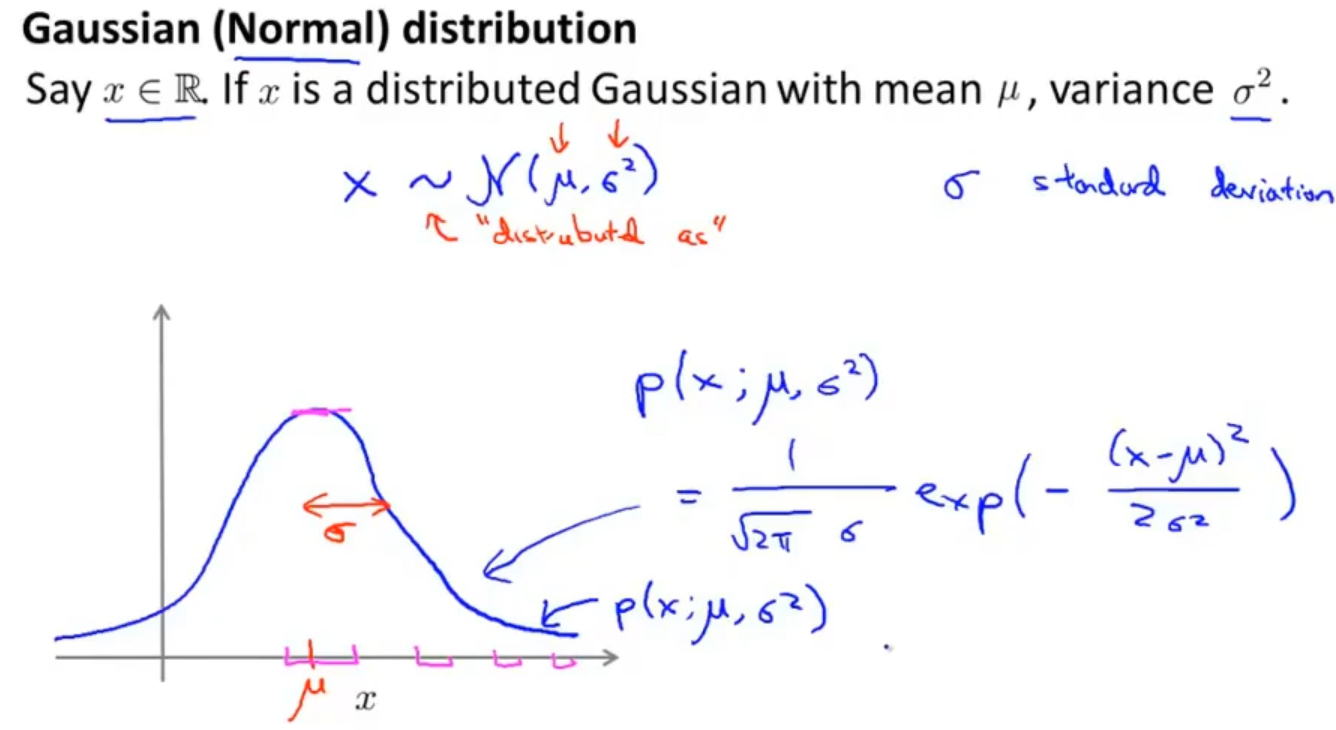
对于不同的 μ 和 σ ,高斯分布呈现出不同的图像
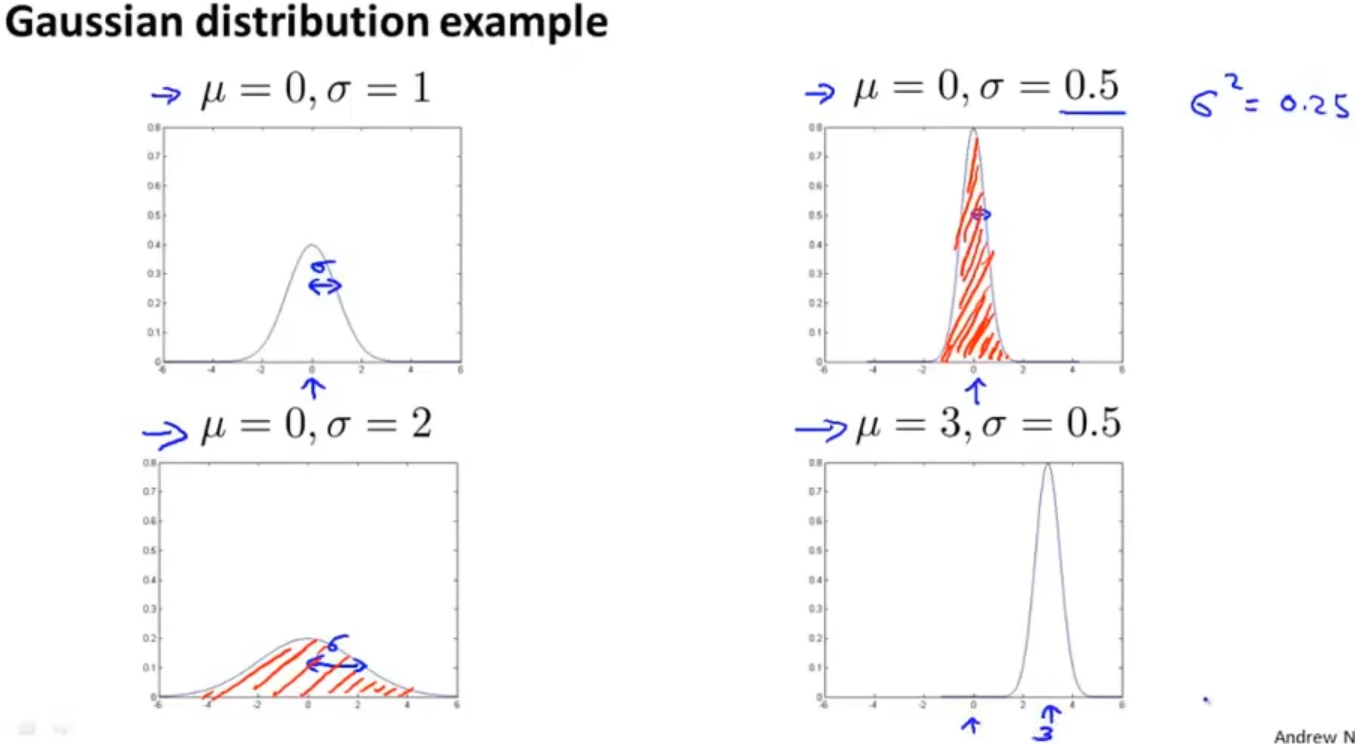
在高斯分布中需要记住的两个公式分别为: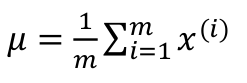 、
、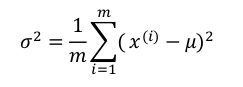
值得注意的是在机器学习中方差通常除以 m,而在统计学中是除以(m − 1)。这两个公式在理论和数学特性上稍有不同,但在实际使用中由于数据集比较大,所以几乎可以忽略不计
1.3 异常检测算法 Algorithm
介绍了异常检测和高斯分布之后,我们就可以把二者结合起来了
首先计算训练集中每一个特征的均值 μ 和方差 σ2 ,然后分别求得相应的概率密度函数 P(x;μ,σ2),最后把所有概率密度函数 P(x;μ,σ2) 进行连乘得到 P(x)
当出现一个新的实例时,可以将实例带入 P(x) 求解其值,将 P(x) 与 ε 比较来判断是否为异常值,其中 P(x) 公式定义为: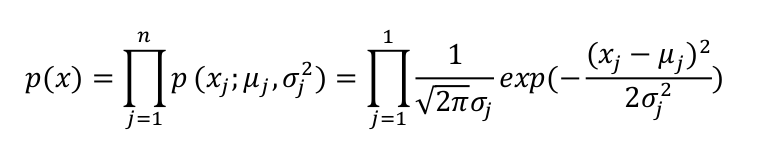

算法的详细过程如下:

举例说明:

1.4 开发和评估异常检测系统 Developing and evaluating an anomaly detection system
异常检测算法其实是属于无监督学习算法。但如果我们的数据是带标签的,我们可以把它先看成监督学习算法。具体步骤就是先进行数据划分,从正常数据种选择一部分作为训练集,然后用剩下的正常数据和异常数据分别构建交叉检验集和测试集

举个例子:比如有10000个正常的飞机引擎和20个有问题的飞机引擎,首先从10000个正常的飞机引擎选取6000个作为训练集,再组成拥有2000个正常的飞机引擎和10个有问题的飞机引擎的交叉验证集和测试集

用训练集训练出模型后就可以在交叉验证集和测试集上预测了,对于交叉验证集,可以尝试使用不同的 ε 值作为阈值,最后可以选出 ε ,然后对测试集进行预测,计算异常检验系统的F1值,或者查准率与查全率之比

1.5 异常检测与监督学习对比 Anomaly Detection vs. Supervised Learning
在提出将有标签的数据进行异常检测后,就会思考我们为什么不直接使用逻辑回归或者神经网络呢?
那我们就来看一看异常检测和有监督学习之间的对比
异常检测适用于少量正类(异常数据),大量负类,异常种类复杂,未知异常与已知异常不同的情况下,比如:诈骗检测、生产检测之类
监督学习适用于大量的正类、负类,未知异常与已知异常相似的情况下,比如:肿瘤分类、邮件过滤等

1.6 选择特征 Choosing what features to use
特征的选择对异常检测算法来说是十分关键的,如果特征不符合高斯分布,建议将数据转换成高斯分布,比如 :使用对数函数 x = log(x + c) (其中c为非负常数或者 x = xc ,c为 0-1 之间的一个分数)

在异常检测过程中,也可能遇到一些异常的数据是与正常数据难以分开的,可以使用误差分析帮我们分析是否存在问题,也可以增加一些新的特征,增加新特征后的新算法能够更好地进行异常检测
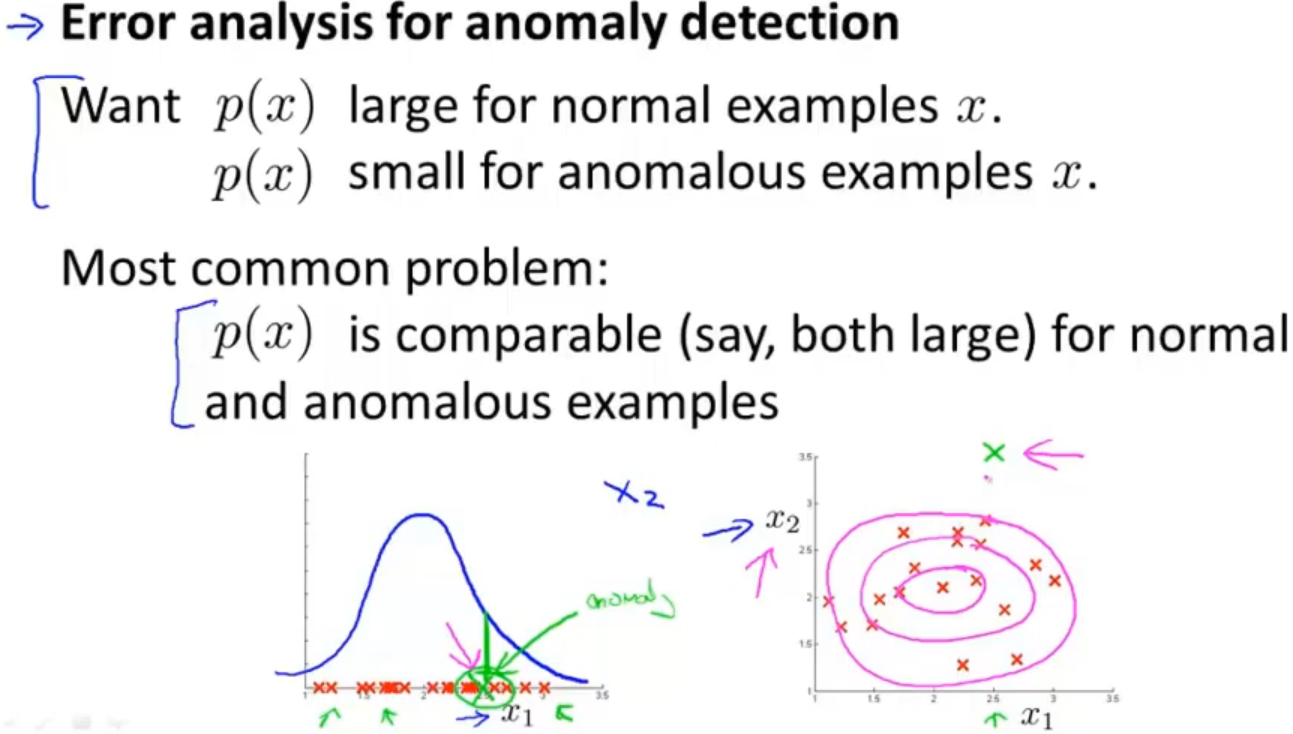
例如,在检测计算机状况的例子中,可以用 CPU负载与网络通信量的比例作为一个新的特征,如果该值异常地大,便有可能意味着该服务器是陷入了一些问题中

1.7 多变量高斯分布 Multivariate Gaussian distribution
假设有两个特征是相关的,对于一般的高斯分布是不太好识别异常数据的,原因在于,一般的高斯函数模型尝试同时抓住两个特征的偏差,就会得到如下图中的粉色判断边界,假如绿色叉是异常点,那就很难将它识别出来了
但是对于多元高斯分布来说,它得到就是蓝色判断边界,就可以很好的把绿色叉区分开来
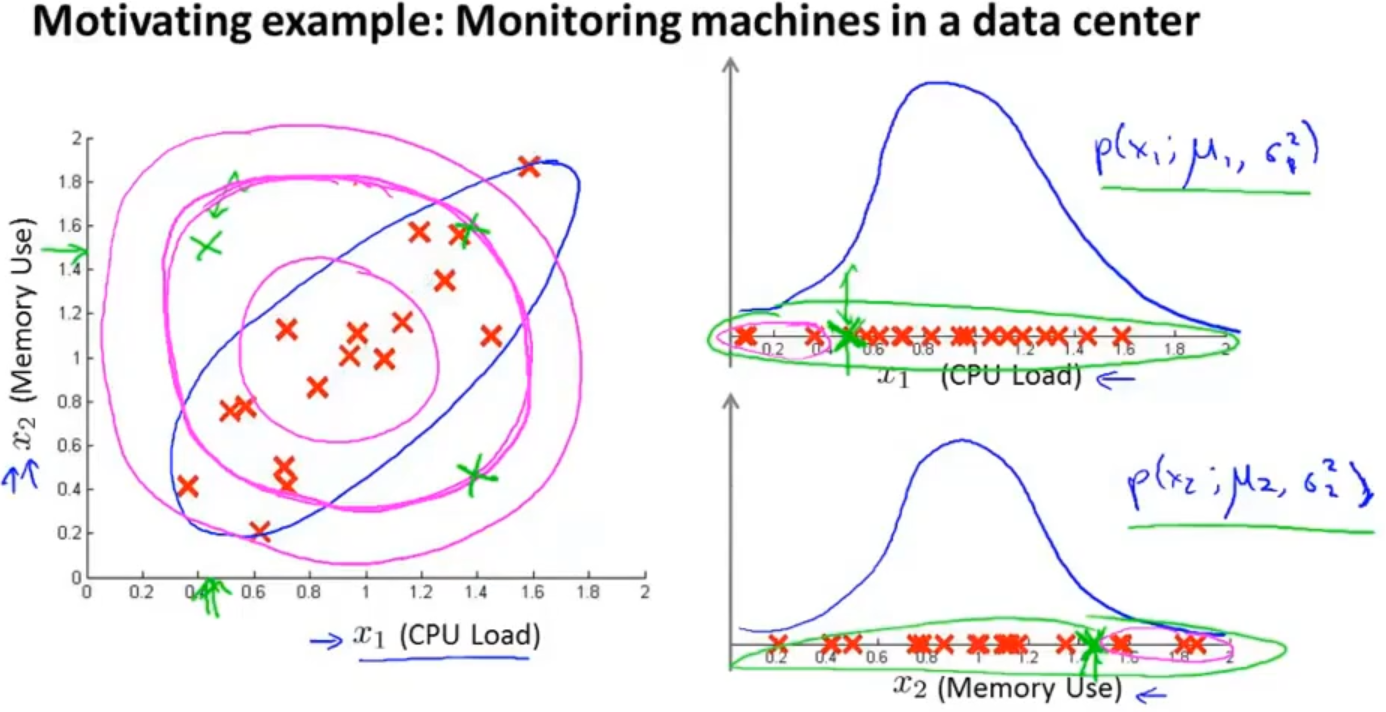
在高斯分布模型中是通过分别计算每个特征对应的几率,将其累乘起来,得到 p(x)
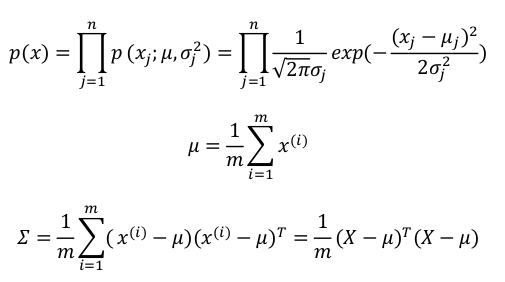
而多元高斯分布模型是通过构建特征的协方差矩阵,使用所有的特征一次性计算出 p(x)。计算步骤:先计算所有特征的平均值 μ,然后再计算协方差矩阵 Σ
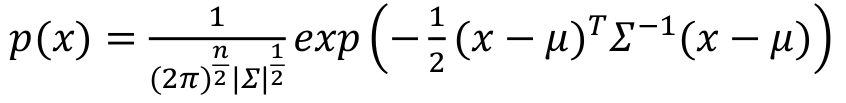
其中: μ 是一个向量,其每一个单元都是原特征矩阵中一行数据的均值,|Σ|是矩阵的行列式

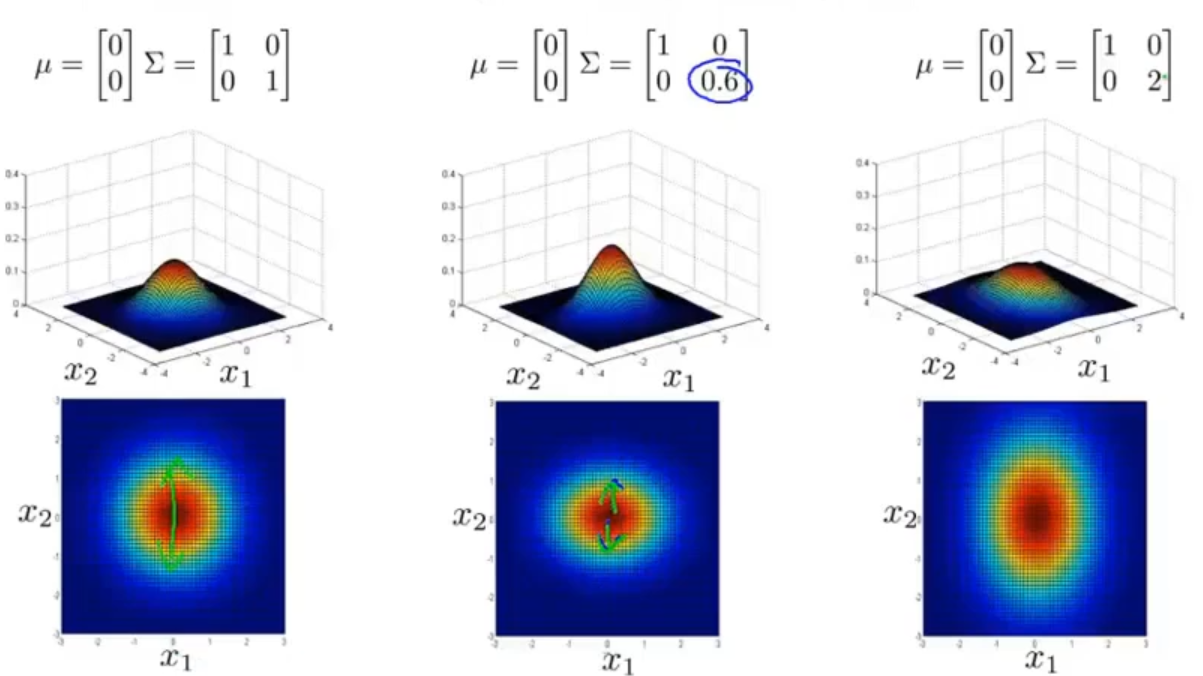
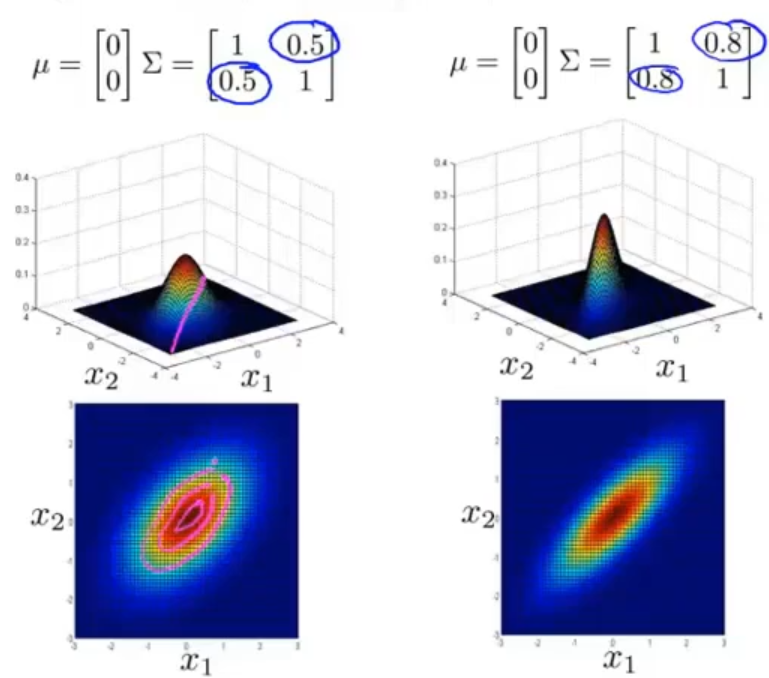
不同的均值 μ 和协方差矩阵 Σ 都会对模型产生影响
左1为正常图像,左2图像是 x2 特征的偏差较小,中间图像是 x2 特征的偏差较大,右2图像是不改变偏差,增加两者之间的正相关性,右1图像不改变偏差,增加两者之间的负相关性
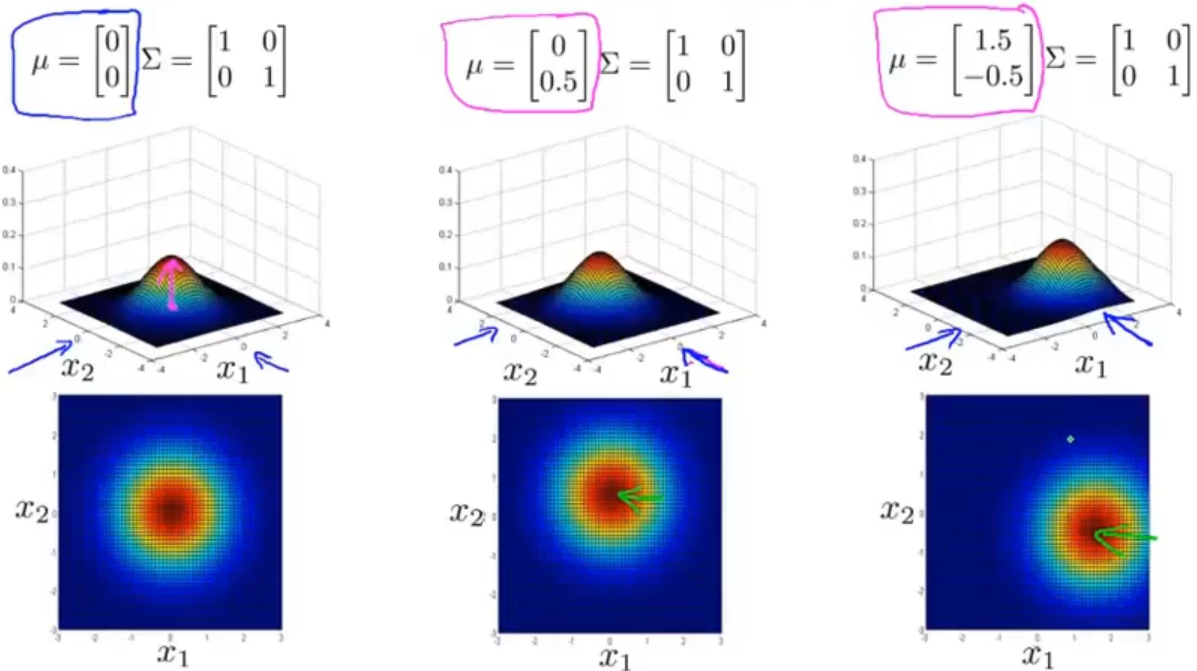
不同的均值 µ 对模型的影响
1.8 使用多元高斯分布进行异常检测 anomaly detection using the multivariate Gaussian distribution
使用元高斯分布进行异常检测的步骤:先计算出均值 µ 和协方差矩阵 Σ ,然后对新实例 x, 根据公式计算其 p(x) 的值,如果小于 ε 则异常

在一般的高斯分布模型和多元高斯分布模型的对比中,对于多元高斯分布模型,如果其协方差矩阵只有正对角线上元素非零,则退化为原始高斯分布模型

更具体的对比就是
一般的高斯分布模型:不能捕捉特征之间的相关性,但可以通过将特征进行组合的方式来解决;计算代价小,可以适用于大规模的特征
多元的高斯分布模型:自动捕捉特征之间的相关性;计算代价较大,适用于训练集较小的样本;训练的大小 m 必须要大于特征数量n,通常需要m ≥ 10n,否则会导致协方差矩阵不可逆

模型选择:
如果特征之间在某种程度上相互关联,可以通过构造新特征的方法来捕捉这些相关性,可以使用原高斯分布模型
如果训练集不是太大,并且没有太多的特征,可以使用多元高斯分布模型