[BZOJ1027][JSOI2007]合金(凸包+最短路)
题面
某公司加工一种由铁、铝、锡组成的合金。他们的工作很简单。首先进口一些铁铝锡合金原材料,不同种类的原材料中铁铝锡的比重不同。然后,将每种原材料取出一定量,经过融解、混合,得到新的合金。新的合金的铁铝锡比重为用户所需要的比重。
现在,用户给出了n种他们需要的合金,以及每种合金中铁铝锡的比重。公司希望能够订购最少种类的原材料,并且使用这些原材料可以加工出用户需要的所有种类的合金。
分析
容易发现(c=1-a-b),那么就没必要考虑(c),只考虑(a,b). 我们先考虑2种合金((a_i,b_i)(a_j,b_j))混合的情况,设比例分别为(lambda,mu(lambda+mu=1)),那得到的新合金就是((lambda a_i+mu a_j,lambda b_i+mu b_j)).把((a,b))看成平面直角坐标系上的一个点(A_i),设原点为(O).那么得到的新合金为(lambda vec{OA_i}+mu vec{OA_j}). 由于(lambda+mu=1)根据向量知识可以得到,新的合金在点(A_i,A_j)的连线上。
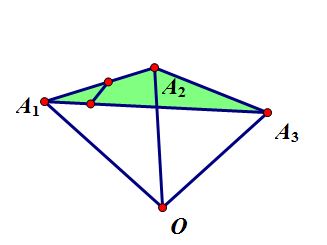
再考虑3种的情况.如上图,在两两相加形成的线段上任取两个点,新的合金在两点连线上。无数多的线段叠加在一起,就得到了一个三角形区域。以此类推,(n)种合金能够合成的金属对应的点在包含这(n)个点的多边形内
那么问题变成了,选择最少的点,使得这些点构成的凸包内部含有所有需要的点。我们可以枚举可能成为凸包的线段(A_iA_j),从(i)向(j)连一条边权为1的边。判断是否可能在凸包上,只需要用叉积判断是否存在点在向量(vec{A_iA_j})右侧即可,注意特判共线但不在线段上的情况。这一步的复杂度是(O(n^2m)).这样图上一个回路就对应一个凸包,Floyd求最小环即可。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define maxn 500
#define eps 1e-7
#define INF 0x3f3f3f3f
using namespace std;
typedef double db;
struct Vector{
db x;
db y;
Vector(){
}
Vector(db _x,db _y){
x=_x;
y=_y;
}
friend Vector operator + (Vector p,Vector q){
return Vector(p.x+q.x,p.y+q.y);
}
friend Vector operator - (Vector p,Vector q){
return Vector(p.x-q.x,p.y-q.y);
}
};
db cross(Vector p,Vector q){
return p.x*q.y-p.y*q.x;
}
db dot(Vector p,Vector q){
return p.x*q.x+p.y*q.y;
}
inline int sgn(double x){
if(fabs(x)<=eps) return 0;
else if(x>0) return 1;
else return -1;
}
int n,m;
Vector a[maxn+5],b[maxn+5];
int dist[maxn+5][maxn+5];
bool check(int p,int q){
for(int i=1;i<=m;i++){
int f=sgn(cross(a[q]-a[p],b[i]-a[p]));
if(f<0) return 0;//如果有点在PQ右侧,说明一定不是凸包的边
if(f==0&&sgn(dot(b[i]-a[p],b[i]-a[q]))>0) return 0;//如果共线但不在线段PQ上
}
return 1;
}
int floyd(){//找出包含所有b[i]的边数最少的凸包,因为有向图,直接输出dist[i][i]
int ans=INF;
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
}
}
for(int i=1;i<=n;i++) ans=min(ans,dist[i][i]);
return ans;
}
int main(){
db u,v,w;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%lf %lf %lf",&u,&v,&w);
a[i]=Vector(u,v);
}
for(int i=1;i<=m;i++){
scanf("%lf %lf %lf",&u,&v,&w);
b[i]=Vector(u,v);
}
memset(dist,0x3f,sizeof(dist));
for(int i=1;i<=n;i++){
// dist[i][i]=0;
for(int j=1;j<=n;j++){
//看看i->j这条边是否可能成为凸包的边
if(check(i,j)){
// printf("%d->%d
",i,j);
dist[i][j]=1;
}
}
}
// memcpy(dist,edge,sizeof(edge));
int ans=floyd();
if(ans>n) ans=-1;
printf("%d
",ans);
}