3张图带你看懂扩展KMP(EXKMP)
约定:
对于一个字符串(s),我们规定(s[l,r])表示字符(s[l],s[l+1],s[l+2],dots,s[r-1],s[r])按顺序拼接成的字符串.s的下标从1开始.(s[1,i] (i in[1,n]))表示(s)的一个前缀,(s[i,n](i in[1,n]))表示(s)的一个后缀
扩展KMP解决的问题
定义母串s和子串t,s的长度为n,t的长度为m.求字符串t与字符串s的每一个后缀 的最长公共前缀。扩展KMP算法可以求出一个extend数组,其中(extend[i])表示(t)与(s[i,n])的公共前缀长度。如s=“aaaabaa”,t="aaaaa",那么extend={4,3,2,1,0,2,1}
显然(forall j in [1,extend[i]],t[1,j]=s[i,i+j-1])
扩展KMP的过程
求extend
类似KMP算法中的next(fail)数组,我们定义(nex[i])表示(t)与(t[i,n])的公共前缀长度。假设我们已经求出了(t)的(nex),那么如何求(extend)呢?
扩展KMP和KMP一样是一个递推的过程。当前我们求出了([1,i-1])的(extend),我们现在要求(extend[i]).我们维护(r)表示(t)最远在(s)上匹配到了哪里,即(r=max_{j=1}^i (j+extend[j]-1)),并且记录(r)取最大值的位置(p_0).我们考虑(t)从(p_0)开始匹配的情况,容易发现(s[i])位置对应的是(t[i-p_0+1]).我们想从已知中推出(i)之后的匹配状态,注意到(nex[i-p_0+1])可以表示(i)往后的匹配长度,如下图所示(t[1,nex[i-p_0+1]]=t[i-p_0+1,i-p_0+nex[i-p_0+1]])
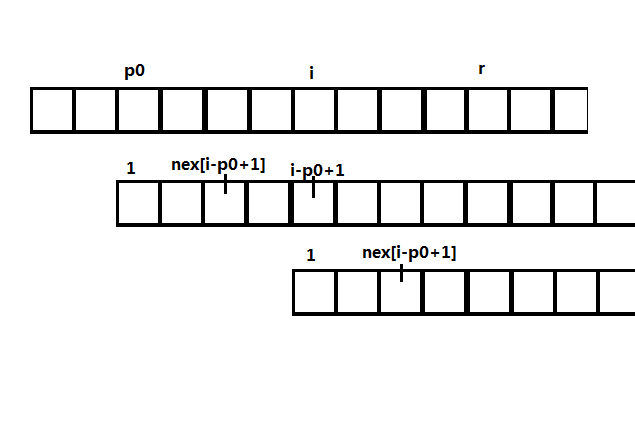
根据(nex[i-p_0+1])的大小,分两类讨论
(1) 当(i+nex[i-p_0+1]<r)
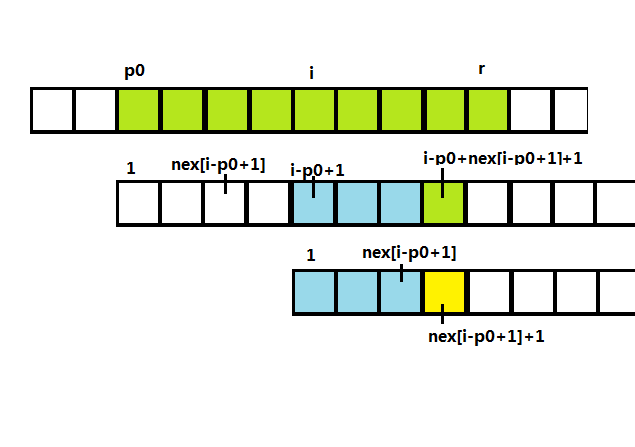
根据(nex)的定义,我们有(t[1,nex[i-p_0+1]]=t[i-p_0+1,i-p_0+nex[i-p_0+1]]),即图中两块蓝色部分相等。
又因为(t)在(p_0)时能与(s[p_0,n])匹配到(r)(绿色部分),所以(t[i-p_0+1,i-p_0+nex[i-p_0+1]]=s[i,i+nex[i-p_0+1]-1])(蓝色部分等于上方绿色部分)。
所以(t[1,nex[i-p_0+1]]=s[i,i+nex[i-p_0]-1]),也就是说,(extend[i])必然不小于(nex[i-p_0+1]).
考虑(t[nex[i-p_0+1]+1])(黄色部分),若(s[i+nex[i-p_0+1]]=t[nex[i-p_0+1]]),则由于t一直匹配到r,且(i+nex[i-p_0+1]<r) , (t[i-p_0+nex[i-p_0+1]+1]=t[nex[i-p_0+1]])。(黄色部分等于上面第1行绿色部分,上面第1行绿色部分又等于第2行绿色部分). 那么根据定义,nex可以再增加1,矛盾。因此(extend[i]=nex[i-p_0+1])
(2) 当(i+nex[i-p_0+1] geq r)
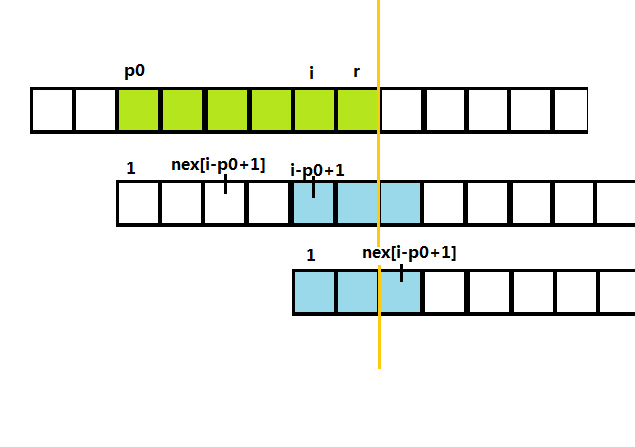
显然有(s[i,r]=t[i-p_0+1,r-p_0+1]),
根据nex的定义有(t[i-p_0+1,r]=t[1,r-(i-p_0+1)+1])
那么(s[i,r]=t[1,r]),也就是说,(extend[i])必然不小于(nex[i-p_0+1]).但是不像情况1,我们知道r后面的s与t的匹配情况。所以这里就从i开始向后暴力匹配。匹配完成后r必定会向右移动,更新p0,r.
void get_extend(char *s,int n,char *t,int m,int *extend){
static int nex[maxn+5];
get_nex(t,m,nex);
extend[1]=0;
while(s[extend[1]+1]==t[extend[1]+1]) extend[1]++;//暴力初始化extend[1]
for(int i=2,p0=1,r=p0+extend[p0]-1;i<=n;i++){
if(i+nex[i-p0+1]-1<r) extend[i]=nex[i-p0+1];//情况1
else{
//情况2
extend[i]=max(r-i+1,0);//extend[i]>=r-i+1
while(s[i+extend[i]]==t[1+extend[i]]) extend[i]++;
p0=i;
r=i+extend[i]-1;
}
}
}
求nex
类比KMP求nex数组是自己和自己匹配。EXKMP求nex也是t和t求一遍nex
void get_nex(char *t,int m,int *nex){
nex[1]=m;//nex[1]表示t和t匹配,显然为m
nex[2]=0;
while(t[2+nex[2]]==t[1+nex[2]]) nex[2]++;//暴力初始化nex[2]
for(int i=3,p0=2,r=p0+nex[p0]-1;i<=m;i++){
if(i+nex[i-p0+1]-1<r) nex[i]=nex[i-p0+1];//情况1
else{
nex[i]=max(r-i+1,0);//情况2
while(t[i+nex[i]]==t[1+nex[i]]) nex[i]++;//暴力匹配
p0=i;
r=i+nex[i]-1;
}
}
}
容易发现在i时需要的nex都是求过的,所以正确性不会有问题
扩展KMP的时间复杂度分析
求extend
对于情况(1),无需做任何匹配即可计算出extend[i],对于情况(2),每次从s中未被匹配的位置r开始匹配,匹配过的位置不再匹配,也就是说对于母串的每一个位置,都只匹配了一次,所以算法总体时间复杂度是(O(n))的
求nex
与求extend类似,是(O(m))的
综上,时间复杂度为(O(n+m))
代码LuoguP5410 [模板]扩展KMP
//https://www.luogu.com.cn/problem/P5410
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 100000
using namespace std;
int n,m;
char s[maxn+5],t[maxn+5];
void get_nex(char *t,int m,int *nex){
nex[1]=m;
nex[2]=0;
while(t[2+nex[2]]==t[1+nex[2]]) nex[2]++;
for(int i=3,p0=2,r=p0+nex[p0]-1;i<=m;i++){
if(i+nex[i-p0+1]-1<r) nex[i]=nex[i-p0+1];
else{
nex[i]=max(r-i+1,0);
while(t[i+nex[i]]==t[1+nex[i]]) nex[i]++;
p0=i;
r=i+nex[i]-1;
}
}
}
void get_extend(char *s,int n,char *t,int m,int *extend){
static int nex[maxn+5];
get_nex(t,m,nex);
for(int i=1;i<=m;i++) printf("%d ",nex[i]);
printf("
");
extend[1]=0;
while(s[extend[1]+1]==t[extend[1]+1]) extend[1]++;
for(int i=2,p0=1,r=p0+extend[p0]-1;i<=n;i++){
if(i+nex[i-p0+1]-1<r) extend[i]=nex[i-p0+1];
else{
extend[i]=max(r-i+1,0);
while(s[i+extend[i]]==t[1+extend[i]]) extend[i]++;
p0=i;
r=i+extend[i]-1;
}
}
}
int f[maxn+5];
int main(){
// freopen("input.txt","r",stdin);
scanf("%s",s+1);
scanf("%s",t+1);
n=strlen(s+1);
m=strlen(t+1);
get_extend(s,n,t,m,f);
for(int i=1;i<=n;i++) printf("%d ",f[i]);
}