题面
给出一棵n个点的树,要求把它画在圆上,且边不相交,画法与排列一一对应(即旋转后相同的算不同种),求方案数。如下图是4个点的树(T:V={1,2,3,4},E={(1,2),(1,3),(2,4)})的方案:
图片来自cf原题
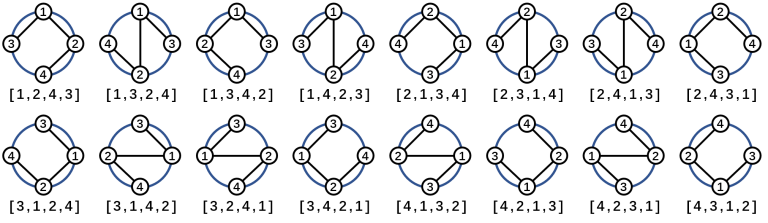
分析
对于x的子树,我们发现x的子树上的节点在圆上一定是一个连续区间,否则会出现下图的情况
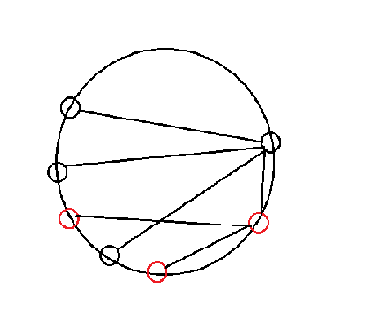
设deg[x]表示x的度数
对于非根节点x:
x有deg[x]-1个儿子,这些儿子排列的方案有((deg[x]-1)!)种,然后把根节点插到儿子与儿子相邻的任意一个位置,一共deg[x]个空,总答案为((deg[x]-1)! imes deg[x]=deg[x]!)
对于根节点x:
x本身的位置可以在圆上任选,有n种.x有deg[x]个儿子,排列方案为(n imes deg[x]!)
因此,总方案数为(n imesprod_{i=1}^n deg(i)!)
代码
#include<iostream>
#include<cstdio>
#define maxn 200005
#define mod 998244353
using namespace std;
int n;
long long fact[maxn];
int deg[maxn];
int main(){
int u,v;
scanf("%d",&n);
for(int i=1;i<n;i++){
scanf("%d %d",&u,&v);
deg[u]++;
deg[v]++;
}
fact[0]=1;
for(int i=1;i<=n;i++){
fact[i]=fact[i-1]*i%mod;
}
long long ans=1;
for(int i=1;i<=n;i++){
ans*=fact[deg[i]];
ans%=mod;
}
ans*=n;
ans%=mod;
printf("%I64d
",ans);
}