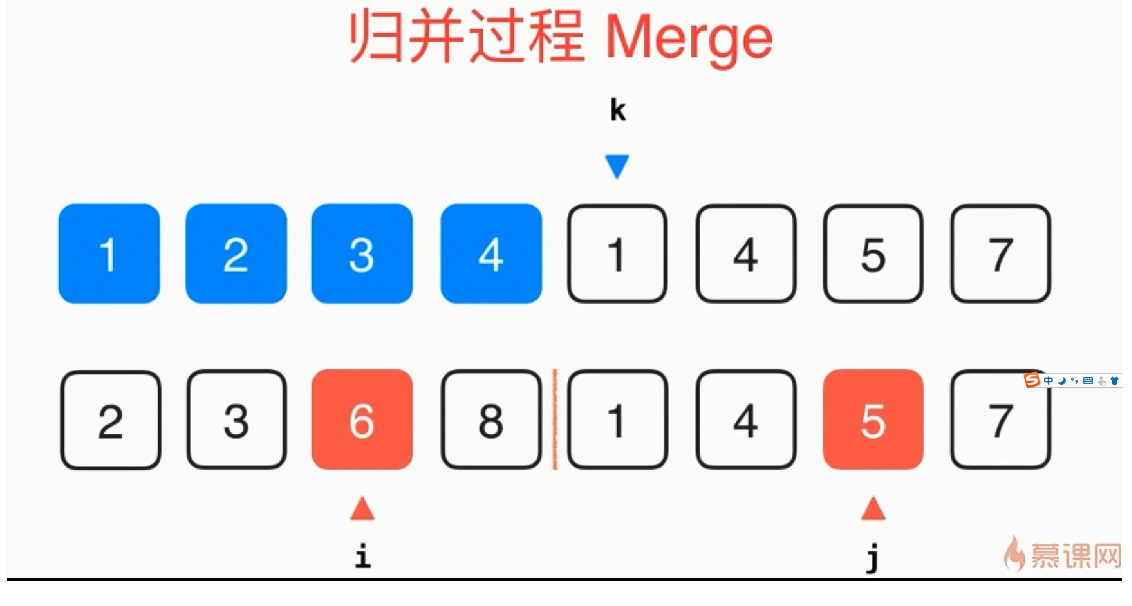
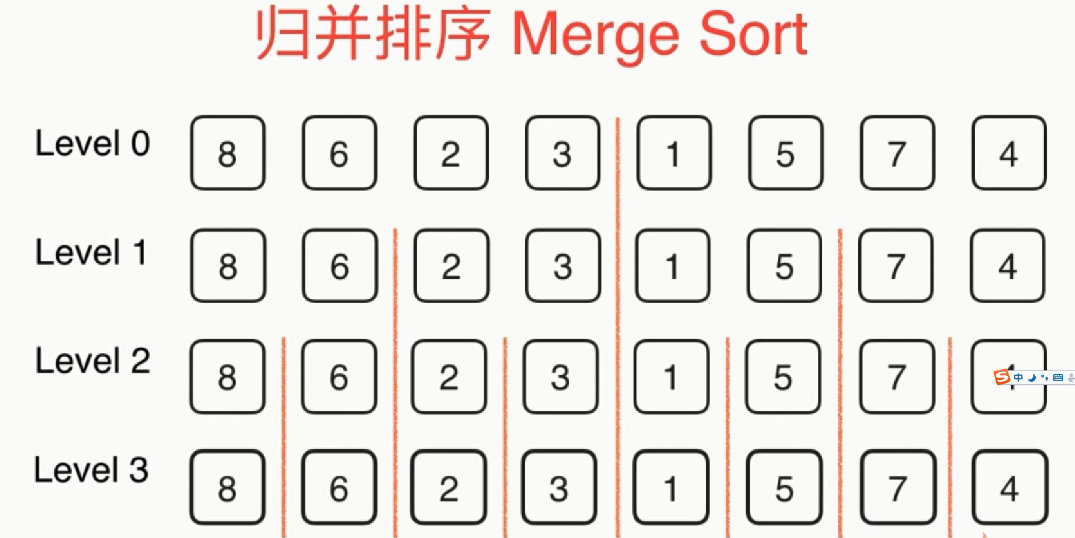
归并排序:将数组每次分成两部分分别排序,然后逐一合并
1 template<typename T> 2 void __merge(T arr[], int l, int mid, int r) { 3 int *aux = new int[r - l + 1];//开辟新的空间 4 for (int i = l; i <= r; i++) 5 aux[i - l] = arr[i]; 6 int i = l, j = mid + 1; 7 for (int k = l; k <= r; k++) { 8 if (i > mid) 9 { 10 arr[k] = aux[j - l]; 11 j++; 12 } 13 else if (j > r) { 14 arr[k] = aux[i - l]; 15 i++; 16 } 17 else if (aux[i - l] < aux[j - l]) 18 { 19 arr[k] = aux[i - l]; 20 i++; 21 } 22 else 23 { 24 arr[k] = aux[j - l]; 25 j++; 26 } 27 } 28 delete[] aux; 29 30 } 31 template<typename T> 32 void __mergeSort(T arr[], int l, int r) { 33 if (r - l <= 15) { 34 insertionSort(arr, l, r);//使用插入排序对其进行优化 35 return; 36 } 37 /*if(r-l<=15) { 38 insertionSort(arr,l,r); 39 return ; 40 } 41 */ 42 int mid = (l + r) / 2; 43 __mergeSort(arr, l, mid); 44 __mergeSort(arr, mid + 1, r); 45 if (arr[mid]>arr[mid + 1])//对近乎有序的数组的优化 46 __merge(arr, l, mid, r); 47 } 48 template<typename T> 49 void mergeSort(T arr[], int n) { 50 __mergeSort(arr, 0, n - 1); 51 } 52 template<typename T> 53 void mergeSortBU(T arr[], int n) {//自底向上排序 54 for (int sz = 1; sz <= n; sz += sz) 55 for (int i = 0; i + sz < n; i += sz + sz) 56 __merge(arr, i, i + sz - 1, min(n - 1, i + sz + sz - 1)); 57 }
快速排序:将数组分成两部分,使得组边部分小于标准,右边部分大于标准,这样就将标准元素放到了排序数组正确的位置

1 template<typename T>//找到一个索引使得arr[l...p-1]<v,arr[p+1..r]>v,这样v就在恰当的位置了 2 int __partition(T arr[], int l, int r) { 3 swap(arr[l], arr[rand() % (r - l + 1) + l]);//优化 4 5 T v = arr[l];//一个标准两个索引 6 int j = l;//使得arr[l+1...j] < v ; arr[j+1...i) > v,每次遇到小于v的元素进行交换, 扩充arr[l+1...j]的同时,将大于部分往后放 7 for (int i = l + 1; i <= r; i++) 8 { 9 if (arr[i] < v) { 10 j++; 11 swap(arr[i], arr[j]); 12 } 13 } 14 swap(arr[l], arr[j]);//将v放到恰当位置 15 return j; 16 } 17 template<typename T> 18 void __quickSort(T arr[], int l, int r) { 19 if (r - l <= 15) { 20 insertionSort(arr, l, r); 21 return; 22 } 23 int p = __partition(arr, l, r); 24 __quickSort(arr, l, p - 1); 25 __quickSort(arr, p + 1, r); 26 }
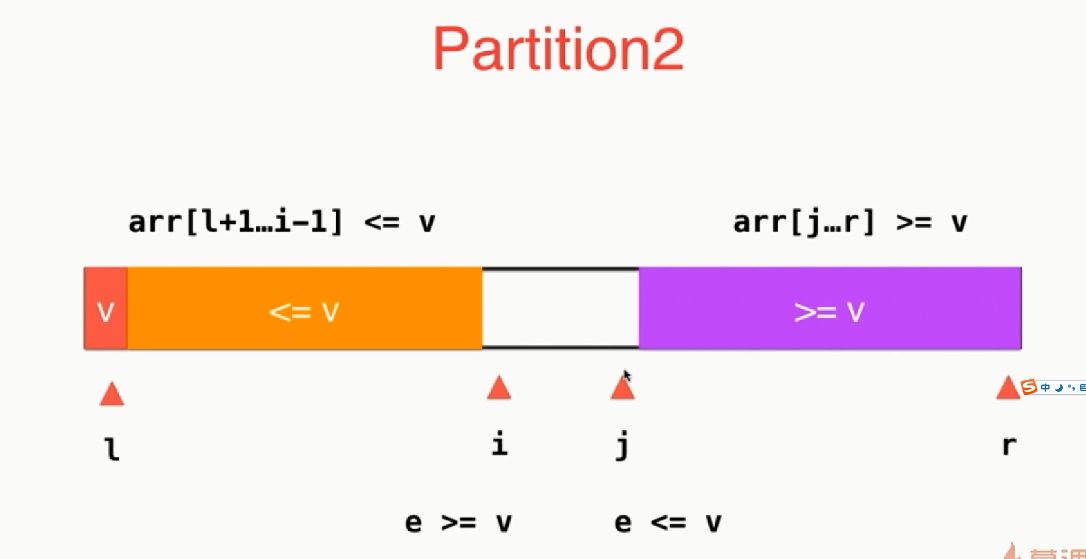
27 template<typename T>//找到一个索引使得arr[l...p-1]<v,arr[p+1..r]>v,这样v就在恰当的位置了 28 int __partition2(T arr[], int l, int r) { 29 swap(arr[l], arr[rand() % (r - l + 1) + l]);//优化,对于近乎有序的数组,快速排序会退化成一个O(n2)级别的算法 30 31 T v = arr[l];//一个标准两个索引 32 int i = l + 1, j = r; 33 while (true) { 34 while (i <= r && arr[i] < v) 35 i++; 36 37 while (j >= l + 1 && arr[j] > v) 38 j--; 39 if (i>j) break; 40 swap(arr[i], arr[j]); 41 i++; 42 j--; 43 } 44 swap(arr[j], arr[l]); 45 return j; 46 } 47 template<typename T> 48 void __quickSort2(T arr[], int l, int r) { 49 if (r - l <= 15) { 50 insertionSort(arr, l, r); 51 return; 52 } 53 int p = __partition2(arr, l, r); 54 __quickSort2(arr, l, p - 1); 55 __quickSort2(arr, p + 1, r); 56 } 57 template<typename T> 58 void quickSort(T arr[], int n) { 59 srand(time(NULL)); 60 __quickSort2(arr, 0, n - 1); 61 }
三路快排
1 //三路快速排序 2 template <typename T> 3 void __quickSort3Ways(T arr[], int l, int r) { 4 5 if (r - l <= 15) { 6 insertionSort(arr, l, r); 7 return; 8 } 9 10 swap(arr[l], arr[rand() % (r - l + 1) + l]); 11 12 T v = arr[l]; 13 14 int lt = l; // arr[l+1...lt] < v 15 int gt = r + 1; // arr[gt...r] > v 16 int i = l + 1; // arr[lt+1...i) == v 17 while (i < gt) { 18 if (arr[i] < v) { 19 swap(arr[i], arr[lt + 1]); 20 i++; 21 lt++; 22 } 23 else if (arr[i] > v) { 24 swap(arr[i], arr[gt - 1]); 25 gt--; 26 } 27 else { // arr[i] == v 28 i++; 29 } 30 } 31 32 swap(arr[l], arr[lt]); 33 34 __quickSort3Ways(arr, l, lt - 1); 35 __quickSort3Ways(arr, gt, r); 36 } 37 38 template <typename T> 39 void quickSort3Ways(T arr[], int n) { 40 41 srand(time(NULL)); 42 __quickSort3Ways(arr, 0, n - 1); 43 }