1.定义
哈夫曼树,是一类带权路径长度最短的树
2.名称
-
路径长度:指从树中一个结点到另一个结点之间的分支构成两个结点的路径,路径上的分支数目
-
带权路径长度:为从该结点到树根之间的路径长度与结点上权的乘积
-
带权路径长度之和:为树中所有叶子结点的带权路径长度之和,通常记作WPL。
若有n个权值为(w_1,w_2,...,w_n)的结点构成一棵有(n)个叶子结点的二叉树,则树的带权路径最小的二叉树叫做哈夫曼树。
3.例子
设:a为3,b为6,c为4,d为9
如下图就是一个哈夫曼树:
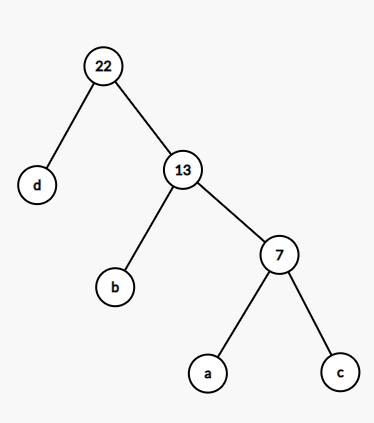
他的带权路径长度之和为:(9*1+6*2+4*3+3*3=42)