题目:
返回一个整数矩阵中最大子矩阵的和。
要求:
两人结对完成编程任务。
一人主要负责程序分析,代码编程。
一人负责代码复审和代码测试计划。
思想:
上一次的题目是返回一个整数数组中最大子数组的和;由于矩阵各个元素并不是完全可以
完全连续的,所以从二维下手没能打开思路想到更好的方法,不过,想到上次的一维求和方法
我可以将二维数组转变为多个一维数组求和,然后将所有数组求得的最大值再进行比较,得到
矩阵最大子矩阵的和,方法的好处是解决了各元素排列难以是矩阵的问题,同时又结合了之前
的方法,无需再想复杂的算法了。(临时想到的直接从二维开始计算的方法,难以形成程序,
并且验证很困难,选择暂时放弃)
程序源代码:
1 #include<iostream> 2 #include<ctime> 3 using namespace std; 4 int demo(int a[],int n){ //求一维数组最大数组元素之和 5 int result=a[0],sum=0,k=0; 6 for ( int j=0; j<n; j++ ) { 7 if ( sum>=0 ){ sum+=a[j]; } 8 else { sum=a[j]; } 9 if( result < sum ) { 10 result=sum; 11 } 12 } 13 return result; //返回最大值 14 } 15 int main() 16 { 17 srand((unsigned)time(NULL)); 18 int m,n; //矩阵行m与列n 19 cout<<"求矩阵中子矩阵元素和最大的值!"<<endl; 20 cout<<"请输入行数m:"; 21 cin>>m; 22 cout<<"请输入列数n:"; 23 cin>>n; 24 int * temp=new int[n]; //临时数组,最终求得结果作为元素暂存 25 int * compare=new int[(1+m)*m/2]; //比较所有暂存元素的最大值 26 int ** arr=new int*[n]; //矩阵,二维数组 27 int g=0,randoms; //g用于累加计数 28 for ( int i=0; i<m; i++ ) { //随机产生矩阵列表 29 temp[i]=0; 30 arr[i]=new int[n]; 31 for(int j=0; j<n; j++){ 32 randoms = ( -rand()%100 + ( rand()%100 ) ); 33 arr[i][j] = randoms; 34 cout<<arr[i][j]<<" "; 35 } 36 cout<<endl; 37 } 38 for(int k=1;k<=m;k++){// 表示k行数组各列元素的和 39 for(int s=0;s<m+1-k;s++){ 40 for(int t=0;t<n;t++){ 41 for(int h=0;h<k;h++){ 42 temp[t]+=arr[s+h][t]; 43 } 44 } 45 compare[g]=demo(temp,n); //调用demo 46 g++; 47 for(int l=0;l<n;l++){ 48 temp[l]=0; 49 } 50 } 51 } 52 for(int d=0;d<((1+m)*m/2);d++) //排序,求最大矩阵元素之和 53 { 54 int x; 55 56 for(int f=0;f<((1+m)*m/2)-d;f++){ 57 if(compare[f]<=compare[f+1]){ 58 x=compare[f]; 59 compare[f]=compare[f+1]; 60 compare[f+1]=x; 61 } 62 } 63 } 64 cout<<endl<<"子矩阵元素和最大的值="<<compare[0]<<endl; 65 return 0; 66 }
程序截图:
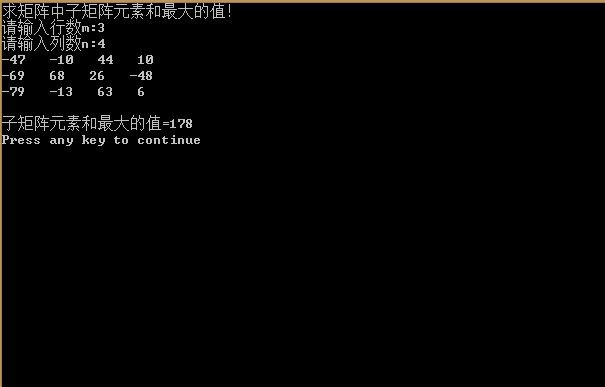
结对编程总结:
我的想法就是上面形成的程序,搭档的想法是将所有的矩阵一一计数,然后进行总体的比较,
关键是统计所有的矩阵方面,需要一定得次序,他的想法是:如选择a[3][2]这一点后,只从下标
均大于等于a[1][2]下标开始选择另一点,可以选择a[3][2]而不能选择a[1][1];依次从最开始的
地方计算,这样可以保证不会漏记不会多记,不过我认为工作量比较大,没有考虑实现,但是一
种很好的计数方法,比较有用。这种方法就由他来实现吧。通过这次编程实践,我觉得交流可以
扩充思路,互相指点,很有帮助。^_^