从傅里叶级数到傅里叶变换

周期信号的傅里叶级数和傅里叶系数如下所示

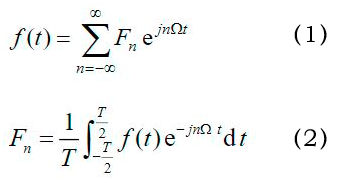
对于非周期信号，我们也想得到其频谱，为了得到非周期信号的频谱，可以将非周期信号可以看作周期无穷大的信号。下图展示了当一个周期信号的周期不断增大时，频谱的变化规律。

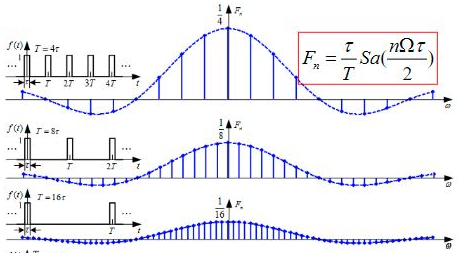
可以看到，当周期 (T) 增大，谱线高度将减小（这是由于随着周期增大，信号在时域上变得稀疏，信号的平均功率将减小），取极限后得到的每条谱线的高度都是0。为了解决这个问题，我们将(2)式两端乘以 (T)。我们知道，在离散频谱中，相邻两条谱线的间隔是 (Omega)，而 (T=frac{2pi}{Omega})，所以将(2)式两端乘以 (T) 就是将谱线除以它所占据的频带宽度再乘以(2pi)，因此得到的是频谱密度，如下图所示。

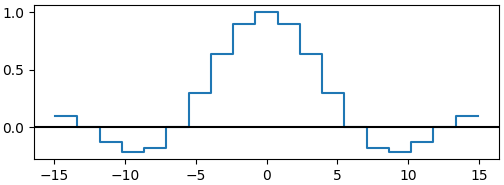
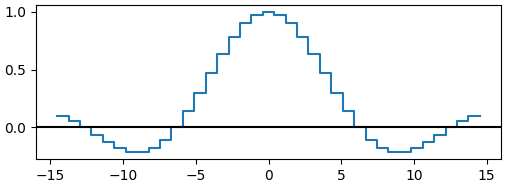
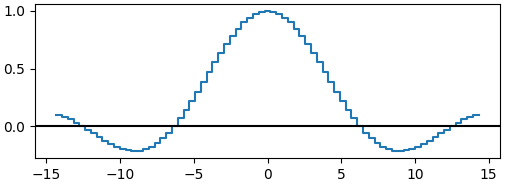
可以看到，随着周期增大，密度曲线逐渐趋于光滑，但是曲线的高度不会发生改变。当周期趋于无穷大时，密度曲线变成了完全光滑的曲线。

由于当周期趋于无穷大时，谱线间隔 (Omega) 趋于无穷小，因此谐波频率 (nOmega) 可以取到实数中的任意频率，用 (omega) 代替(2)式中的 (nOmega)，于是我们得到了非周期信号的傅里叶变换。

根据(1)式可以推导出非周期信号的傅里叶反变换

傅里叶反变换的式子也映证了“傅里叶变换得到的是频谱密度”这一物理含义

附: 频谱密度作图代码

import numpy as np
import matplotlib.pyplot as plt

tao = 1
T = 4*tao  # 通过这一行修改周期大小
Omega = 2*np.pi/T
n_max = int(14/(Omega*tao))+1

def Sa(w):
    if w == 0:
        sa = 1
    else:
        sa = np.sin(w)/w
    return sa

def F(n):
    return (tao/T)*Sa((n*Omega*tao)/2)

omega = []
dense = []
for n in range(-1*n_max,n_max+1):
    omega.append(n*Omega-Omega/2)
    omega.append(n*Omega)
    omega.append(n*Omega+Omega/2)
    dense.append(F(n)*2*np.pi/Omega)
    dense.append(F(n)*2*np.pi/Omega)
    dense.append(F(n)*2*np.pi/Omega)
plt.figure(figsize=(6,2))
plt.plot(omega,dense)
plt.axhline(y=0,color='black')
plt.show()