一、Array
1、创建语法
| 语言 | 语法 |
|---|---|
| Java C++ | int a[100] |
| Python | list=[] |
| JavaScript | let s = [1,2,3] |
2、数据结构
每当我们去申请创建一个数组时,计算机会在内存上开辟一段连续的地址,每一个地址都可以通过内存管理器直接进行访问。

3、时间复杂度
| 操作 | 时间复杂度 |
|---|---|
| prepend | O(1) |
| append | O(1) |
| lookup | O(1) |
| insert | O(n) |
| delete | O(n) |
优点:支持随机访问且访问每一个元素的时间复杂度相同都为 O(1)
缺点:插入一个元素时需要移动其他元素来为其腾出位置;同理可得,删除操作也需要挪动补齐;
如果插入到数组尾部的时候复杂度为 O(1),当然插入到头部时就需要移动整个数组,综合来说其操作复杂度都为 O(n),所以对于频繁插入、删除来说数组并不高效。


4、源码实现
二、Linked List
1、数据结构
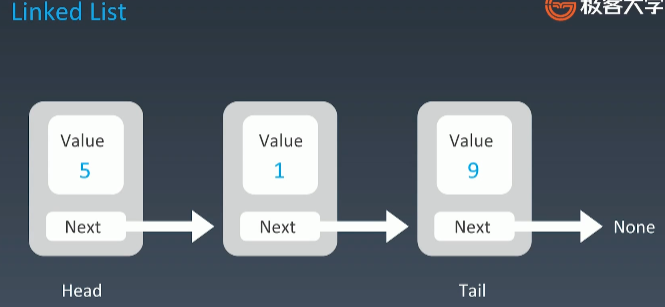
Java中LinkedList的结构部分的实现源码
/**
* Class to represent an entry in the list. Holds a single element.
*/
private static final class Entry<T>{
/** The element in the list. */
T data;
/** The next list entry, null if this is last. */
Entry<T> next;
/** The previous list entry, null if this is first. */
Entry<T> previous;
/**
* Construct an entry.
* @param data the list element
*/
Entry(T data){
this.data = data;
}
} // class Entry
2、时间复杂度
| 操作 | 时间复杂度 |
|---|---|
| prepend | O(1) |
| append | O(1) |
| lookup | O(n) |
| insert | O(1) |
| delete | O(1) |
增加结点

删除结点

优点:我们看到在增删结点时我们并没有像数组一样引起群移操作,正是因为这样所以链表的增加、移动、修改的效率是极高的,时间复杂度为 O(1)
缺点:也正是因为链表的数据结构,我们在访问链表中任意一个结点都需要从头结点或者尾节点(双向链表)一步一步向后(向前)挪动查找需要的结点,访问头结点尾节点时间复杂度为 O(1),其他结点综合来说为 O(n)
3、源码实现
三、Skip List (跳表)
跳表平时接触较少,在工程中主要让大家熟知的是 Redis 里面进行了运用,跳表的出现是为了解决 Linked List 随机访问(lookup)的效率。
1、给链表增加索引
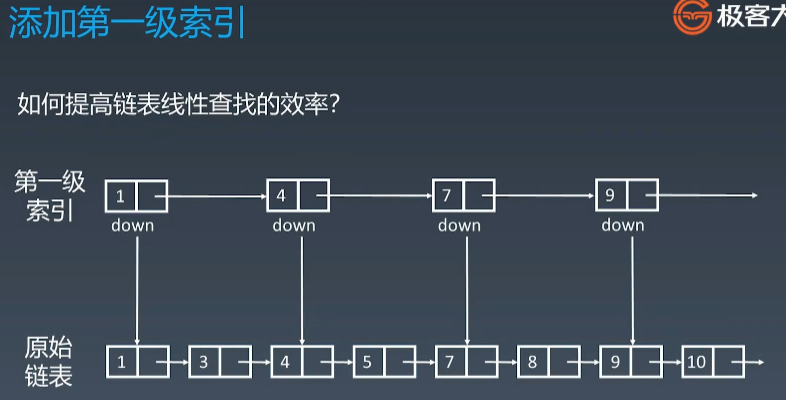
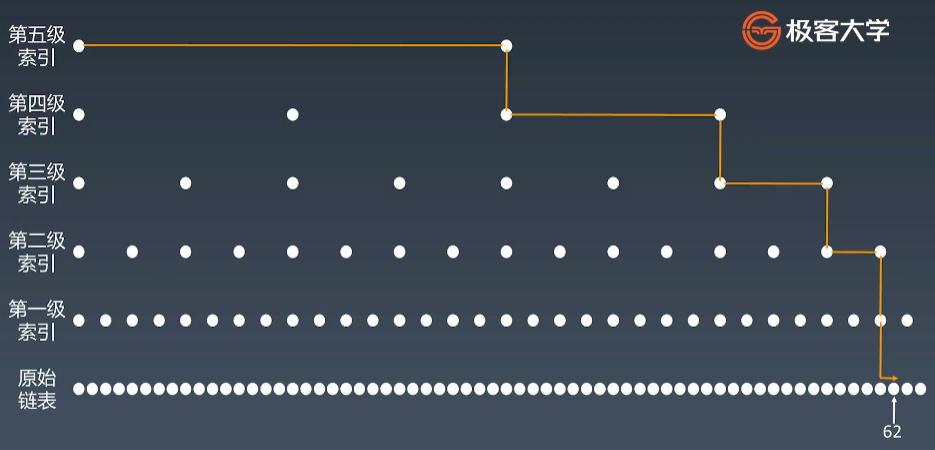
跳表通过应用升维以空间换时间的思想来优化链表的查找速度
2、时间复杂度
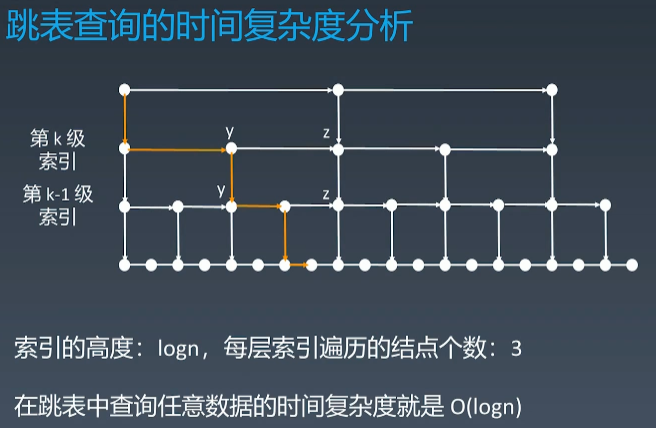
四、总结
- 没有完美的数据结构
- 数组的优势是随机访问效率高,但因其增删效率较低;
- 链表的出现来弥补数组的缺点,链表虽然增删效率高,但其不支持随机访问(只能通过遍历的方式访问结点);
- 正是因为如此才会有跳表的出现,通过空间换时间的思想增加索引来提高链表的访问效率,但其空间复杂度提高,若增删频繁维护成本较高;
- 数据结构里没有银弹,应该根据业务场景来寻找最优的数据结构
参考:极客大学-算法训练营-数组、链表、跳表 课程