寻找“最好”（1）——函数的极值

　　函数在其定 义域的某些局部区域所达到的相对 最大值或相对最小值。当函数在其 定义域的某一点的值大于该点周围 任何点的值时，称函数在该点有极 大值; 当函数在其定义域的某一点的值小于该点周围任何点的值时， 称函数在该点有极小值。这里的极 大和极小只具有局部意义。因为函 数的一个极值只是它在某一点附近 的小范围内的极大值或极小值。函 数在其整个定义域内可能有许多极 大值或极小值，而且某个极大值不 一定大于某个极小值。

单变量函数

极值点

　　单变量函数的最值问题较为简单，如果一有个函数f(x)，那么它的最值可能是函数的边界点或驻点。

　　假设f(x) = 2x² + x，求f(x)的最小值。

 

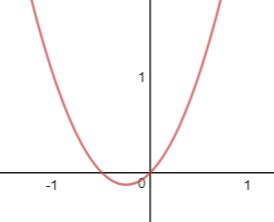
　　这个函数中x∈(-∞,+∞)，由图像可知，f(x)没有边界点，所以其驻点就是最小值。驻点是导数为0的点，在该点处，函数的变化率为0：

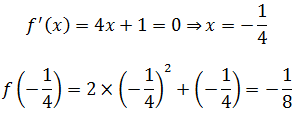
　　当x=-1/4时，f(x)有最小值-1/8。

极大还是极小

　　当然，极值是个局部概念，是相对于临近点的最小点，是否是最值就不一定了：

　　上图中ABCDEF几个点的导数都是0，它们的导数都是0，都是极值点，但只有B是最小点，最大点在无穷远端。现在问题来了，上图中B和C都是极值点，如果不作图的话，怎样判断最小值和最大值呢？

　　假设我们取到了一个极值点f(x₀)，对于x₀的临近点x₀ + β来说，f(x₀ + β)在x0出的泰勒展开(关于泰勒公式可参考《单变量微积分笔记31——幂级数和泰勒级数》)：

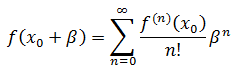
　　由于越展开，项的值越小，所以可以仅展开到二阶导数：

 

　　我们已经假定f(x₀)是极值点（f’(x₀) = 0），所以上式可以进一步化简为：

 

　　如果f(x₀)是极小值点，那么必然有f(x₀ + β) > f(x₀)，由于β²/2! > 0，所以f’’(x₀) > 0；反之，如果f(x₀)是极大值点，那么f’’(x₀) < 0；如果f’’(x₀) = 0，则有可能是一个拐点（多变量中也叫鞍点）。更多关于单变量函数的极值问题，可参考：《单变量微积分笔记7——曲线构图》《单变量微积分笔记8——最值问题和相关变率》

多变量函数的极值

极值点

　　与单变量函数类似，极值点只能在函数不可导的点或导数为零的点上取得。

 

　　对于一个多元函数f，如果有一个点满足f所有自变量的偏导都同时为0，那么这个点被称为f的临界点，也称为驻点。

　　对于二元函数f(x, y)来说，临界点(x₀, y₀)满足：

 

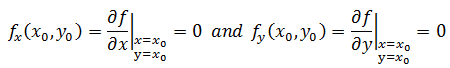
　　需要注意的是，导数为0的点仅仅是潜在的极值点，它也可能是鞍点，此时不是极大值也不是极小值：

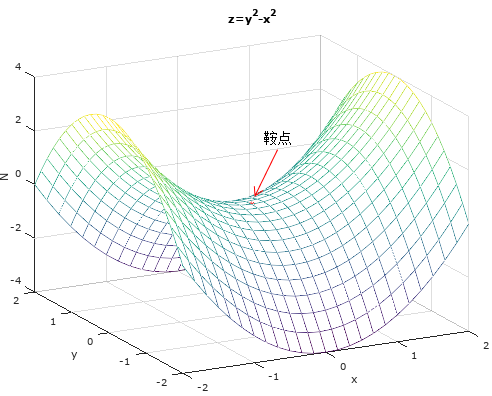
极大还是极小

　　通常使用二阶导数判断多变量函数的极值。f(x, y)的一个临界点是(x₀, y₀)，即f_x(x₀, y₀) = 0 && f_y(x₀, y₀) = 0，f的二阶导数是f_xx,f_xy,f_yy现在：

 

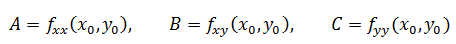
　　该临界点有如下结论：

　　更多关于多变量函数的极值问题，可参考：《多变量微积分笔记3——二元函数的极值》

 

海森矩阵

　　想要判断临界点是极大值还是极小值，最直观的方式当然是作图，但是二元函数通常很难作图，更多元的函数甚至无法作图，这就需要使用更高级的方法，这将涉及到海森矩阵（Hessian Matrix）。

 海森矩阵是啥？

　　泰勒公式也可以推广到多元函数，二元函数f(x,y)也可以在点(x₀, y₀)处开展开，展开形式与一元函数类似，只不过导数变成了偏导，所以泰勒的一阶展开式是：

　　f(x, y)的高阶导数可以分为4个子式，以二阶导数为例，f(x, y)的二阶导数共有包括混合偏导在内的2²个函数：

 

　　由此得到了泰勒的二阶展开式：

　　需要注意的是，混合偏导的系数也是混合的：(x–  x₀)(y –  y₀)。类似地，n阶偏导有2ⁿ个函数，其系数也相应的变化，在大多数时候只需要二阶展开。泰勒展开也可以推广到更多元函数，f(x₁,x₂,…x_n)在(x₁⁽⁰⁾,x₂⁽⁰⁾,…x_n⁽⁰⁾)处的二阶泰勒展开是：

　　我们希望把这个过于繁琐的展开式改写成较为简单的矩阵形式：

　　现在用矩阵代替原式：

　　把中间那个n阶方阵用H代替：

　　最终，多元函数的二阶泰勒展开式可以写成：

　　H(x₀)就是传说中的Hessian Matrix，被翻译成海森矩阵或黑塞矩阵，它是一个二阶导方阵。更多的时候，我们看到的是用莱布尼茨的方法表达海森矩阵：

判断极值

　　假设x₀是多元函数f的临界点，泰勒公式在x₀处展开。由于临界点的一阶导数为0，所以f(x)的展开式是：

 

　　现在，极值的判定法和单变量函数一致了：

　　 如果X^THX大于0，意味着f(x₀) < f(x)，即临界点小于附近的点，此时临界点是极小值；如果X^THX小于0，意味着f(x₀) > f(x)，即临界点大于附近的点，此时临界点是极大值；如果X^THX等于0，意味着f(x₀) = f(x)，临界点既不是极大值也不是极小值。

 

---

　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”