引例
天上掉钱了!都是红色的毛爷爷!同学们拿着盆跑到操场上接钱,当然谁的盆大谁接到钱的可能性就越大。
钱落下的位置是操场上的随机位置(每个位置等可能),接到钱的概率只与盆的大小相关(与几何度量相关),与盆的形状无关,每个同学接到钱的概率是 Area(盆)/Area(操场)。这是一个几何概型。
定义与公式
几何概型是一种概率模型,在这个模型下,E的样本空间是一个可度量的几何区域(操场),且每个样本点的发生具有等可能性(每个位置接到钱的几率相当)。这里的等可能性与上一章中提到的一样,客观上当你无法确定哪个事件更易发生的时候,只好认为是等可能。
古典概型与几何概型的主要区别在于试验的结果是无限个。骰子只有6个面,所以骰子的点数是有限个;骰子的落点可以是房间地面的任意位置,所以落点有无限个。
关于几何概型的定义,还有一种教科书的说法,大概是:样本点落入样本空间Ω中的某一可度量区域A的可能性大小与A的几何度量成正比,而与A的位置,形状无关。由此得到公式:

教科书的上的概念通常很严谨,但不易理解,置于是否能记住,随便吧,知道几何概型就是天上掉钱就好。
典型问题
很多问题可以转换为几何度量,例如一个人到单位的时间可能是8:00~9:00之间的任意一个时刻(将时间转换为一维线段);往一个方格中投一个石子,石子落在方格中任何一点上(将方格转换为二维坐标)。
示例1
甲乙二人在上午9:00 ~ 10:00间分别从AB两地出发,两人时速相等,都能够在10分钟内走完全程,那么二人相遇的几率是多少?
这是典型的几何概率,9:00 ~ 10:00间有无限多个时间,二人出发的时间点具有等可能性。以分钟为单位,把A出发的时间转换为线段:

把B出发的时间也加进来,形成二维坐标:

正方形就是样本空间Ω,其中的每一个点都代表AB出发的时间,也就是一个样本点,样本点有无数个。
A和B都是10分钟内走完全程,假设A先出发,想要相遇,B出发的时间一定在A出发后的10分钟内,设出发时间为T,则TB – TA < 10。由于B可能在A之前出发,所以加绝对值|TB – TA| < 10。将其转换为几何度量,符合条件的点全部落在绿色区域内:
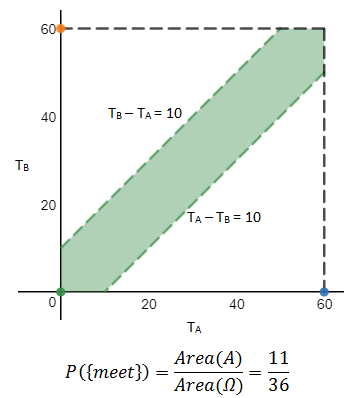
示例2
示例1还有另一个马甲,一对年轻人约定9:00 ~ 10:00在某地相亲见面,如果其中一方空等10分钟就会离开,他们成功见面的几率是多少?
对比示例1:

求解过程和结果完全一致。此类问题还有轮船相遇、汽车相遇等等。
示例3
A、B两盏路灯之间间隔30米,有关部门想在A、B间新添两盏相同的路灯C和D,A、C与B、D间隔都不小于10米的概率是多少?
A、B间的任意位置都可以放置路灯,设AC=x,BD=y。放置C时与D无关,此时需要满足10≤x≤30且0≤y≤0;同理,放置D时需要满足10≤y≤30且0≤x≤30。由此可以得到下图的几何图形:
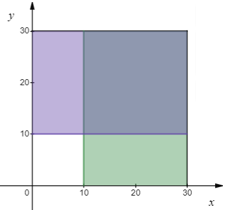
大正方形的面积是900,代表样本空间的度量,阴影部分的小正方向面积是400,代表所有符合条件的样本,因此最后的答案是4/9。
如果最后的位置必须是A、C、D、B,那么D的摆放就不是独立事件,它必须在C之后,摆放的空间依赖于C。仍然设AC=x,BD=y,需要满足x≥10,y≥10, 0<x+y<30。对于问题的解空间来说,x,y满足 0<x, 0<y, x+y<30。如此一来可以得到下面的几何图形:

0<x, 0<y, x+y<30是大三角形,x≥10,y≥10, 0<x+y<30 是小三角形,二者面积的比值就是问题的答案,结果是1/9。
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”
