多变量微积分笔记15——梯度场和势函数

梯度场的判别

　　如果一个向量场F = Mi + Nj是一个梯度场，它的势函数是f(x,y)，则：

  

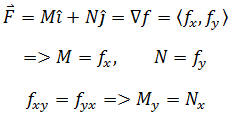
　　所以说，对于一个在平面内处处有定义且处处可导的向量场F = Mi + Nj，如果存在M_y = N_x，那么这个向量场是梯度场。

示例1

　　对于F = -yi + xj，用上面的判别法验证：

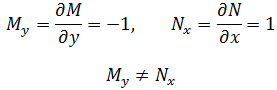
　　所以F = -yi + xj不是梯度场。

示例2

　　F = (4x² + axy)i + (3y² + 4x²)j，a是一个常数，当a 的值是多少时，F是梯度场？

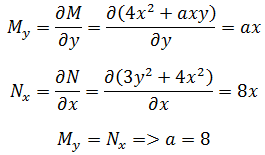
找出势函数

　　在上面的示例中，F = (4x² + 8xy)i + (3y² + 4x²)j是梯度场，那么如何找出它的势函数？在简单的梯度场中可以使用猜测法，但这并不总是管用，必须寻找到系统性的解决方案。

线积分法

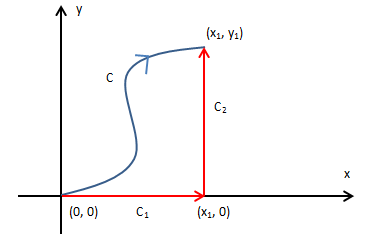
　　在梯度场中线积分的轨迹C从原点开始，终点是(x₁, y₁)：

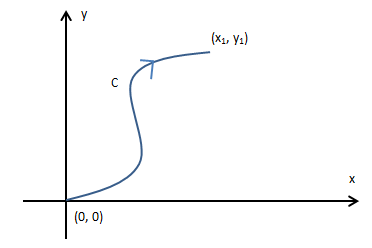
　　根据独立路径的原理，梯度场中的线积分只和起点终点有关，和路径无关，所以可以寻求更简单的计算方法：

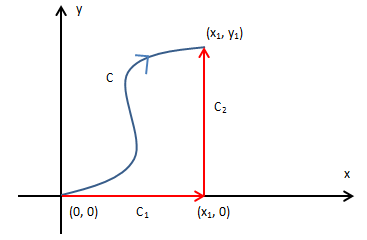
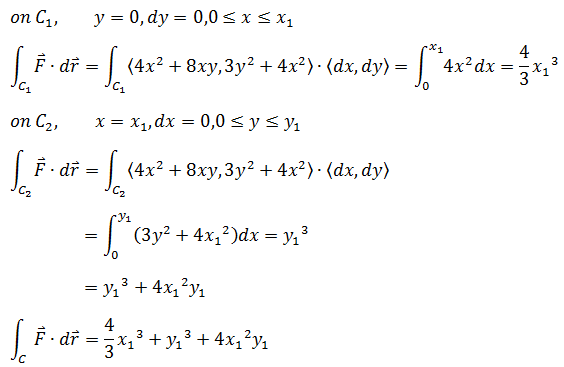
　　根据线积分基本定理：

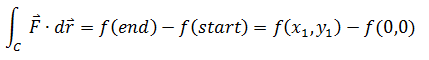
　　f(0,0)是一个常数，所以：

　　现在：

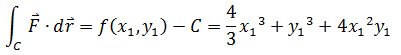
　　将x和y的下标去掉，就得到势函数：

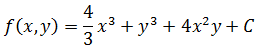
　　这里C是一个常数，说明f是一个势函数族，就像不定积分要加上常数C一样。

　　验证：

不定积分法

　　梯度场中的势函数 f 满足：

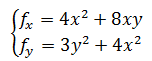
　　根据微积分基本定理，导数的积分等于原函数，这里将y看作常数，对f_x求x的积分：

 

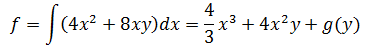
　　由于f_x是偏导，所以积分最后并不是加上常数C，而是一个关于y的函数g(y)。

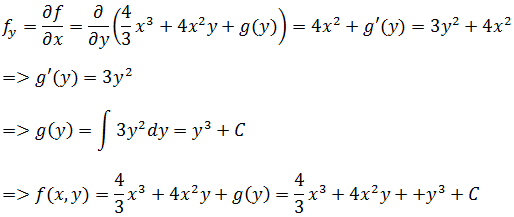
　　需要注意的是，g(y)中一定不会含有x，只有这样，在求f_x时g(y)才能等于0。

综合示例

示例1

　　判断平面向量场是否是保守场：

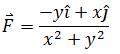
　　保守场的前提是，场处处有定义且处处可导，这里的场在x = y = 0处没有定义，所以可以直接判定不是保守场。

　　也可以费点力气验证，C是单位圆：

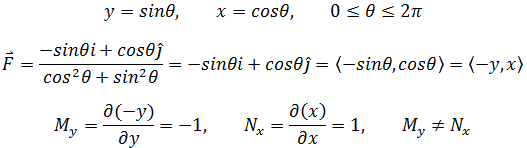
　　所以F不是保守场，如果绕单位园一周：

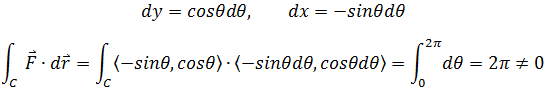
示例2

　　向量场中b是一个常数，

 

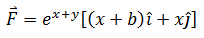
　　当b = ? 时该向量场是一个梯度场？梯度场的势函数是什么？

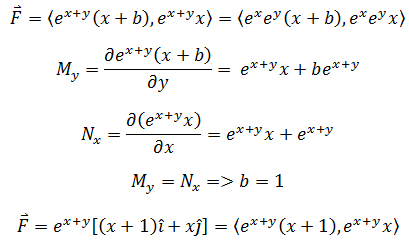
　　线积分法求解势函数：

　　不定积分法求解势函数：

 

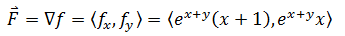
　　选用f_y求y的积分,因为看起来更简单一点：

 

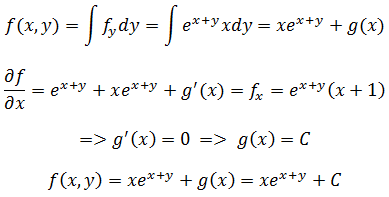
　　可以看到，不定积分法要比线积分法更有效率。

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”