参数方程的示例
现在有两个函数,x = acost和y = asint,如果将t看作时间,我们感兴趣的第一个问题是这两个函数将形成什么曲线?
x2 + y2 = a2cos2t + a2sin2t = a2
很明显是一个圆。
另一个关注的问题是随着时间t的变化,在这个圆上的运动方向,包括什么时间上位于圆的哪个位置,可以把它想象成行星的轨道。
可以通过描点解决。
t = 0, (x, y ) = (acos0, sin0) = (a, 0)
t = π/2, (x, y) = (acosπ/2, sinπ/2) = (0, a)
t = π, (x, y) = (acosπ, sinπ) = (-a, 0)
t = 3π/2, (x, y) = (acos3π/2, sin3π/2) = (0, -a)
由此可以得知,点在圆上逆时针运动:

最后一个感兴趣的问题是弧长,也就是在一段时间内移动的路程:
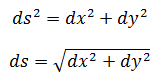
弧长关于时间的变化率:

由此推出:
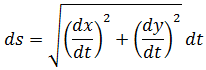
将这个结果应用到上面的问题:

这可以看作是点绕圆运动的速率,由于a是一个常数,所以它是匀速运动的。
如果现在有一个新的速度,x = acoskt,y = asinkt,则:

速度改变了,但运动仍是匀速的。
以上是一个简单的参数方程的推导过程,我们的推导依据是弧长公式:
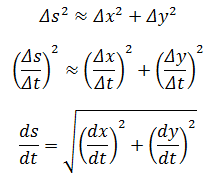
参数方程包含的信息
两个函数x = 2sint,y = cost,根据这两个函数可以得到:
x2/4 + y2 = sin2t + cos2t = 1
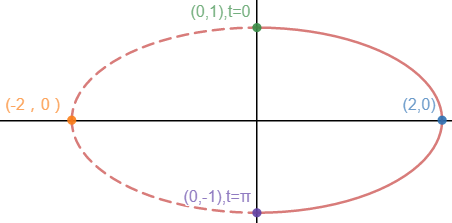
在平面直角坐标系中这是一个椭圆,除此之外还可以得到很多特定的信息,比如起点、轨迹、方向、速率和弧长。
如果去t = 0为起点,则:
t = 0, (x, y) = (0, 1)
t = π/2, (x, y) = (2, 0)
t =π, (x, y) = (0, -1)
t =3π/2, (x, y) = (-2, 0)
点按照顺时针方向走椭圆上运动:

点在一路上的速率:
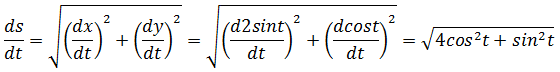
点运行一周需要的时间是2π,需要对ds积分,所以椭圆的弧长:
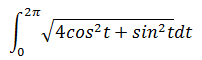
这是一个高等积分了,没有可以用初等函数表示的原函数,所以这就是弧长的答案,也是为什么中学没有学习过椭圆周长公式的原因。
新的思维模式
在上面的例子中,x = 2sint,y = cost,虽然我们最终将它们联合在一起形成直角坐标系中的曲线,但是需要注意的是,这里的x和y分别代表两个不同的函数,我们不再认为y是x的函数,即y ≠ y(x)。这是很明显的,因为同一个x将对应两个y值。此时参数t的作用便凸显出来,通过t建立方程,描述整个曲线。t是没有出现在图像上的另一个维度,所以我们将t想象时间:一个点沿着椭圆跑,在不同的时间到达不同的位置。
在这个例子中,我们要抛开“y是x的函数”的概念,这里y和x都是t的函数,y = y(t),x = x(t),它们有了不同的意义,x不再是自变量,它也是函数。理解了这一点,就可以站在更高的层面看待问题。
椭球的表面积
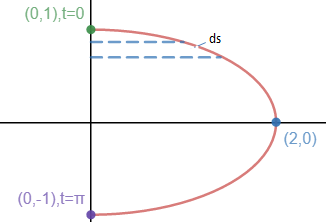
现在需要计算x = 2sint,y = cost形成的椭圆绕y轴旋转,形成的椭球的表面积。
依然使用圆盘法,对弧长ds进行积分:

示例
根据参数方程计算曲线在1 ≤ t ≤ 2时的长度,y = t – 1/t, x = t + 1/t

出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”
