线性近似
假设一般函数上存在点(x0, f(x0))，当x接近基点x0时，可以使用函数在x0点的切线作为函数的近似线。函数f(x)≈f(x0)+f'(x0)(x- x0)即称为函数f在x0点的线性近似或切线近似。
f(x) ≈ f(x0) + f'(x0)(x- x0)
公式来源
导数的定义：
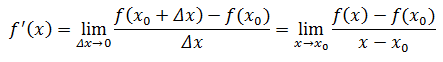
左右两边同时乘以x-x0，并去掉极限符号：
在x≈x0=0时
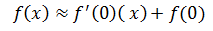
几何意义
线性近似求解的是近似值，其几何意义是在基点的切线近似于原函数的曲线。
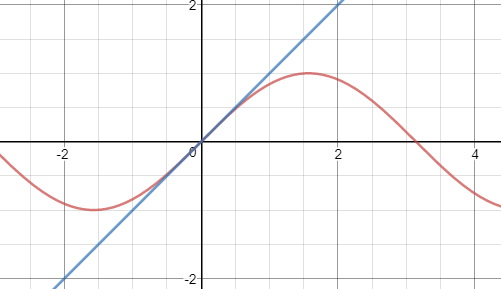
以f(x)=lnx为例，根据公式，在x0=1，lnx≈x-1，曲线和切线如下图所示：
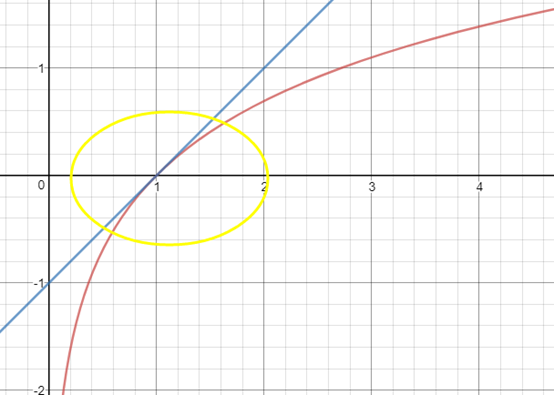
在x0=1点附近，曲线近似于直线，x越接近x0，二者的近似度越高。在讨论近似时，只有指定基点才有意义。这很容易理解，x越远离x0，曲线和直线的差距越大；同时，当基点不同时，切线的斜率也不同。
常用线性近似
x0=0
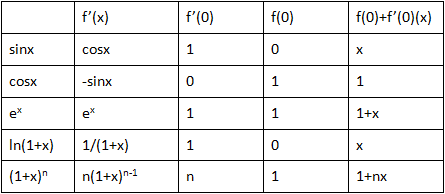
以下是上述线性近似的几何意义：
sinx≈x
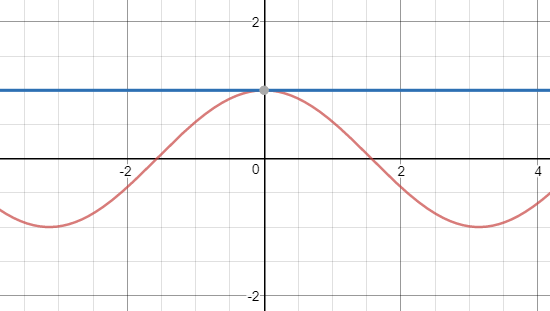
cosx≈1
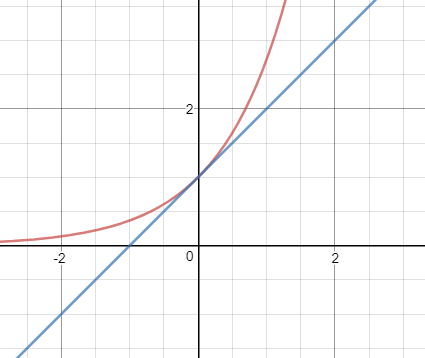
ex≈x+1
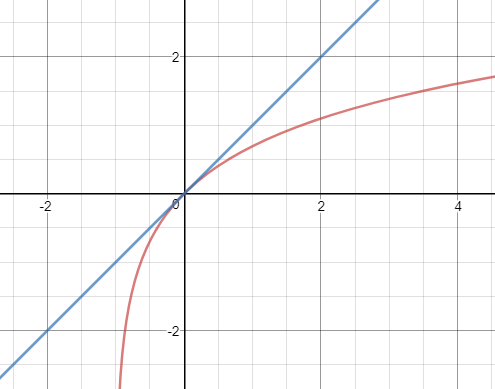
ln(x+1)≈x
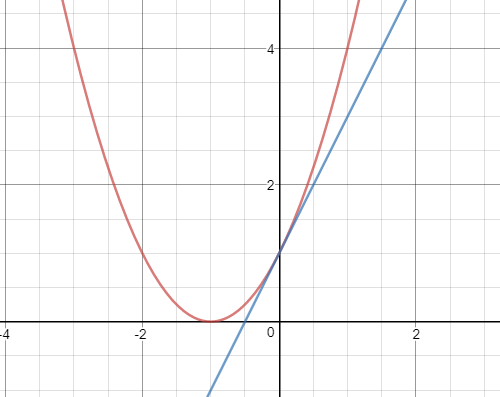
(1+x)n≈1+nx,n=2
化繁为简
例1：ln(1.1) = ?
这需要计算器了，但实际工作中往往只需要寻找近似值。
如果设x=0.1，则 ln(1.1) = ln(1+x)，当x≈0时，ln(1+x) ≈ x，在此， 我们认为0.1接近于0，ln(1.1) = ln(1+x) ≈ x = 0.1
0.1是否接近于0，这是个及其主观的判断，要视具体问题而定。某些时候，0.1可能距离0很远，另一些时候，10也可能距离0很近。
例2：在x≈0时，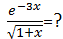
这不需要计算器，直接将代入x=0即可，结果为1。然而这种方法太过简陋，如果判断x=0.1≈0，就需要一个更精确的结果，不能直接将0代入。
还是使用线性近似的思路，首先需要把式子转换成我们认识的写法：
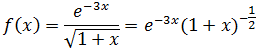
当x≈0时，根据公式f(x) ≈ f'(0)(x) + f(0)，重点是计算f’(0)：
对这个长长的式子求导非常麻烦，涉及到多个求导法则，我们希望用简单的方式求解。
对于本例来说，非常幸运，我们已经知道x≈0时 ex≈1+x，xn≈1+nx，代入本例：
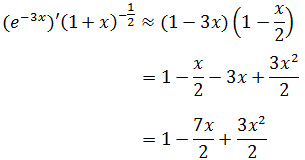
当x≈0时，高阶函数3x2/2≈0，随着x→0，3x2/2更快地趋近于0，所以上式可舍弃高阶函数：
通过这两个例子可以看出线性近似的作用——化繁为简。等号左侧的式子是繁，比如ln1.1和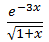
，通过线性近似将其转化为简单的式子，0.1和1-7x/2
在转换过程中当然会损失一些精度，但绝大多数时候我们都无需得到精确的解，例如在x=0.0001的时候，原式的计算量相当大，化简后将极大地简化计算，而付出的代价相当少，几乎可以忽略；某些时候甚至根本无法得到精确解，比如无理数的计算。取而代之，我们求得可接受的近似解，通过近似解化繁为简。
化繁为简的思路也贯穿于整个数学，后续我们将看到，在求解复杂问题时，采取的方法几乎都是不断寻找近似、舍弃。
在利用计算机寻找最优解时，几个常用的算法是爬山法、模拟退火算法、遗传算法，这些算法都是采用化繁为简的思路，舍弃全局最优解，寻找可以接受的较好解，故每次得到的结果都会稍有偏差。
二阶近似
公式
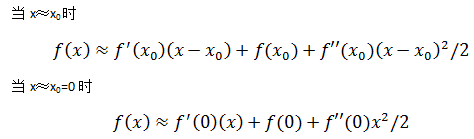
几何意义
二阶近似的几何意义是最接近原函数的抛物线，它比线性近似更为精确。
以f(x)=ln(1+x)为例，根据公式，在x0=0，
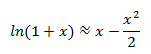
曲线如下：
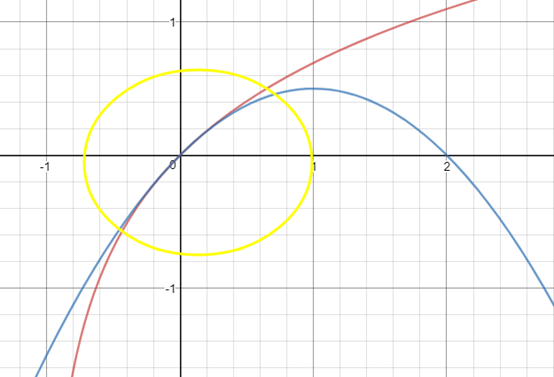
ln(1+x)≈x-x2/2
对比线性近似可以看出，二阶近似在基点附近更贴近原函数。
为什么会出现1/2
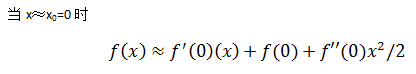
为什么会出现1/2呢？
二级近似的几何意义是最接近曲线的抛物线，如果原曲线本身就是抛物线，则二阶近似就是原曲线本身。
原函数f(x) = a + bx + cx2
f’(x) = b + 2cx
f’’(x) = 2c
当x = 0时，
f(0) = a, f’(0) = b , f’’(0) = 2c
二阶近似 f(x) ≈ a + bx + 2cx2/2 = a + b + cx2
这就是出现1/2的原因，当然，仅当f(x) = a + bx + cx2时才能如此精确。
常用二阶近似
x0=0
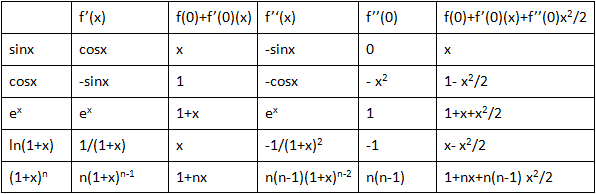
以下是上述线性近似的几何意义：
sinx≈x
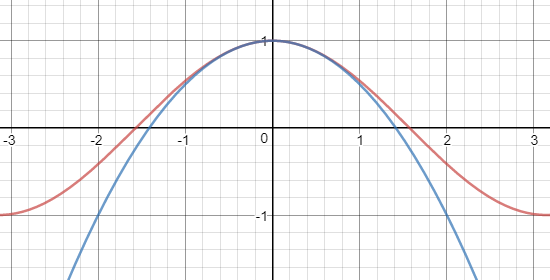
cosx≈1-x2/2
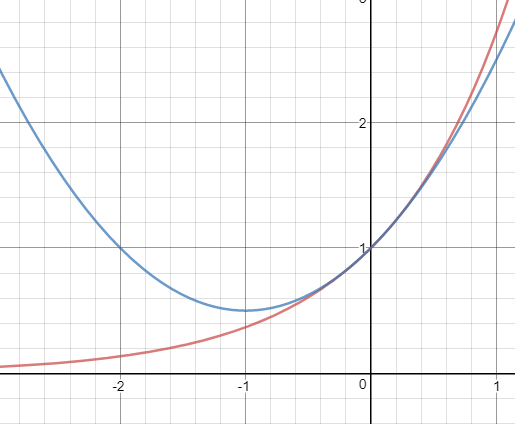
ex≈1+x+x2/2
ln(1+x)≈x-x2/2
示例
在x≈0时，e-3x(1+x)-1/2=?
根据ex≈1+x+x2/2 和 (1+x)n≈1+nx+n(n-1) x2/2
e-3x(1+x)-1/2≈(1-3x+(-3x/2)2)(1-x/2+(-1/2)(-3/2)x2/2)
舍弃3阶和4阶函数，e-3x(1+x)-1/2≈1-7x/2+51x2/8
总结
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
