单变量微积分笔记5——导数5（指数函数和对数函数的导数）

 指数函数的性质

　　先来复习一下中学的课程：

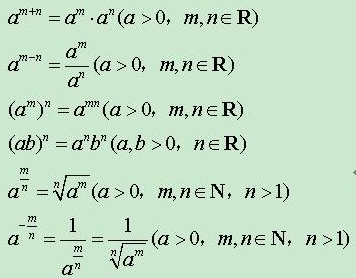
指数函数的导数

　　对f(x) = a^x求导：

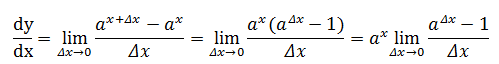
　　a^x右侧的那个极限似乎没有办法继续简化了，如果这个极限看作关于a的函数（之所以将极限看作关于a的函数，是因为在这个极限中，a是未知的，Δx是已知的）：

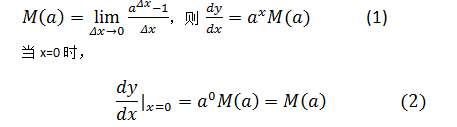
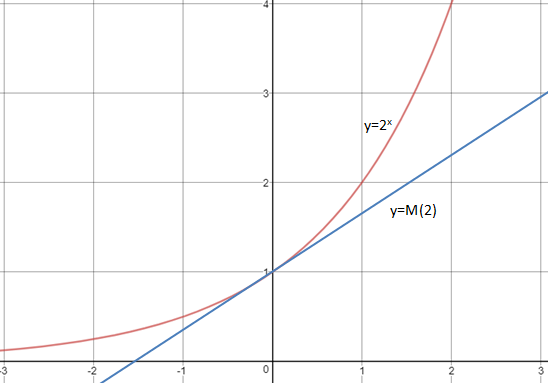
　　函数在某一点导数的几何意义是该点处切线的斜率，所以M(a)也就是ax在x=0处切线的斜率。

　　如果y=2^x，则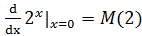，我们仍不知道M(a)是什么，暂且作为悬念。

e

　　我们知道e表示自然对数的底数，暂且不管自然对数到底是什么，只知道它确实存在。e有两个性质：

　　1) (e^x)’ = e^x

　　2) e^x在x=0的导数是1

　　当我们想要继续对f(kx)=2^kx，k∈R求导时，根据上节的公式（2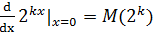），，这并没有解决问题，看起来更复杂了。如果已知函数某一点的导数，就能求得该函数压缩或伸展后在该点的导数，2^kx仅仅是2^x的压缩或伸展，在x=0处的斜率也不断向左或向右倾斜：

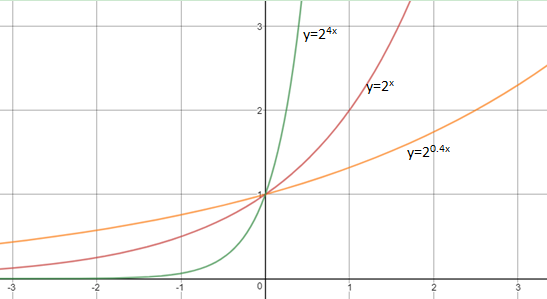
　　当k=1/M(2)时，(b^x)在x=0处的导数是1，b = e，虽然暂时不知道它的值，但已经知道它确实存在。

对数的性质

自然对数的导数

　　自然对数是以e为底的对数，简写做ln

　　

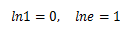
　　y=lne和y=e^x互为反函数：

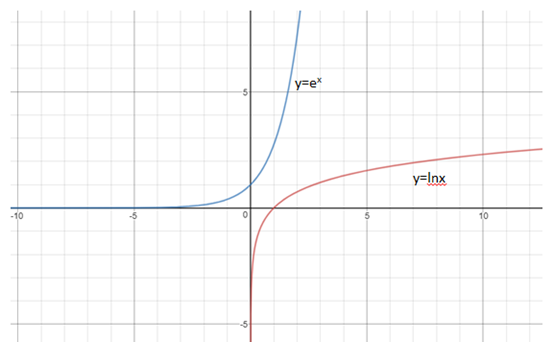
lnx求导

　　对于函数y = lnx，其反函数是e^y = x，根据反函数微分法：

M(a)的真相

　　已经做了足够多的准备工作，是时候揭开M(a)的真相了。

　　在对指数函数y=a^x求导时，我们得出(a^x)’=a^xM(a)。根据对数的性质，e^lna = a，原函数需要使用对数进行一次变换：

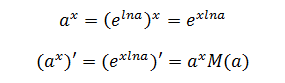
　　根据链式求导法则，

　　所以，M(a) = ln(a)

指数函数的求导公式

　　由于已经知道了M(a)，所以我们终于可以完成对指数函数的求导了。

　　对数函数求导公式：(a^x)’ = a^xlna

 　　示例：

　　(10^x)’ = 10^xln10， (2^x)’ = 2^x ln2

对数微分法

　　自然对数求导公式：(lnu)’ = u’/u，u是x的函数

　　根据该公式，(lnx)’ = x’/x = 1/x

 

　　示例1：(lnx)’ = x’/x = 1/x

　　示例2：(lna^x)’ = (a^x)’/ a^x = (a^x lna) / a^x = lna

　　示例3：(x^x)’

 　  这个稍微复杂点，不能直接用指数函数求导法则，因为指数也是x，此时需要使用对数做一次转换。

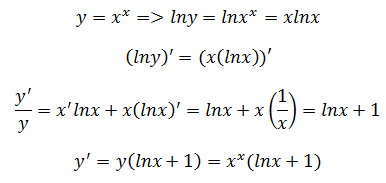
　　示例4：(xⁿ)’

　　根据幂函数求导公式，(xⁿ)’ = nx^n-1，现在使用对数转换对其求解：

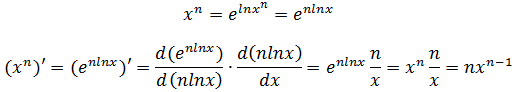
　　也可以使用对数微分法求解：

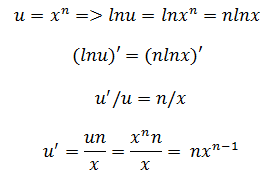
　　示例5：(lnsecx)’

　　(lnsecx)’ = (secx)’/secx = secxtanx/secx = tanx

 e的真相

　　先来看一个极限：

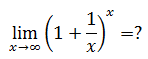
　　这下麻烦了，似乎没有办法直接求解。然而数学的魅力就在于化繁为简，化不可能为可能。暂且抛开lim，并使用对数转换(1+1/x)^x ：

　　由此得出结论：

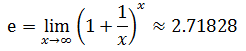
总结

1. (e^x)’ = e，e^x在x=0处的导数是1
2. 指数函数的导数 (a^x)’=a^xlna
3. (lnx)’ = 1/x
4. 对数微分法，(lnu)’ = u’/u
5. 

---

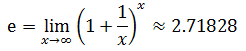
　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”