在对不了解概率的人解释期望时，我总是敷衍地将期望解释为均值。这种敷衍的说法之所以行得通，正是由于大数定律起了作用。
人们在实践中发现，尽管每个随机变量的取值不同，但当随机变量大量出现时，它们的均值却相对恒定，这个规律就是大数定律。
一个公平的骰子
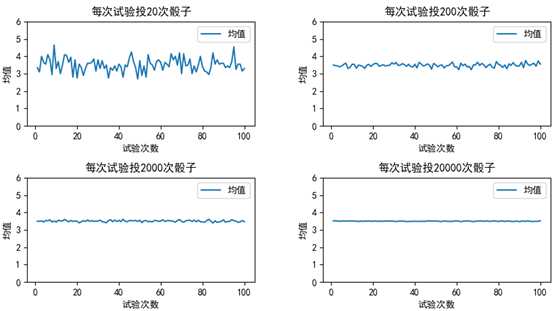
我们有一个公平的骰子，每个点数出现的概率都是1/6，如果只投掷一次，完全无法预测它的点数，但是如果把连续投掷20次看作一次试验，却发现每次试验的点数的均值总是在3.5附近徘徊。每次试验投掷的次数越多，点数的均值越稳定。
import numpy as np import matplotlib.pyplot as plt fig = plt.figure(figsize=(10, 5)) plt.subplots_adjust(hspace=0.5, wspace=0.3) m = 100 # 试验的次数 for i in range(1, 5): n = 2 * 10 ** i # 每次试验投掷n次骰子 mean_list = [np.random.randint(1, 7, n).mean() for i in range(1, m + 1)] # 每次试验的均值 ax = fig.add_subplot(2, 2, i) ax.plot(list(range(1, m + 1)), mean_list, label='均值') plt.yticks(list(range(0, 7))) # 重置y轴的坐标 ax.set_xlabel('试验次数') ax.set_ylabel('均值') ax.set_title('每次试验投{}次骰子'.format(n)) ax.legend(loc='upper right') plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.show()
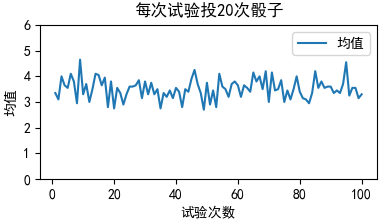
均值的期望和均值的方差
我们用随机变量X1表示第一次投骰子的结果，X2表示第二次……，一个公平的骰子可以得到下面的结论：
连续投掷后将形成一个随机变量序列{ X1, X2, ……, Xn}，这个序列的均值是：
序列中的每个变量都是随机的，因此它们的和及均值也是随机的，也就是说
然是随机的。以n=20为例：
而均值的期望则不同：
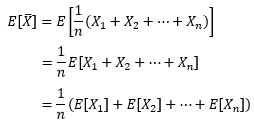
每次掷骰子的结果都是独立同分布的，它们有相同的期望和方差。用μ和σ2表示随机变量的期望和方差，于是我们得到了均值的期望：
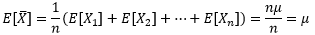
均值的期望等于整体的期望，是一个定值。对于公平的骰子来说，整体的期望与整体的均值相等。
均值的方差是：
辛钦大数定律和伯努利大数定律
n个样本均值的方差是总体方差的1/n，随着n的增大，该方差也越来越小，逐渐趋近于0。方差为0表示随机变量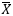
相对于
的波动0，即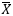不含随机性。换句话说，随着n的增大，样本的均值逐渐收敛于μ，这就是所谓的大数定律。这回有意思了，随着n的增大，作为均值的随机变量居然逐渐变得不含随机性。
这里的大数定律也称为辛钦大数定律或弱大数定律。抄一下教科书上的定义：
设随机变量X1, X2, …, Xn,…相互独立，服从同一分布且具有数学期望E(Xk)=μ(k=1,2,…)，则序列 
依概率收敛于μ，即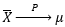
。
样本均值的标准差是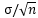
，标准差表示随机变量与总体之间的差异度。想要把差异度缩减10倍，那么n的数量要增加102倍。
伯努利大数定律是辛钦大数定律的一个重要推论。
设fA是n次独立重复试验中事件A发生的次数，p是事件A在每次试验中发生的概率，则对于任意正数ε > 0，有：
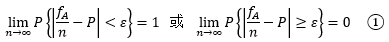
别被定义唬住了，它想解释的问题很简单：当n足够大时，fA/n与P的差值趋近于0，也就是频率趋近于概率，这也是我们用比例估计作为点估计量的基础。在实际问题中，当试验次数很大时，便可以用事件的频率来代替事件的概率。
其实辛钦大数定律也可以用①的方式表示：
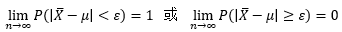
对于概率的符号，有时候有大括号，有时候用小括号，这个还是别太纠结，实际上没什么区别，用大括号只是为了强调事件是一个集合。
不存在的期望
大数定律并不是对所有问题都生效，比如在不存在期望的情况下。
现在我们把骰子换成一枚公平的硬币，参加一个关于硬币第几次正面朝上的游戏。把随机变量X=x看作在第x次投硬币时会得到第1次正面朝上的结果：
如果第1次就得到正面朝上的结果（X=1），得2分
如果第2次才得到正面朝上的结果（X=2），得4分
如果第3次才得到正面朝上的结果（X=3），得8分
……
如果第n次才得到正面朝上的结果（X=n），得2n分
现在我们需要计算得分Y=2X的期望。显然X符合几何分布，每个X又和Y一一对应，因此Y出现的概率等同于X出现的概率：
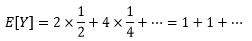
这个期望是发散的，即没法得出具体的数值，也没法求极限，E[Y]=∞表示不存在期望。
蒙特卡罗积分法
假设我们遇到了一个难以计算的积分：
包括换元法、三角替换、分部积分在内的各种方法都无济于事，此时可以求助于暴力的大数定律。
我们知道积分的几何意义是曲线与x轴围成的面积：
曲线f(x)把矩形分割成两部分，U是曲线上方的面积，L是阴影部分的面积，R是整个矩形的面积，是已知量。现在我从们这个矩形内随机选择一点ri=(x, y)，那么根据几何概型，这个点落入L中的概率是L/R。既然积分的是在计算面积L，我们就可以借助积分对落在L中的某一点的概率进行精确的表达：
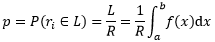
上式同时附带得出积分的结果：
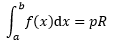
R是已知量，只要求得p，就能得到积分的结果。于是积分问题变成了概率问题。
现在让每个随机点ri都对应一个随机变量Xi，Xi满足下面的特性：
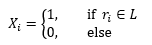
每个随机变量的期望是：
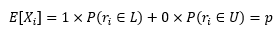
将大数定律应用于Xi上，当n→∞时，Xi的均值依概率收敛于p，即：
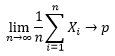
n是落在矩形中的随机点的数量，如果随机点落在L中，Xi=1，否则Xi=0，这个结果实际是告诉我们，当n足够大时，落在L中的点的概率趋近于落在L中点的数量与落在矩形中的总点数的比值。
将这个结果代入积分式：
于是我们可以借助物理实验和计算机的模拟求解这个难以对付的积分。
我们用程序模拟蒙特卡罗积分法，计算下面四分之一圆的面积：
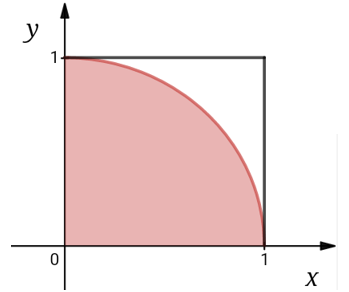
圆的曲线是 x2 + y2 = 1，如果一个随机点(xi, yi)满足x2 + y2 < 1，则表示该点落在了圆内。
import matplotlib.pyplot as plt import numpy as np def create_ri(n): ''' 成 n 个随机点 ''' xs, ys = np.random.random_sample(n), np.random.random_sample(n) # 随机点的横纵坐标 return xs, ys def cnt_circle(xs, ys): ''' 圆中随机点的数量 ''' ps = xs ** 2 + ys ** 2 return ps[ps < 1].size fig = plt.figure() plt.subplots_adjust(hspace=0.5) ax = fig.add_subplot(2, 1, 1) x = y = np.arange(0, 1, 0.001) x, y = np.meshgrid(x,y) ax.contour(x, y, x**2 + y**2, [1]) xs, ys = create_ri(100) ax.scatter(xs, ys, s=10) ax.set_xlabel('x') ax.set_ylabel('y') ax.axis('scaled') xl, yl = [], [] n_max = 10000 for n in range(100, n_max, 10): xs, ys = create_ri(n) cnt = cnt_circle(xs, ys) Area = cnt / n xl.append(n) yl.append(Area) n *= 10 ax = fig.add_subplot(2, 1, 2) ax.hlines(np.pi / 4, xmin=-1000, xmax=n_max + 1000, label='$pi/4$') ax.plot(xl, yl, label='count($r_i$)/n') ax.legend(loc='upper right') ax.set_xlabel('n') ax.set_ylabel('Area') plt.show()
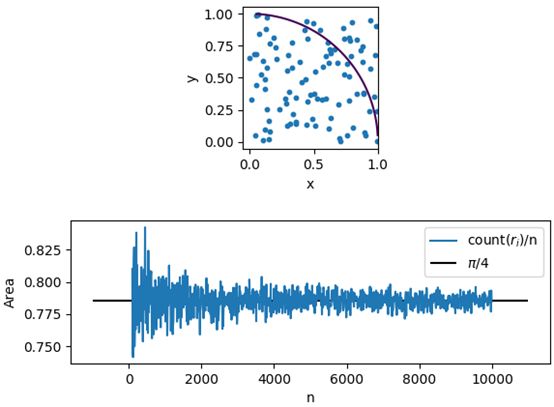
随着n的增加，蓝色曲线的波动越来越小，计算的结果越来越接近真实值。
正像前面提到的，如果想让计算结果的精度提升10倍，需要增加100倍的试验次数，因此蒙特卡罗法的效率并不高。
尽管大数定律下的蒙特卡罗法很好用，但仍然需要小心谨慎，关键之处在于大数定律没有为我们明确指出到底什么才是“大数”，到底需要多少次试验才能充分接近我们所期待的极限。无论n有多大，我们仍然不能否认存在这样的情况：所抛出的硬币全部正面朝上，尽管这种情况发生的概率很小。确定这个概率的方式是中心极限定理的内容。
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
ps = xs ** 2 + ys ** 2
return ps[ps < 1].size