最小公倍数
就像硬币的正反两面,最大公约数往往是和最小公倍数成对出现的。对于两个不等于零的整数a和b,如果a|k且b|k,那么k就是a和b的公倍数;在所有的k中,大于0的最小者就是a和b的最小公倍数(least common multiple),记作c = LCM(a,b),根据惯例,a≥b。
寻找最小公倍数
寻找两个数的最小公倍数远比寻找它们的最大公约数简单:
1 # 求a,b的最小公倍数 2 def lcm(a, b): 3 m, n = abs(a), abs(b) 4 if m < n: 5 m, n = n, m 6 7 result = 1 8 for x in range(1, n + 1): 9 cm = m * x 10 if cm % n == 0: 11 result = cm 12 break 13 14 return result
根据定义,最小公倍数是正整数,计算负数的最小公倍数相当于计算其绝对值的最小公倍数。
寻找最小公倍数2.0版
既然最大公约数和最小公倍数经常成对出现,是否能够通过其中一个直接计算另一个呢?当然可以,这需要用到下面的定理:
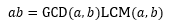
定理说的是a和b的乘积等于它们最大公约数和最小公倍数的乘积,于是我们得到了寻找最小公倍数的另一个版本:
1 # 求a,b的最小公倍数 2 def lcm_2(a, b): 3 m, n = abs(a), abs(b) 4 if m < n: 5 m, n = n, m 6 7 return (a * b) / gcd(a, b)
可以随便找一些数字去验证,验证的结果一定是正确的,但是定理是概念和其它定理推导而来的,而不是根据通过无数个计算总结出来的,让我们看看这个定理为什么成立。
依然是利用素因子表达式:

p1,p2……pt是a和b共同的素因子,它们的次数可以是0,比如:
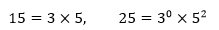
由于素因子分解是唯一的,所以a和b的约数的素因子将是:
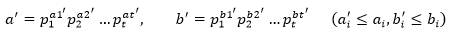
只有这样才能保存a’|a,b’|b。作为a和b的最大公约数,GCD(a,b)可以分解为:
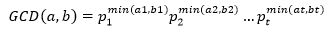
类似的,LCM(a,b)可以分解为:
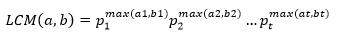
将二者相乘:

哥德巴赫猜想猜的是什么
哥德巴赫猜想是最广为人知的数学难题,它的简称是1+1,这实在不怎么好。最普遍的误解版本是说哥德巴赫猜想就是证明1+1=2——一个苹果加另一个苹果为什等于两个苹果至今还没有被证明,这就一点不贴边了,哥德巴赫才不会那么无聊。另一个误解版本稍微高级一点,说一个素数加上另一个素数等于一个偶数,这个就不用麻烦老爷子了吧,更不用着欧拉,我就能证明。
真正的哥德巴赫猜想是哥德巴赫在1742年提出的:任一大于2的偶数都可写成两个素数之和。但是哥德巴赫自己无法证明它,于是就写信请教赫赫有名的大数学家欧拉帮忙证明,但是一直到死,欧拉也无法证明。因现今数学界已经不使用“1也是素数”这个约定,所以哥德巴赫猜想的现代版本是:“所有大于4的偶数都可以分解成两个素数(质数)的和”,简称1+1,没有=2。

整数比自然数更多吗?
这里有个好玩的问题,整数是无穷的,自然数也是无穷的,那么整数和自然数的个数哪个更多呢?
第一感觉是整数更多,多了一倍,它比自然数多了负值部分。但真相是,二者的数量一样多!这就要了解数学中是怎样定义“一样多”的。在数学中,如果两个集合能够产生一一对应的关系,并且这个对应关系可以用一个函数表示,我们就可以说这两个集合的元素一样多。比如整数和自然数的对应可以是:
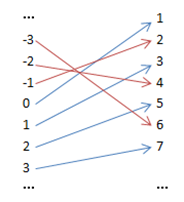
这个对应关系函可以是:

x是整数,f(x)是自然数,无论哪一个整数,都能在自然数中找到唯一的对应。f(x)没有尽头,所以不用关心会对应不上。
自然数和实数是否也有这样的对应关系呢?没有。它们无法产生一一对应,因为每两个实数间都有无穷多个数,无法有效写出一个对应关系。
全体实数比±1之间的实数更多吗?
整数和自然数一样多,那么全体实数的个数与[-1,1]区间内的实数个数哪个多呢?第一感觉又是实数多,但实际上二者一样多!
这个匪夷所思的问题可以用一个数轴表示,说明二者一一对应:数轴上的每一个点都代表一个实数,把-1 到1之间的线段的向上弯折,得到一个与0点相切,弧长是2的圆弧:
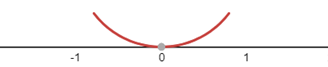
现在,把数轴上的任意点与弧连线,都可以在弧上找到唯一点:

弧上的点和数轴上的点都有无数个,最终的密集连线将会变成一个平面,无限远端的连线也将近似地平行于数轴。由此可见,二者的数量相等,更准确的说是“势”相等。
作者:我是8位的
